Ionic Solids

Skills to Develop

• Describe the coordination number and some characteristics of a unit cell
• Relate lattice energy and some of the properties of ionic solids

Ionic solids are made of lattices of alternating ions. They can't be close-packed structures, because then like ions would have to touch. We've already seen 2 common ionic unit cells: the CsCl structure and the NaCl structure, on the lattices page. We'll show a few more below, but first, let's talk about interpreting unit cells a little more.

Interpreting Unit Cells

When you look at a unit cell, it's good to be able to figure out what the coordination number of each atom is, and what the overall formula is. When you do this, you need to remember that the unit cell repeats. So to count the number of atoms of each type in the unit cell, we have to count the atoms at the corners as 1/8, the atoms on edges as 1/4, and the atoms on faces as 1/2. The rest of these border atoms are in other cells. When you count coordination number, you also have to remember that atoms might have neighbors in other cells. Here's a formula that can help you:

\[\frac{number\; of\; cations\; per\; unit\; cell}{number\; of\; anions\; per\; unit\; cell} = \frac{anion\; coordination\; number}{cation\; coordination\; number}\]

The key thing is that the number of cations and anions in the unit cell is the same as the overall formula, and, for example, if the formula is AB₂, then the coordination number of A is double the coordination number of B.

Unit Cells for Ionic Crystals

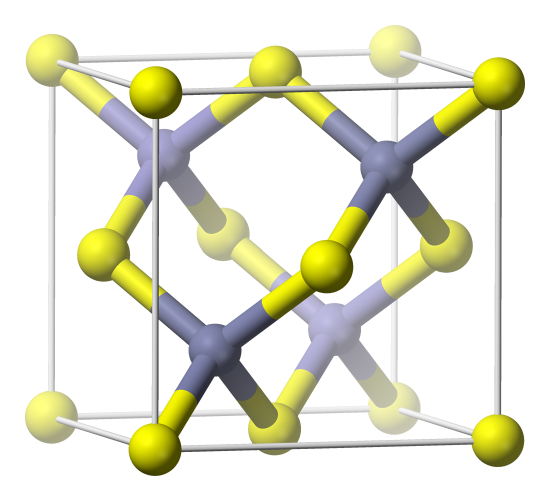
In addition to the ones we saw before, a common structure for the formula AB is called the zinc blende or ZnS structure. Let's analyze this unit cell as shown below. We can see that the grey ions have tetrahedral coordination, and there are 4 of them inside the unit cell. What is the coordination number of the yellow ions, and how many of them are there? It might be a little hard to answer the first question. Let's count them first: each corner has a yellow ion, but since they are on corners, 8 x 1/8 = 1. Then there is a yellow ion on each face of the unit cell, and there are 6 faces. 6 x 1/2 = 3. So there are 4 yellow ions inside each unit cell. This is the same as the number of gray ions, so the formula is AB, as we said. Since the formula is AB, the coordination number of the yellow ions must also be 4. Try to convince yourself that this is true. If you think about each of the corner positions as the same (each corner atom has the interactions of all the corners added together) you can see that they also have tetrahedral coordination.

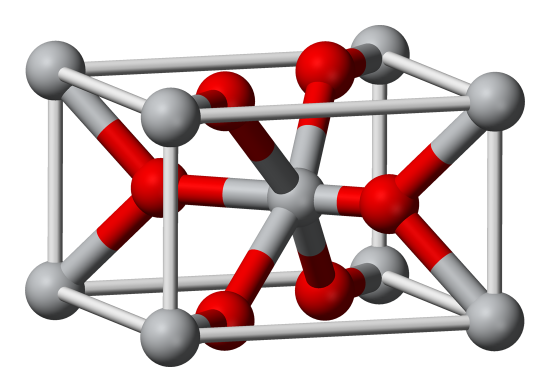
Let's look at an example of an AB₂ structure. Below is the rutile structure, which is quite common, and occurs in many materials including the very common TiO₂, which is used in everything from sunscreen to paper to paint. Let's analyze this one also. In the rutile structure, we have a red ion on each corner and one in the middle, so that's 2 red per unit cell. Then we have 2 gray in the middle and 4 on faces (it's a little hard to be sure they're on the faces from the picture, but they are), so that's 4 gray ions total. The formula is AB₂. What are the coordination numbers? The gray in the middle is clearly octahedral (6-coordinate). The gray on the corners is also octahedral. If we consider all the interactions between the corners and the inside of the cell, we have 4 bonds to reds that are fully inside, and 4 bonds to reds on faces. We have to count the reds on faces as 1/2, so the coordination number is still 6 for the corners. We can count the red coordination number as 3 easily for the middle, and as 3 for the reds on faces also if we are careful. This fits the equation.

There are many, many other structures. Some are very regular and symmetric, and some are distorted. Some structures are more complex to fit more complex formulas. We don't need to worry about the others now. If you are curious why some materials have one structure and some have another, there are 2 main effects to consider. First, it depends on the relative sizes of the ions. If the ions are similar sizes, the CsCl structure is good, because it has the highest coordination number (more favorable interactions between opposite ions). If the ions aren't the same size, then in the CsCl structure the big ions might touch each other, so the NaCl structure (with coordination number 6) becomes more stable, so the big ions can be farther apart. For even less equal sizes, the zincblende structure might be necessary. The other effect is how covalent the bonds are. If the bonds are partly covalent, even if the sizes aren't so different, the zincblende structure might be better because it allows better orbital overlap (just like in diamond, which has the same structure but with all the atoms the same).

Properties of Ionic Solids

Ionic solids are usually insulators, because electrons are held tightly to the ions. They are hard and have high melting points, because ionic bonds are strong. However, they are brittle because if the crystal gets knocked so that the wrong ions are touching, it will shatter.

A key concept for ionic bonding is the lattice energy. If you compare the electron affinity for a non-metal and the ionization energy for a metal, you'll notice that forming ions is endothermic. However, remember that electron affinities and ionization energies are defined for gases. Making ionic solids from the elements is very exothermic, because bringing the ions together into the crystal lattice is releases a lot of heat. The lattice energy is the energy released when the solid forms from ions in the gas phase. The lattice energy includes all the ion-ion interactions in an infinite lattice, so it is a little complicated to calculate. The main thing to know is that the smaller the ions and the larger the charge, the bigger the lattice energy is, and the more stable the solid.

An illustration of lattice energy (ΔH₁).

Contributors and Attributions

• Emily V Eames (City College of San Francisco)