9.18: Deviations from the Ideal Gas Law

Figure \(\PageIndex{1}\) Plot of PV versus P for methane (CH₄) gas at three temperatures.

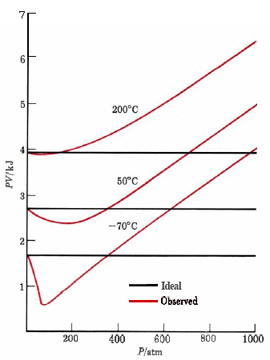
Sufficiently accurate measurement of pressure, temperature, volume, and amount of any gas will reveal that the ideal gas law is never obeyed exactly. This is why the molar volumes in Table 1 from Avagodro's Law were not all exactly 22.414 liters. A convenient way to detect deviations from the ideal gas law is to calculate PV under various conditions. According to the kinetic theory, PV is two-thirds the total molecular kinetic energy and should remain constant at a given temperature for a given amount of gas. That it does not is evident from Figure \(\PageIndex{1}\), where PV for 1 mol CH₄(g) is plotted versus P. At high pressures, PV is always larger than would be predicted by the ideal gas law. As the temperature decreases, deviations occur at lower pressures, and PV drops below the predicted horizontal line before rising again with pressure.

At high pressures, PV increases above the ideal gas value because the first postulate of the kinetic theory of gases is no longer valid. As pressure increases, the molecules are squeezed close to one another, and the volume of the molecules themselves becomes a significant fraction of the volume of the container. This is shown in Figure \(\PageIndex{2}\). The space which other molecules are prevented from occupying is called the excluded volume. The measured volume of the container, V_container, is the sum of the volume available to the gas molecules, V_gas, and this excluded volume. Since PV_container is larger than PV_gas, the experimentally measured PV is too large.

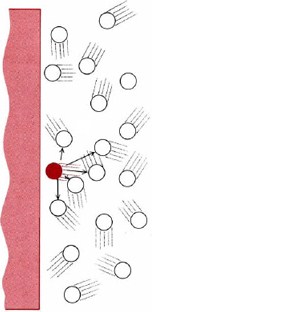
Intermolecular forces cause PV to drop below the ideal gas prediction at low temperatures and medium pressures. Consider a gas molecule which is about to hit the wall of the container (Figure \(\PageIndex{3}\) ). Kinetic theory assumes that its neighbors exert no forces on such a molecule except during a collision (postulate 5), but we know that such forces exist.

Figure \(\PageIndex{2}\) The excluded volume. Because the molecules in a gas have a finite volume, they are not free to move about throughout the whole volume of the container. The figure represents the molecules (black) stationary at a given instant of time. If we added a new molecule to the gas, its center would have to be in the volume colored red. The white and black volumes together are called the excluded volume. Note that the excluded volume is larger than the actual volume of the molecules.

When a molecule is near the wall, the attractions between it and its neighbors are unbalanced, tending to pull it away from the wall. The molecule produces slightly less impact than it would if there were no intermolecular forces. All collisions with the walls are softer, and the pressure is less than would be predicted by the ideal gas law. This effect of intermolecular forces is more pronounced at lower temperatures because under those conditions the kinetic energies of the molecules are smaller. The potential energy of intermolecular attraction is comparable to that kinetic energy and can have a significant effect.

Figure \(\PageIndex{3}\) The effect of intermolecular forces on the pressure of a gas. A molecule about to hit the wall, such as the one indicated in red, is held back by the attractive forces of its fellow molecules and strikes the wall with less impact than would have been the case if these forces were absent.

For gases such as hydrogen, oxygen, nitrogen, helium, or neon, deviations from the ideal gas law are less than 0.1 percent at room temperature and atmospheric pressure. Other gases, such as carbon dioxide or ammonia, have stronger intermolecular forces and consequently greater deviation from ideality. Nonideal behavior is quite pronounced for any gas at very high pressures or at temperatures just above the boiling point. Under these conditions molecular volume or intermolecular attractions can have maximum effect.