8.6: Alkanes
- Page ID
- 49427
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Most of the hydrocarbons in petroleum belong to a family of compounds called the alkanes, in which all carbon atoms are linked by single bonds.
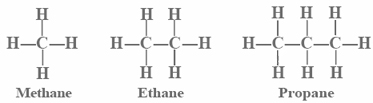
Ball-and-stick models of alkane molecules which contain up to three carbon atoms are shown in Figure \(\PageIndex{1}\). Methane (a) has four C—H bonds arranged tetrahedrally around a single carbon atom. Ethane (b) has a slightly more complicated structure—each carbon is still surrounded tetrahedrally by four bonds, but only three are C―H bonds, while the fourth is a C—C bond. Ethane may be thought of as two methyl groups connected by a single C—C bond. (The methyl group, CH3—, has the same structure as methane except that one hydrogen has been removed.) Thus the formula for ethane is CH3CH3 or C2H6.
The third member of the alkane family is propane. As can be seen in part c, the three carbon atoms are in a chain. The two methyl groups at the ends of the chain are linked together by a methylene group, —CH2—. The formula is CH3CH2CH3 or C3H8. Again the tetrahedral arrangement of C—H or C—C bonds around each carbon atom is maintained.
Most of us lack the artistic skill to make good three-dimensional sketches of the molecular structures of alkanes or other organic compounds. Consequently projection formulas, which indicate how the atoms are connected but do not show tetrahedral angles of 109.5°, are commonly used. Projection formulas for the three members of the alkane family are
Clearly we could go on to chains of four, five, six, or more carbon atoms by adding more methylene groups to the propane molecule. The first 10 compounds whose structures may be derived in this way are listed in the following table. They are called normal alkanes or straight-chain alkanes, indicating that all contain a single continuous chain of carbon atoms and can be represented by a projection formula whose carbon atoms are in a straight line.
| Name | Molecular Formula | 3D Model | Condensed Structural Formula | Boiling Point (°C) |
|---|---|---|---|---|
| Methane | CH4 |  |
CH4 | -162 |
| Ethane | C2H6 | 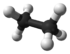 |
CH3CH3 | -89 |
| Propane | C3H8 | 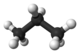 |
CH3CH2CH3 | -42 |
| n-Butane | C4H10 | 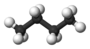 |
CH3(CH2)CH3 | -0.5 |
| n-Pentane | C5H12 | 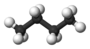 |
CH3(CH2)3CH3 | 36 |
| n-Hexane | C6H14 | 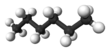 |
CH3(CH2)4CH3 | 69 |
| n-Heptane | C7H16 | 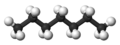 |
CH3(CH2)5CH3 | 98 |
| n-Octane | C8H18 |  |
CH3(CH2)6CH3 | 126 |
| n-Nonane | C9H20 |  |
CH3(CH2)7CH3 | 151 |
| n-Decane | C10H22 |  |
CH3(CH2)8CH3 | 174 |
* The n before the name indicates that this is the normal straight-chain isomer.
Note that all the projection formulas in the table have an initial hydrogen atom followed by a number of CH2 groups. The chain ends with a second single hydrogen atom. The general formula H(CH2)nH, or CnH2n+2, may be written, where n is the number of CH2 groups, or the number of C atoms. Propane, for example, has n = 3. Its formula is C3H8 and it is referred to as a C3 hydrocarbon.
Branched Chains and Isomers
Another important feature of molecular structure is illustrated by the C4 hydrocarbons. In addition to the straight chain shown for normal butane, a branched chain, in which some carbon atoms are linked to more than two other carbons, is possible. The projection formula for the branched-chain compound 2-methylpropane (also called isobutane because it an isomer of butane) is

Unlike normal butane, which has a straight chain of four carbon atoms, the longest chain in isobutane is only three carbon atoms long. The central of these three atoms is bonded to the fourth carbon. Nevertheless, you can verify from the projection formulas or from the ball-and-stick drawings that both normal butane and isobutane have the same molecular formula, C4H10. The two compounds are isomers, just like ethyl alcohol and dimethyl ether, hence the prefix iso in the name for one of them. Just as was mentioned with ethyl alcohol and dimethyl ether, n-butane and isobutane differ in physical properties. Isobutane, being more compact, has smaller London Force interactions than n-butane. Thus it has a lower boiling point. The boiling points can be compared in the table of organic compound boiling points. One should note from this table that of all the organic compounds to consider, alkanes, both straight chained and branched, have the lowest boiling points comparatively.
As the number of carbon atoms in an alkane molecule increases, so do the possibilities for isomerism of this kind. There are three isomeric pentanes, all with the formula C5H12, five isomeric hexanes, C6H14, and nine isomeric heptanes, C7H16. The number of possible isomers of tetracontane, C40H82 is larger than 62 million. Thus an inconceivable variety of different molecular structures is possible for compounds containing only carbon and hydrogen atoms connected by single bonds. In crude oil, the most important source of hydrocarbons in the United States, branched-chain and straight-chain alkanes are about equally common.
Another aspect of the behavior of alkane molecules (and other molecules containing single bonds) is not apparent from ball-and-stick illustrations or from projection formulas. Like small children, molecules cannot stop wriggling, and most alkane structures are not rigid. Groups on either side of a carbon-carbon single bond are able to rotate freely with respect to each other. Rotation of one methyl group with respect to the other in ethane, CH3CH3, is shown in Figure \(\PageIndex{3}\). While there is free rotation around the carbon bond, certain positions are more stable than others. For the ethane molecule is most stable when the hydrogen atoms on one methyl group are offset from those on the other methyl group(referred to as staggered) and more energy is needed to pass through the eclipsed formation, where the hydrogen atoms of both methyl groups line up. Because of this free rotation, and because they collide with other molecules, alkane molecules are constantly flexing and writhing about their C―C bonds, assuming different shapes (different conformations) all the time. Some feeling for the way in which alkane molecules can adopt a variety of conformations is obtained from the following example.

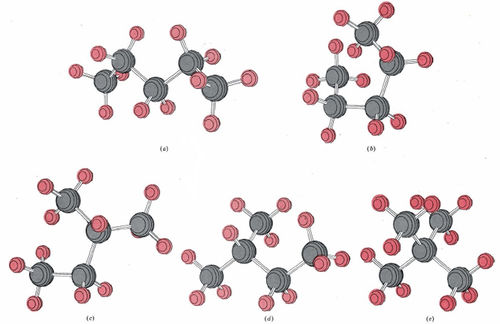
In Figure \(\PageIndex{4}\), five ball-and-stick diagrams labeled (a) through (e) are shown. All five correspond to the formula C5H12 (pentane). Since there are only three isomers of pentane, some of these molecules must correspond to different views or different conformations of the same molecule. Decide which of these diagrams correspond to the same isomer, and which isomer each represents. Draw a projection formula for each isomer.
Solution
Molecule (a) has five carbon atoms in a single continuous sequence. It corresponds to

Careful inspection of (b) reveals that again the five carbon atoms form a single chain. No carbon atom is joined to more than two others. Molecule (b) is thus also n-pentane, but in a different conformation. Molecule (c) does have a carbon atom joined to three others. The longest chain is four carbon atoms long, and an additional carbon atom is attached to the second carbon atom. The projection formula is accordingly
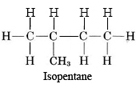
Molecule (d) is also isopentane, while molecule (e) corresponds to the third isomer, called neopentane: