3.3.1: Cultural Connections- Anthropology and Protein Stoichiometry
- Page ID
- 50724
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We have examined the idea of amino acid complementarity, where different foods in the diet supply the correct balance of amino acids to construct Human protein, in another section. Human proteins require stoichiometric amounts of about ten "essential" amino acids, so if only one is missing, the protein cannot be synthesized, and protein malnourishment results. This illustrates the concept of a "limiting reactant", which is a reactant present in less than the stoichiometric amount relative to other reactants.
A diverse group of surviving cultures worldwide have adopted diets, different as they may be, that supply the correct amino acid balance[1]. Anthropologists believe that fortuitous adoption of these diets provided survival value for the cultures. In areas where food is scarce, cultures that do not adopt diets with correct amino acid balance may not survive. Here are some examples of diets that supply approximately the correct stoichiometric amounts of amino acids:
Tostadas
In Latin America, diets combining corn tortillas or other corn products with beans, like the tostada shown here, are common.

Tostada with corn tortilla, bean topping, and vegetables[2]
Beans eaten alone provide limiting amounts of sulfur containing amino acids like methionine and cysteine, so these amino acids limit the amount of Human protein that can be synthesized. Beans have large amounts of the amino acids lysine and tryptophan, so these are "excess reactants" when used to synthesize Human protein, and will be degraded to urea and wasted. If wheat, rice, or corn are eaten alone, they typically provide amounts of lysine and tryptophan which limit the amount of Human protein that can be synthesized. But if beans are eaten with grains or corn, the excess reactants of the beans complement the limiting reactants of the grain (and vice versa). Human protein can then be synthesized efficiently, and very small amounts of amino acids are simply excreted as urea.
The origins of this diet are ancient. The Tehuacan Archaeological-Botanical Project (1961–1964) investigated the beginnings of agriculture in the New World and the concomitant rise of autochthonous (indigenous) civilization [3]. The project is described in six volumes, the first of which explores subsistence and the environment [4]. The domestication of maize after 8000 B.C.E. and beans (3000–4000 B.C.E.) in the Tehuacan Valley (the “Valley of Mexico”) of south central Mexico, gave inhabitants a nutritional advantage in the face of progressively deteriorating resources. Maize cob size increased rapidly under domestication from only a centimeter or two to current size, while Phaseolus vulgaris (kidney and pinto beans) similar to modern ones probably existed in preagricultural times. “Wherever these two food crops met, an immediate adaptive combination favored by human selection was formed.”[5].
Falafel and Pita
In the Middle East, a meal may consist of falafel and hummus made from chickpeas eaten with pita bread made from wheat.
|
Pita with humus and falafel balls[6] |
Dal (lintil soup) Bhat (grain or maize)[7] |
Dal and Chapatis
In India, rice or chapatis are eaten with dal (lentils) to provide amino acid balance.
Corn Deficiencies
We'll invesigate experiments dealing with corn, and the protein malnutrition that can result if it's eaten alone. It's well known that corn is a poor protein food by itself, being low in lysine and tryptophan [8], and even more so when it is nixtamalized. These deficiencies motivated researchers to develop the QPM (Quality Protein Maze) to increase concentrations of these essential amino acids in its protein.
Experiments on rats, whose amino acid requirements are similar to Humans', provide a basis for some stoichiometric calculations [9]. As the table below shows, there was little weight gain improvement when LYS or TRP were added separately to a "Base" diet. That means that neither alone is a limiting amino acid, preventing by itself the synthesis of rat protein. But when both were added, a significant increase was measured, along with a decrease in serum urea. That means that both were limiting, and when both were added, much less amino acid was wasted. The amino acids went into protein synthesis, rather than being simply metabolized and excreted as urea. While the addition of isoleucine in diet 5 made little difference (so it must be supplied adequately by corn), the addition of threonine (THR) alone to Diet 4 increased body weight gain, so it must be limiting in a diet of corn + LYS + TRP. Addition of ILE, methionine (MET), histidine (HIS) and valine (VAL) finally constitutes a nearly balanced diet, as evidenced by the large weight gains and low serum urea in Diet 8.
| Diet | weight gain g/day |
Serum Urea mg/100 mL |
|---|---|---|
| 1. Basea | 1.75 | 36.2 |
| 2. Base + LYS | 1.53 | 36.0 |
| 3. Base + TRP | 1.56 | 42.3 |
| 4. Base + LYS + TRP | 2.62 | 25.8 |
| 5. Diet 4 + ILE | 2.49 | 24.9 |
| 6. Diet 4 + THR | 3.29 | 20.4 |
| 7. Diet 4 + ILE + THR | 4.20 | 23.7 |
| 8. Diet 7 + HIS + MET + VAL | 5.95 | 7.4 |
| 9. Corn + Soybean meal | 6.75 | 38.5b |
aThe base diet consisted of 920.2 g corn, 30.0 g corn oil, 35.0 g mineral mix, 10 g vitamin mix, 2.5 g limestone, and 2.3 g choline. b This large increase is due to the doubling of total dietary protein, rather than protein inefficiency.
The same paper[10] provides the sequence, from most limiting to least, of the amino acids in corn, and the requirement of the rat (similar to Human) published by the NRC[11]. We've added the amino acid amounts in lentils to represent beans[12]
| Amino Acid | Requirement (g/kg) |
Amount in corn (g/kg) |
Amount in lentils (g/kg) |
|---|---|---|---|
| Lysine (LYS) | 7.0 | 2.4 | 6.3 |
| Tryptophan (TRP) | 1.5 | 0.7 | 0.81 |
| Methionine (MET) and Cysteine (CYS) |
6.0 | 3.8 | 0.77 + 1.18 |
| Histidine (HIS) | 3.0 | 2.0 | 2.54 |
| Valine (VAL) | 6.0 | 4.6 | 4.48 |
| Isoleucine (ISO) | 5.0 | 3.9 | 3.90 |
| Threonine (THR) | 5.0 | 3.9 | 3.23 |
| Arginine (ARG) | 6.0 | 5.0 | 6.97 |
| Phenylalanine (PHN) and Tyrosine (TYR) |
8.0 | 9.6 | 4.45 + 2.41 |
| Leucine (LEU) | 7.5 | 11.0 | 6.54 |
How Amino Acids Form Proteins
Amino acids are joined by a very simple "condensation" reaction where two molecules join by eliminating water, as shown in the figure below. The portion of the molecule labeled "R" stands for a variable part of the molecule that distinguishes different amino acids; the rest of the molecule is common to all amino acids.
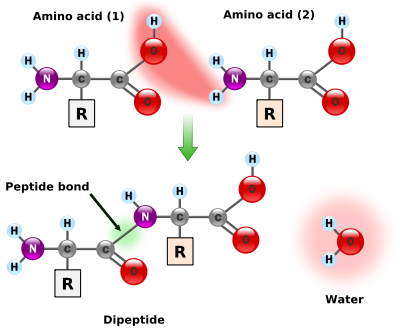
Formation of a peptide bond [13]
This process can continue with different amino acids adding to either end of the protein chain. The H-N of an amino acid adds to the C-OH end of the protein, eliminating water (H-OH) and forming a C-N bond where the water was eliminated (or the C-OH end of an amino acid adds to the N-H end of the protein). This process continues until the protein has hundreds of different amino acids.
Example 1: Stoichiometry of Corn Malnutrition
a. Correct, or Stoichiometric Amino Acid Ratios:
From data in the Table II above, calculate the optimal molar ratio of lysine (LYS, C6H14N2O2, Molar mass 146.19 g/mol) to Arginine (ARG, C6H14N4O2, Molar mass 174.2 g/mol) in the diet.
b. Limiting Amino Acid:
From data in the Table above, calculate which, LYS or ARG, is the limiting reactant in a corn diet?
c. How much of the excess amino acid will be wasted in 1 kg of corn diet?
Solution
a. The balanced equation will have coefficients that we need to determine:
x LYS + y ARG + other amino acids → Protein + water
According to the atomic theory, x mol LYS is required for each y mole of ARG to make useful protein. If the diet is optimal when 7.0 g of LYS is eaten with every 6.0 g of ARG (this ratio might be provided by eggs, for example), we can calculate the optimal stoichiometric ratio:
\(\text{n}_{\text{LYS}}=\text{7.0 g}\times \frac{\text{1 mol LYS}}{\text{146}\text{.19 g}}=\text{0}\text{.048 mol LYS}\)
\(\text{n}_{\text{ARG}}=\text{6.0 g}\times \frac{\text{1 mol ARG}}{\text{174.2 g}}=\text{0}\text{.034 mol ARG}\)
The ratio is \(\frac{\text{LYS}}{ARG}~=~\frac{0.048}{0.034}~=~ \frac{1.4}{1}\)
And since 1.4 is about 1-2/5 or 7/5,
\(\frac{\text{7/5}}{1}~=~ \frac{7}{5}\)
This exact amino acid ratio may not be found in any particular rat protein, but it is the average ratio for all the proteins in the rat. The (partial) chemical equation is
-
- 7 LYS + 5 ARG + other amino acids → Protein + water
That is, the stoichiometric ratio S(LYS/ARG) = 7 mol LYS / 5 mol ARG.
b. Let's see what the mole ratio is in the corn diet.
\(\text{n}_{\text{LYS}}=\text{2.4 g}\times \frac{\text{1 mol LYS}}{\text{146}\text{.19 g}}=\text{0}\text{.016 mol LYS}\)
\(\text{n}_{\text{ARG}}=\text{5.0 g}\times \frac{\text{1 mol ARG}}{\text{174.2 g}}=\text{0}\text{.029 mol ARG}\)
The ratio is \(\frac{LYS}{ARG}~=~\frac{0.016}{0.029}~=~ \frac{0.55}{1}\)
Clearly, LYS is the limiting amino acid because the ratio initial amounts of LYS to ARG (0.55:1) is much less than the required stoichiometric ratio (1.4 : 1).
General Approach to Limiting Reactant Problems
From the corn diet example you can begin to see what needs to be done to determine which of two reagents, X or Y, is limiting. We must compare the stoichiometric ratio S(X/Y) with the actual ratio of amounts of X and Y which were initially mixed together.
The corresponding general rule, for any reagents X and Y, is
\(\begin{align} & \text{If}~\frac{n_{\text{X}}\text{(initial)}}{n_{\text{Y}}\text{(initial)}}~\text{is less than S}\left( \frac{\text{X}}{\text{Y}} \right)\text{, then X is limiting}\text{.} \\ & \\ & \text{If}~\frac{n_{\text{X}}\text{(initial)}}{n_{\text{Y}}\text{(initial)}}~\text{is greater than S}\left( \frac{\text{X}}{\text{Y}} \right)\text{, then Y is limiting}\text{.} \\ \end{align}\)
Of course, when the amounts of X and Y are in exactly the stoichiometric ratio, both reagents will be completely consumed at the same time, and neither is in excess.
We can verify that LYS is limiting by calculating the amount of LYS that would be required if all the ARG reacted, using a stoichiometric ratio:
\(n_{\text{ARG}}\text{ }\xrightarrow{S\text{(LYS/ARG}\text{)}}\text{ }n_{\text{LYS}}\)
\(\text{0.029 mol ARG}~\times~\frac{\text{7 mol LYS}}{\text{5 mol ARG}}~=~\text{0.041 mol LYS}\)
Similarly, if all the LYS reacts, the required amount of ARG is
\(\text{0.016 mol LYS}~\times~\frac{\text{5 mol ARG}}{\text{7 mol LYS}}~=~\text{0.018 mol ARG}\)
This is much less than the amount present, so ARG is the Excess Reactant.
c. We can easily use the molar masses to convert the amounts of each amino acid to the masses.
Let's set up a table:
| 7 LYS | + 5 ARG | other amino acids → | Protein + water | |
|---|---|---|---|---|
| M (g/mol) | 146.19 | 174.2 | ||
| m (g) | 2.4 | 5.0 | ||
| n (mol)present | 0.016 | 0.029 | ||
| if all LYS reacts | -0.016 | -0.011 | ||
| Remaining amount | 0 | 0.018 | ||
| Remaining mass (g) | 0 | 3.14 |
When the reaction ends, 3.14 g of the original 5.0 g (63%) remains, and will be metabolized to urea and excreted. Of the entire diet of 2.4 g LYS + 5.0 g ARG, we see that 3.14 g or 42% is wasted. What a waste of food and the resources to produce it! Notice that the corn serving will also have to be larger than the serving of optimal diet for the same amount of protein, because corn has only 5 g/kg ARG, while the optimal diet has 6.0 g/kg. The optimal diet might be provided by meat or eggs, but they are environmentally demanding and present health concerns.
Example 2: Complementary Amino Acids
A subsistence bean diet may also lead to protein malnutrition, as inspection of Table II above shows. Although the Lysine content is much greater than in beans, the methionine (MET) and Cystine (CYS) levels are low, as are the Phenylalanine (PHE) and Tyrosine (TYR).
But suppose beans and corn are eaten in the same day, in a diet that mixed equal masses of corn and lentils. Now recalculate the limiting amino acid in a diet of 2.4 + 6.3 = 8.7 g of LYS and 5.0 + 6.97 = 11.97 g of ARG.
b. In this case, how much of the excess amino acid is wasted?
Solution
\(\text{n}_{\text{LYS}}~=~\text{8.7 g}~\times~ \frac{\text{7 mol LYS}}{\text{146.19 g}}=\text{0}\text{.060 mol LYS}\)
\(\text{n}_{\text{ARG}}~=~\text{11.97 g}~\times~ \frac{\text{1 mol ARG}}{\text{174.2 g}}=\text{0}\text{.069 mol ARG}\)
Now we see that the ratio of amounts present is
0.060 mol LYS / 0.069 mol ARG = 0.869,
which is still less than the stoichiometric ratio,
7 mol LYS / 5 mol ARG = 1.4
So LYS is once again the limiting amino acid. Recalculating the values in a table as above, we get
| 7 LYS | + 5 ARG | other amino acids → | Protein + water | |
|---|---|---|---|---|
| M (g/mol) | 146.19 | 174.2 | ||
| m (g) | 8.7 | 11.97 | ||
| n (mol)present | 0.060 | 0.069 | ||
| if all LYS reacts | -0.060 | -0.043 | ||
| Remaining amount | 0 | 0.027 | ||
| Remaining mass (g) | 0 | 4.61 |
In this case, 4.61 g of the excess ARG remains from a 11.97 g portion, or 38% of the ARG. The total diet is 8.7 g LYS + 11.97 g ARG = 20.7 g, and only 22% of that is wasted, a big improvement over the corn alone case above.
In order to design a proper diet, complementary protein foods would have to be chosen from tables of amino acid contents of foods.
Is Nixtamalization an Anthropological Counterargument?
In Central America, field corn or "maize" is traditionally boiled in lime (CaO) to loosen the hulls and soften the kernels in the preparation of tortilla flour. The process is shown beautifully in a Culinary Institute of America film. The Southern US breakfast "grits" are also made this way[14].
But this process converts some of the already limiting tryptophan to 2-aminoacetophenone, exacerbating the poor nutritional, and survival value, of the corn. But the nixtamalization also makes niacin in the kernels more bioavailable, reducing the incidence of Pellagra, and more than offsetting the loss of amino acids if plenty of beans are also included in the diet. The beans & corn diet, even with nixtamalization, has survival value for cultures.
Example 3: Amino Acid Detection
To detect an amino acid (even in a fingerprint in forensic chemistry), the ninhydrin test is often used.
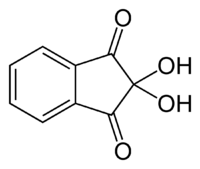
Ninhydrin
In the ninhydrin test, two ninhydrin molecules (C9H6O4, shown to the left) become linked by the N attached to the first carbon of the amino acid chain, producing the blue/purple ion shown at right.
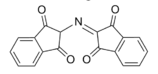
Blue/Purple Product[15]
The balanced chemical equation is:
2 C9H6O4 + C11H12N2O2 → (C9H5O2)-N=(C9H4O2) + C10H9NO + CO2 + 3 H2O
If 2.00 mg of ninhydrin (Nin) is used to detect 2 mg of TRP, has enough ninhydrin been added to react with all the TRP? Which is the limiting reagent, and what mass of H2O will be formed?
Solution
The stoichiometric ratio connecting Nin and TRP is
\(\text{S}\left( \frac{\text{Nin}}{\text{TRP}} \right)=\frac{\text{2 mol Nin}}{\text{1 mol TRP}}\) The initial amounts of Nin and TRP are calculated using appropriate molar masses(160.13 g mol−1 for Nin and 204.23 g mol−1 for TRP: \(\begin{align} & \text{ }n_{\text{Nin}}\text{(initial)}=\text{2}\text{.00}\times \text{10}^{\text{-3}}\text{g}\times \frac{\text{1 mol Nin}}{\text{178}\text{.14 g}}=\text{1}\text{.12}\times \text{10}^{\text{-5}}\text{mol Nin} \\ & \\ & n_{\text{TRP}}\text{(initial)}=\text{2}\text{.00}\times \text{10}^{\text{-3}}\text{g}\times \frac{\text{1 mol TRP}}{\text{204}\text{.23 g}}=\text{9}\text{.79}\times \text{10}^{\text{-6}}\text{mol TRP} \\ \end{align}\) Their ratio is \(\frac{n_{\text{Nin}}\text{(initial)}}{n_{\text{TRP}}\text{(initial)}}=\frac{\text{1}\text{.123}\times \text{10}^{\text{-5}}\text{mol Nin}}{\text{9}\text{.79}\times \text{10}^{\text{-6}}\text{mol TRP}}=\frac{\text{1}\text{.15 mol Nin}}{\text{1 mol TRP}}\) Since this ratio is smaller than the 2:1 stoichiometric ratio, you have insufficient Nin to react with all the TRP, so Nin is the limiting reagent. To ensure detection, in would be better to add excess Ninhydrin.
b) The amount of water product formed in a reaction may be calculated via an appropriate stoichiometric ratio from the amount of a reactant which was consumed. Some of the excess reactant TRP will be left over, but all the initial amount of Nin will be consumed. Therefore we use nNin (initial) to calculate how much H2O can be obtained
\(n_{\text{Nin}}\text{ }\xrightarrow{S\text{(water/Nin}\text{)}}\text{ }n_{\text{water}}\xrightarrow{M_{\text{water}}}\text{ }m_{\text{water}}\) \(m_{\text{water}}=\text{1}\text{.12 }\times \text{ 10}^{\text{-5}}\text{ mol Nin }\text{ }\times \text{ }\) \(\frac{\text{3 mol water}}{\text{2 mol Nin}}\text{ }\times \text{ }\frac{\text{18}\text{.016 g}}{\text{mol water}}=\text{3}\text{.02 }\times \text{ 10}^{\text{-4}}\text{ g water}\)
This is 0.302 mg water.
These calculations can be organized as a table, with entries below the respective reactants and products in the chemical equation. Calculations are shown for each possible case, assuming that one reactant is completely consumed and determining if enough of the other reactants is present to consume it. If not, that scenario is discarded.
| 2 C9H6O4 | + C11H12N2O2 → | (C9H5O2)-N=(C9H4O2)) | + C10H9NO | + CO2 | + 3 H2O | |
|---|---|---|---|---|---|---|
| m (g) | 0.0020 | 0.0020 | ||||
| M (g/mol) | 178.1 | 204.23 | 303.3 | 159.2 | 44.0 | 18.0 |
| n (mol) | 1.12 x 10-5 | 9.79 x 10-6 | -- | -- | -- | -- |
| if all C9H6O4 reacts | -1.12 x 10-5 | -5.62 x 10-6 | ||||
| Actual Reaction Amounts |
-1.12 x 10-5 | -5.62 x 10-6 | 5.62 x 10-6 | 5.62 x 10-6 | 5.62 x 10-6 | 1.68 x 10-5 |
| Actual Reaction Masses |
-0.0020 | -0.00115 | 1.71 x 10-3 | 8.93 x 10-4 | 2.47 x 10-4 | 3.02 x 10-4 |
As you can see from the example, in a case where there is a limiting reagent, the initial amount of the limiting reagent must be used to calculate the amount of product formed. Using the initial amount of a reagent present in excess would be incorrect, because such a reagent is not entirely consumed.
The concept of a limiting reagent was used by the nineteenth century German chemist Justus von Liebig (1807 to 1873) to derive an important biological and ecological law. Liebig’s law of the minimum states that the essential substance available in the smallest amount relative to some critical minimum will control growth and reproduction of any species of plant or animal life. When a group of organisms runs out of that essential limiting reagent, the chemical reactions needed for growth and reproduction must stop. Vitamins, protein, and other nutrients are essential for growth of the human body and of human populations. Similarly, the growth of algae in natural bodies of water such as Lake Erie can be inhibited by reducing the supply of nutrients such as phosphorus in the form of phosphates. It is for this reason that many states have regulated or banned the use of phosphates in detergents and are constructing treatment plants which can remove phosphates from municipal sewage before they enter lakes or streams.
References
- Vitz, E. J. Chem. Educ., 2005, 82 (7), p 1013
- Nick Saum, www.nicksaumphotography.com
- Tehuacan. emuseum.mnsu.edu/archaeolog y/sites/meso_america/tehuacan_valley.html
- The Prehistory of the Tehuacan Valley, Environment and Subsistence; Byers, D. S., Ed.; University of Texas Press: Austin, 1967.
- Kaplan, L. In The Prehistory of the Tehuacan Valley, Environment and Subsistence; Byers, D. S., Ed.; University of Texas Press: Austin, 1967; pp 202–203.
- en.Wikipedia.org/wiki/Pita
- en.Wikipedia.org/wiki/Dal_bhat
- http://www.faqs.org/nutrition/Ca-De/Corn-or-Maize-Based-Diets.html
- AUSTIN J. LEWIS, MARY B. BARNES, DALE A. GROSBACH ANDERNEST R. PEO, JR. The Journal of Nutrition, 112: 782-788, 1982; http://jn.nutrition.org/cgi/reprint/112/4/782.pdf
- http://jn.nutrition.org/cgi/reprint/112/4/782.pdf
- Nutrient Requirements of the Laboratory Rat. In: Nutrient Requirements of Laboratory Animals, 3rd. Ed.; pp. 7-37, Natiional Academy of Sciences, Washington, DC.
- www.nal.usda.gov/fnic/foodcom...st_nut_edit.pl
- en.Wikipedia.org/wiki/Amino_acid
- Schwartz, J. Radar, Hula Hoops and Playful Pigs; ECW Press: Toronto, 1999; p 31.
- en.Wikipedia.org/wiki/Ninhydrin




