3.2.2: Environment- Atom Efficiency and the 2006 Presidential Green Chemistry Award
- Page ID
- 50049
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Presidential Green Chemistry Challenge Awards [1] began in 1995 as an effort to recognize individuals and businesses for innovations in green chemistry.

IWC replica Réplica de reloj Typically five awards are given each year, one in each of five categories: Academic, Small Business, Greener Synthetic Pathways, Greener Reaction Conditions, and Designing Greener Chemicals. A committee of the American Chemical Society selects the awardees. Through 2006, a total of 57 technologies have been recognized for the award, and over 1000 nominations have been submitted.
Propylene glycol is a potential replacement for toxic ethylene glycol in antifreeze used in cars, solar heating systems, and deicing airplane wings. It is also used as a solvent in pharmaceuticals, or as a moisturizer in cosmetics, as well as the main ingredient in deodorant sticks, in fog machines, and a multitude of other uses.

It's an important enough industrial chemical that the 2006 Presidential Green Chemistry Award was given to Professor Galen J. Suppes of the University of Missouri/Columbia for an improved synthesis.
Propylene glycol is synthesized in the laboratory by oxidation of propylene (CH2CHCH3, see Figure above) with potassium permanganate:
\[3 \ce{CH_2CHCH_3} + 2 \ce{KMnO_4} + 4 \ce{H_2O} \rightarrow 3 \ce{HO-CH_2-CHOH-CH_3} + 2 \ce{MnO_2} + 2 \ce{KOH} \label{1} \]
This is considered a "good" synthesis, because it converts nearly all of the starting material to the desired product. But environmentally (and economically) it is extremely undesirable, for several reasons. It uses a non-renewable petrochemical as a reactant, uses an expensive oxidizing agent (KMnO4), produces a strong caustic (KOH) as a product and an undesirable byproduct (MnO2). It does have one advantage: It proceeds at low temperatures.
Stoichiometry
Let's abbreviate Equation \(\ref{1}\) by symbolizing propylene as P and propylene glycol as PG to make the discussion easier:
\[\ce{3 P + 2 KMnO_4 + 4 H_2O \rightarrow 3 PG + 2 MnO_2 + 2 KOH} \label{1a} \]
A balanced chemical equation such as Equation (1) above not only tells how many molecules of each kind are involved in a reaction, it also indicates the amount of each substance that is involved. Equation (1) says that 3 propylene (P) molecules react with 2 KMnO4 formula units and 4 H2O molecules to give 3 propylene glycol (PG) molecules, 2 MnO2 formula units and 2 KOH formula units. Here we use the term "formula unit" in cases where the substances are not necessarily molecules, but ionic or other species.
The equation also says that 3 mol of P reacts with 2 mol of KMnO4 and 4 mol of water yielding 2 mol of PG, 2 mol MnO2 and 2 mol of KOH.
The balanced equation does more than this, though. It also tells us that 2 × 3 = = 6 mol P will react with 2 x 2 = 4 mol KMnO4 and 2 x 4 = 8 mol water, and that ½ × 3 = 1.5 mol P requires only ½ × 2 =1 mol KMnO4 and ½ × 4 = 2 mol of H2O. In other words, the equation indicates that exactly 4 mol H2O must react for every 3 mol of P and 2 mol of KMnO4 consumed. For the purpose of calculating how much KMnO4 is required to react with a certain amount of P therefore, the significant information contained in Equation \(\ref{1}\) is the ratio
\[\dfrac{\text{2 mol KMnO}_{\text{4}}}{\text {3 mol P}} \nonumber \]
We shall call such a ratio derived from a balanced chemical equation a stoichiometric ratio and give it the symbol S. Thus, for Equation \(\ref{1}\),
\[\text{S}\left( \frac{\text{KMnO}_{\text{4}}}{\text{P}} \right)=\frac{\text{2 mol KMnO}_{\text{4}}}{\text{3 mol P}} \label{2} \]
The word stoichiometric comes from the Greek words stoicheion, “element,“ and metron, “measure.“ Hence the stoichiometric ratio measures one element (or compound) against another.
Derive all possible stoichiometric ratios from Equation \(\ref{1}\).
Solution
Any ratio of amounts of substance given by coefficients in the equation may be used:
\[\text{S}\left( \frac{\text{KMnO}_{4}}{\text{H}_{\text{2}}\text{O}} \right)=\frac{\text{2 mol KMnO}_{4}}{\text{4 mol H}_{\text{2}}\text{O}} \nonumber \]
\[\text{S}\left( \frac{\text{H}_{\text{2}}\text{O}}{\text{P}} \right)=\frac{\text{4 mol H}_{\text{2}}\text{O}}{\text{2 mol P}}\nonumber \]
\[\text{S}\left( \frac{\text{KMnO}_{4}}{\text{P}} \right)=\frac{\text{2 mol KMnO}_{4}}{\text{3 mol P}}\nonumber \]
\[\text{S}\left( \frac{\text{H}_{\text{2}}\text{O}}{\text{MnO}_{\text{2}}} \right)=\frac{\text{4 mol H}_{\text{2}}\text{O}}{\text{2 mol MnO}_{\text{2}}}\nonumber \]
\[\text{S}\left( \frac{\text{KMnO}_{4}}{\text{MnO}_{\text{2}}} \right)=\frac{\text{2 mol KMnO}_{4}}{\text{2 mol MnO}_{\text{2}}}\nonumber \]
\[\text{S}\left( \frac{\text{P}}{\text{H}_{\text{2}}\text{O}} \right)=\frac{\text{3 mol P}}{\text{4 mol H}_{\text{2}}\text{O}}\nonumber \]
There are several more stoichiometric ratios, because they can link any reactant to any other reactant, any reactant to any product, or any product to any other product. When any chemical reaction occurs, the amounts of substances consumed or produced are related by the appropriate stoichiometric ratios. Using Equation \ref{1} as an example, this means that the ratio of the amount of KMnO4 consumed to the amount of propylene (P) consumed must be the stoichiometric ratio S(KMnO4/P):
\[\frac{n_{\text{KMnO}_{\text{4}}\text{ consumed}}}{n_{\text{P consumed}}} = \text{S}\left( \frac{\text{KMnO}_{\text{4}}}{\text{P}} \right)=\frac{\text{2 mol KMnO}_{\text{4}}}{\text{3 mol P}} \nonumber \]
Similarly, the ratio of the amount of MnO2 produced to the amount of P consumed must be S(MnO2/P):
\[\frac{n_{\text{MnO}_{\text{2}}\text{ produced}}}{n_{\text{P consumed}}} = \text{S}\left( \frac{\text{MnO}_{\text{2}}}{\text{P}} \right) = \frac{\text{2 mol MnO}_{\text{2}}}{\text{3 mol P}} \nonumber \]
In general we can say that
\(\text{Stoichiometric ratio }\left( \frac{\text{X}}{\text{Y}} \right)=\frac{\text{amount of X consumed or produced}}{\text{amount of Y consumed or produced}}\text{ (3}\text{a)} \nonumber \]
or, in symbols,
\[\text{S}\left( \frac{\text{X}}{\text{Y}} \right)=\frac{n_{\text{X consumed or produced}}}{n_{\text{Y consumed or produced}}}\text{ (3}\text{b)} \nonumber \]
Note that in the word Equation \ref{3a} and the symbolic Equation \ref{3b}, X and Y may represent any reactant or any product in the balanced chemical equation from which the stoichiometric ratio was derived. No matter how much of each reactant we have, the amounts of reactants consumed and the amounts of products produced will be in appropriate stoichiometric ratios.
If 3.68 mol propylene (P) is consumed according to Equation \ref{1}, find the amounts of (a) potassium permanganate (KMnO4) required, and the amounts of
- propylene glycol, PG, and
- MnO2 produced (assuming plenty of the other reactant, water is available).
Solution
a. The amount of KMnO4 required must be in the stoichiometric ratio S(KMnO4 / P) to the amount of propylene consumed:
\[\text{S}\left( \frac{\text{KMnO}_{4}}{\text{P}} \right) = \frac{n_{\text{KMnO}_{\text{4 consumed}}}}{n_{\text{P consumed}}} \nonumber \]
Multiplying both sides nP consumed, by we have \(n_{\text{KMnO}_{\text{4 consumed}}} = n_{\text{P consumed}}\times \text{S}\left( \frac{\text{KMnO}_{4}}{\text{P}} \right) = \text{3}\text{.68 mol P}\times \frac{\text{2 mol KMnO}_{4}}{\text{3 mol P}}=\text{2}\text{.45 mol KMnO}_{4}\)
b. The amount of propylene glycol produced must be in the stoichiometric ratio S(PG/P) to the amount of propylene consumed:
\[\text{S}\left( \frac{\text{PG}}{\text{P}} \right)=\frac{n_{\text{PG produced}}}{n_{\text{P consumed}}} \nonumber \]
Multiplying both sides nP consumed, by we have
\[n_{\text{PG produced}}=n_{\text{P consumed}}\times \text{S}\left( \frac{\text{PG}}{\text{P}} \right) = \text{3}\text{.68 mol P}\times \frac{\text{3 mol PG}}{\text{3 mol P}}=\text{3}\text{.68 mol PG} \nonumber \]
c. Similarly, the amount of MnO2 produced must be in the stoichiometric ratio S(MnO2 / P) to the amount of propylene consumed:
\[\text{S}\left( \frac{\text{MnO}_{2}}{\text{P}} \right) = \frac{n_{\text{MnO}_{\text{2 produced}}}}{n_{\text{P consumed}}} \nonumber \]
Multiplying both sides nP consumed, by we have
\[n_{\text{MnO}_{\text{2 produced}}} = n_{\text{P consumed}}\times \text{S}\left( \frac{\text{MnO}_{2}}{\text{P}} \right) = \text{3}\text{.68 mol P}\times \frac{\text{2 mol MnO}_{2}}{\text{3 mol P}}=\text{2}\text{.45 mol MnO}_{2} \nonumber \]
These calculations can be organized as a table, with entries below the respective reactants and products in the chemical equation. You may verify the additional calculations.
| 3 CH2CHCH3 | + 2 KMnO4 | + 4 H2O → | 3 CH2(OH)CH(OH)CH3 | + 2 MnO2 | + 2 KOH | |
|---|---|---|---|---|---|---|
| n (mol) | 3.68 | 2.45 | 4.91 | 3.68 | 2.45 | 2.45 |
This is a typical illustration of the use of a stoichiometric ratio as a conversion factor. Example 2 is analogous to Examples 1 and 2 from Conversion Factors and Functions, where density was employed as a conversion factor between mass and volume. Example 2 is also analogous to Examples 2.4 and 2.6, in which the Avogadro constant and molar mass were used as conversion factors. As in these previous cases, there is no need to memorize or do algebraic manipulations with Equation \ref{3} when using the stoichiometric ratio. Simply remember that the coefficients in a balanced chemical equation give stoichiometric ratios, and that the proper choice results in cancellation of units. In road-map form
\[\text{amount of X consumed or produced}\overset{\begin{smallmatrix} \text{stoichiometric} \\ \text{ ratio X/Y} \end{smallmatrix}}{\longleftrightarrow}\text{amount of Y consumed or produced} \nonumber \]
or symbolically.
\[n_{\text{X consumed or produced}}\text{ }\overset{S\text{(X/Y)}}{\longleftrightarrow}\text{ }n_{\text{Y consumed or produced}} \nonumber \]
When using stoichiometric ratios, be sure you always indicate moles of what. You can only cancel moles of the same substance. In other words, 1 mol KMnO4 cancels 1 mol KMnO4 but does not cancel 1 mol H2O.
Masses of Reactants and Products
We can also calculate the masses of reactants and products. The molar masses can be determined from the formulas, and the masses are calculated as follows:
m (g)= n (mol) x M (g/mol)
For KMnO4,
mKMnO4 = nKMnO4 x MKMnO4
mKMnO4 = 2.45 mol x 158.03 g/mol = 387.17 g
This result is added to the table below, and you may want to see if you can verify the other results in the table.
| 3 CH2CHCH3 | + 2 KMnO4 | + 4 H2O → | 3 CH2(OH)CH(OH)CH3 | + 2 MnO2 | + 2 KOH | |
|---|---|---|---|---|---|---|
| n (mol) | 3.68 | 2.45 | 4.91 | 3.68 | 2.45 | 2.45 |
| M (g/mol) | 42.08 | 158.03 | 18.02 | 76.10 | 86.94 | 56.11 |
| m(g) | 155 | 387 | 88.47 | 280 | 213 | 138 |
Atom Economy
Notice that there seems to be an aweful lot of extraneous stuff in this synthesis. It requires 387 g of KMnO4, but that results only in the addition of two -OH groups to each propylene molecule (and they may come,in part, from H2O).
As a measure of this inefficiency, Barry trost developed the concept of atom economy, and for this work he received the Presidential Green Chemistry Challenge Award in 1998[2]. The percentage atom economy is defined as
\[\text{% atom economy} = \dfrac{\text{mass of atoms utilized}}{\text{mass of all reactant atoms}} \times 100\% \label{atomecon}\]
So we see that the mass of reactants that actually end up in products is 155 g (3.68 mol) of propylene and 125.2 g of OH groups (2 x 3.68 mol, or 7.36 mol, with a molar mass of 17.01 g/mol OH), for a total of 280 g. The mass of all reactants is
155 g + 387 g + 88.5 g = 630 g,
so the percent atom efficiency is (via Equation \ref{atomecon})
\[\text{% atom economy} = \dfrac{280 g}{630 g} x 100% = 44.4% \nonumber\]
We see that a lot of atoms are wasted in this synthesis. For comparison, let's look at several industrial processes that have been developed.
Professor Suppes’s system that won the Green Chemistry Award couples a new copper-chromite catalyst to convert glycerin to propylene glycol. First, it utilizes a byproduct of biodiesel synthesis, glycerine (rather than the propylene used above, which comes from petroleum). Second, it uses a catalyst, which is not consumed in a chemical reaction and thus does not reduce the atom economy. Finally, this process uses a lower temperature and lower pressure than do previous systems (428 °F versus 500 °F and <145 psi versus >2,170 psi), and produces less byproduct than do similar catalysts[3].
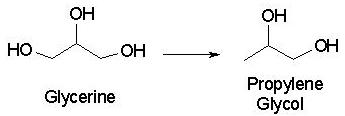
The synthesis of propylene glycol from glycerine
The reaction involves dehydration (removal of -H and -OH, or H2O) of glycerine, (yielding 2,3-dihydroxypropene or 3-hydroxypropanal) followed by hydrogenation of the resulting double bond to give the final product. The overall equation for the reaction is
\[\ce{H2 + HO-CH2CH(OH)CH2OH → HO-CH2-CHOH-CH3 + H2O } \label{4} \]
Calculate the mass of hydrogen that's required to react with 100 g of glycerine, and the masses of propylene glycol and water that result in the Suppes Green Synthesis of propylene glycol.
Solution
First, we'll start the same kind of table that we used above, but we'll start with the information we have: the mass of glycerine, and the molar masses that we can calculate from formulas:
| HO-CH2CH(OH)CH2OH | + H2 → | CH2(OH)CH(OH)CH3 | + H2O | |
|---|---|---|---|---|
| M (g/mol) | 92.1 | 2.02 | 76.10 | 18.02 |
| m (g) | 100 | |||
| n(mol) |
We know that the stoichiometry of the reaction involves the amounts of reactants and products, not their masses, so we'll convert each mass to an amount. For example, the amount of glycerine is:
\[\begin{align*} n(mol) &= \dfrac{m(g)}{M\, (g/mol)} \\[4pt] &= \dfrac{100\, g}{92.1\, g/mol} \\[4pt] &= 1.09\, mol \end{align*} \]
| HO-CH2CH(OH)CH2OH | + H2 → | CH2(OH)CH(OH)CH3 | + H2O | |
|---|---|---|---|---|
| M (g/mol) | 92.1 | 2.02 | 76.10 | 18.02 |
| m (g) | 100 | |||
| n(mol) | 1.09 |
We can easily calculate the other amounts, because the stoichiometric ratios are all 1. So for the amount of hydrogen consumed:
\[\text{n}_{\text{H}_{2}} = \text{n}_{\text{HO-CH}_{2}\text{CH(OH)CH}_{2}\text{OH}} ~x~\frac{\text{1 mol H}_{2}}{\text{1 mol HO-CH}_{2}\text{CH(OH)CH}_{2}\text{OH}} \nonumber \]
\[\text{n}_{\text{H}_{2}} = \text{1.09 mol} ~x~\frac{\text{1 mol H}_{2}}{\text{1 mol HO-CH}_{2}\text{CH(OH)CH}_{2}\text{OH}} = 1.09 mol \nonumber \]
| HO-CH2CH(OH)CH2OH | + H2 → | CH2(OH)CH(OH)CH3 | + H2O | |
|---|---|---|---|---|
| M (g/mol) | 92.1 | 2.02 | 76.10 | 18.02 |
| m (g) | 100 | |||
| n(mol) | 1.09 | 1.09 | 1.09 | 1.09 |
Now we can use the amounts to calculate the masses of the other reactants and products, remembering that
m(g) = n(mol) x M(g/mol).
So for hydrogen,
mH2 = 1.09 mol x 2.02 g/mol = 2.20 g.
Verify the other table entries:
| HO-CH2CH(OH)CH2OH | + H2 → | CH2(OH)CH(OH)CH3 | + H2O | |
|---|---|---|---|---|
| M (g/mol) | 92.1 | 2.02 | 76.10 | 18.02 |
| m (g) | 100 | 2.20 | 83.0 | 19.6 |
| n(mol) | 1.09 | 1.09 | 1.09 | 1.09 |
Now we can calculate the percent atom economy for this process:
% atom economy = \(\frac{mass ~of ~atoms ~utilized}{mass ~of~all ~reactant ~atoms} x 100%\)
All of the atoms in the reactants except one oxygen atom which is removed from the glycerine. Since we have 1.09 mol of glycerine, the mass of oxygen not incorporated into product is 1.09 mol O x 15.999 g/mol O = 17.44 g O. The mass of reactants utilized is therefore 100 g - 17.44 g = 82.56 g, and the mass of product formed is 83.0 g.
percent atom economy = \(\frac{82.56}{83.0} ~x~ 100% = 99.5%\)
Not only that, but the product, water, is innocuous, and it uses an overproduced reactant! The main cost is heating and pressurizing the reactor.
What mass of oxygen would be consumed when 3.3 × 1015 g, 3.3 Pg (petagrams), of octane (C8H18) is burned to produce CO2 and H2O?
Solution
First, write a balanced equation
\[\ce{2C8H18 + 25O2 → 16CO2 + 18H2O} \nonumber \]
The problem gives the mass of C8H18 burned and asks for the mass of O2 required to combine with it. Thinking the problem through before trying to solve it, we realize that the molar mass of octane could be used to calculate the amount of octane consumed. Then we need a stoichiometric ratio to get the amount of O2 consumed. Finally, the molar mass of O2 permits calculation of the mass of O2. Symbolically
\[m_{\text{C}_{\text{8}}\text{H}_{\text{18}}}\text{ }\xrightarrow{M_{\text{C}_{\text{8}}\text{H}_{\text{18}}}}\text{ }n_{\text{C}_{\text{8}}\text{H}_{\text{18}}}\text{ }\xrightarrow{S\text{(SO}_{\text{2}}\text{/C}_{\text{8}}\text{H}_{\text{18}}\text{)}}\text{ }n_{\text{O}_{\text{2}}}\xrightarrow{M_{\text{O}_{\text{2}}}}\text{ }m_{\text{O}_{\text{2}}} \nonumber \]
\[m_{\text{O}_{\text{2}}}=\text{3}\text{.3 }\times \text{ 10}^{\text{15}}\text{ g }\times \text{ }\frac{\text{1 mol C}_{\text{8}}\text{H}_{\text{18}}}{\text{114 g}}\text{ }\times \text{ }\frac{\text{25 mol O}_{\text{2}}}{\text{2 mol C}_{\text{8}}\text{H}_{\text{18}}}\text{ }\times \text{ }\frac{\text{32}\text{.00 g}}{\text{1 mol O}_{\text{2}}}=\text{1}\text{.2 }\times \text{ 10}^{\text{16}}\text{ g } \nonumber \]
Thus 12 Pg (petagrams) of O2 would be needed. The large mass of oxygen obtained in this example is an estimate of how much O2 is removed from the earth’s atmosphere each year by human activities. Octane, a component of gasoline, was chosen to represent coal, gas, and other fossil fuels. Fortunately, the total mass of oxygen in the air (1.2 × 1021 g) is much larger than the yearly consumption. If we were to go on burning fuel at the present rate, it would take about 100 000 years to use up all the O2. Actually we will consume the fossil fuels long before that! One of the least of our environmental worries is running out of atmospheric oxygen.
References
- www.epa.gov/greenchemistry/pu...c/presgcc.html
- en.Wikipedia.org/wiki/Green_chemistry
- Lekha Charan Meher†, Rajesh Gopinath, S. N. Naik and Ajay K. Dalai. Ind. Eng. Chem. Res., 2009, 48 (4), pp 1840–1846


