3.2.1: Cultural Connections- Berthollides- A Challenge to Chemical Stoichiometry
- Page ID
- 50046
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Stoichiometry
Chemists are committed to the idea that a balanced chemical equation such as:
\[2 Fe + O_2 \rightarrow 2 FeO \label{1} \]
not only tells how many atoms or molecules of each kind are involved in a reaction, it also indicates the amount of each substance that is involved. Equation (1) says that 1 Fe atom can react with 2 O2 molecules to give 2 formula units of FeO. Here we're using the term "formula unit" to indicate that the substance may not be a molecule, but rather an ionic compound or ["network crystal"]. A "formula unit" gives the composition of the substance without specifying the type of bonding.
The equation also says that 1 mol of Fe atoms would react with 2 mol O2 yielding 2 mol FeO.
We have become so accustomed to the idea of atoms, that it seems logical that equations should represent whole numbers of atoms. We now talk about the stoichiometric ratios of atoms when we want to indicate that they must combine in small whole number ratios, like 1:1 in FeO. The word stoichiometric comes from the Greek words stoicheion, “element,“ and metron, “measure.“ Hence the stoichiometric ratio measures one element (or compound) against another.
A Challenge to Stoichiometric Reasoning
But the idea of whole number stoichiometric ratios was strongly opposed in the early nineteenth century. This is understandable, because the Law of Definite Proportions is quite anti-intuitive. After all, it seems that you can generally mix things in virtually any ratio to get desired results. Since Dalton's atomic theory implied that atoms should combine in definite ratios, many of his contemporaries opposed the atomic theory. Dalton's theory explained Proust's earlier Law of constant composition (Law of Definite Proportions or "Proust's Law"(1797)) [1],
There are in fact many important compounds that are "non-stoichiometric", including the product of Equation (1)! They are often called "Berthollides" after French inorganic chemist Claude Louis Berthollet (1748–1822), who attacked Dalton's atomic theory (1803-5) and Proust's Law [2]. N. S. Kurnakov introduced the terms "Daltonides" and "Berthollides" in 1912–14 to designate chemical compounds of constant composition (Daltonides) and variable composition (Berthollides)[3].
|
Claude Louis Berhollet. Opponent of the Law of Constant Composition |
Joseph Proust (1754-1826). Discoverer of Law of Constant Composition |
This episode in the history of chemistry is a good example of the claim by philosophers of science that counterexamples to an accepted theory may not be recognized. The concept of stoichiometry was used to cover up the most glaring exceptions, and, for more than a century, substances that could not be made to fit these new rules were ignored until Kurnakov called attention to Berthollides[4][5].
Non-stoichiometric Compounds
Berthollet opposed Dalton's atomic theory, pointing to many reactions, like the reaction of many transition metals with oxygen, that are not stoichiometric. Some of his writings are available online. The reaction in Equation (1) often does not give FeO. In nature, FeO is the mineral wüstite, which has the actual stoichiometry closer to Fe0.95O. For each "missing" Fe2+ ion, the crystal contains two Fe3+ ions to supply the missing 2+ charge for charge balance[6]. In the diagram below, one vacancy (Fe2+) compensated by two substitutions (Fe3+) at lateice points. The "Frenkel Pair" occurs when a lattice ion is replaced by an interstitial ion in some nonstoichiometric compounds. The composition of a non-stoichiometric compound may vary only slightly, as in wüstite where the formula may be written as Fe1-xO, where x is a small number (~0.05). In some cases, like copper sulphides, the variation can be much larger[7]. For practical purposes, the term describes materials where the non-stoichiometry is at least 1% of the ideal composition.
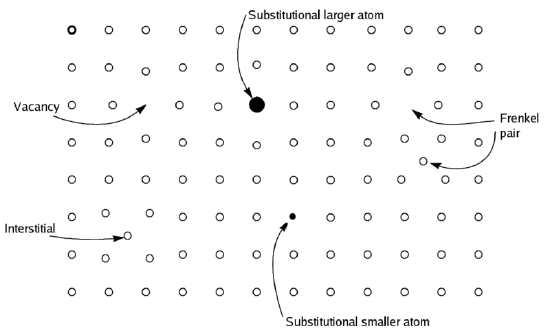
Details of Stoichiometric Reasoning
To contrast stoichiometric with nonstoichiometric compounds, refer to Equation (2),
\[3 Fe + 2 O_2 \rightarrow Fe_3O_4 \label{2} \]
In addition to atom ratios, it also tells us that 2 × 3 mol = 6 mol Fe will react with 2 × 2 mol = 4 mol O2, and that ½ × 3 mol = 1.5 mol Fe requires only ½ × 2 mol = 1 mol O2. In other words, the equation indicates that exactly 2 mol O2 must react for every 3 mol Fe consumed. For the purpose of calculating how much O2 is required to react with a certain amount of Fe therefore, the significant information contained in Eq. (2) is the ratio
\[\dfrac{\text{2 mol O}_{\text{2}}}{\text{3 mol Fe}} \nonumber \]
We shall call such a ratio derived from a balanced chemical equation a stoichiometric ratio and give it the symbol S. Thus, for Eq. (2),
\[\text{S}\left( \frac{\text{O}_{\text{2}}}{\text{Fe}} \right)=\frac{\text{2 mol O}_{\text{2}}}{\text{3 mol Fe}} \tag{3}\]
Stoichiometric Reasoning and Non-Stoichiometric Compounds
Under normal circumstances, the stoichiometric ratio holds closely (Fe3O4 is a combination of Fe2O3 and FeO, so it may incorporate the nonstoichiometry of FeO described above). But unusual geological or synthetic conditions lead to other stoichiometries. For example, a technique called "sputter deposition" or "Sputtering" involves heating one reactant in a vacuum with a small amount of the second reactant present as a vapor, as shown in the Figure at right. The product is collected on a cold substrate.
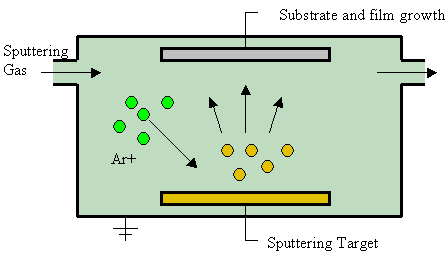
This leads to berthollides when an iron sample is sputtered in the presence of water vapor. Oxide compositions ranging from Fe3O4 to Fe2O3, were obtained, depending on the temperature and pressure [8]. They would have stoichiometric ratios ranging from \(\frac{\text{2 mol O}_{\text{2}}}{\text{3 mol Fe}}\) for Equation (2).
to \(\frac{\text{1.5 mol O}_{\text{2}}}{\text{2 mol Fe}}\) for the reaction 2 Fe + 1.5 O2 → Fe2O3, and most of the ratios would not be easily reduced to whole number ratios.
It is remarkable that stoichiometric ratios are used to understand and guide the synthesis of even non-stoichiometric compounds, so this is truly an important area of chemistry.
Derive all possible stoichiometric ratios from Eq. (2)
Solution
Any ratio of amounts of substance given by coefficients in the equation may be used:
\[\text{S}\left( \frac{\text{Fe}}{\text{O}_{2}} \right)=\frac{\text{3 mol Fe}}{\text{2 mol O}_{\text{2}}}~~~~~~\text{S}\left( \frac{\text{Fe}_{3}\text{O}_{4}}{\text{Fe}} \right)=\frac{\text{1 mol Fe}_{3}\text{O}_{4}}{\text{3 mol Fe}}\] \[\text{S}\left( \frac{\text{O}_{2}}{\text{Fe}_{3}\text{O}_{4}} \right)=\frac{\text{2 mol O}_{2}}{\text{1 mol Fe}_{2}\text{O}_{4}}~~~~~\text{S}\left( \frac{\text{Fe}}{\text{Fe}_{\text{3}}\text{O}_{4}} \right)=\frac{\text{3 mol Fe}}{\text{1 mol Fe}_{\text{3}}\text{O}_{4}}\]
When any stoichiometric chemical reaction occurs, the amounts of substances consumed or produced are related by the appropriate stoichiometric ratios. Using Eq. (2) as an example, this means that the ratio of the amount of O2 consumed to the amount of Fe consumed must be the stoichiometric ratio S(O2/Fe): \(\frac{n_{\text{O}_{\text{2}}\text{ consumed}}}{n_{\text{Fe}_\text{ consumed}}}=\text{S}\left( \frac{\text{O}_{\text{2}}}{\text{Fe}} \right)=\frac{\text{2 mol O}_{\text{2}}}{\text{3 mol Fe}}\) Similarly, the ratio of the amount of Fe3O4 produced to the amount of Fe consumed must be
S(Fe3O4/Fe):
\[\frac{n_{\text{Fe}_{3}\text{O}_{4}}\text{ produced}}{n_{\text{Fe}\text{ consumed}}}\]
Note that in the word Eq. (4a) and the symbolic Eq. (4b), X and Y may represent any reactant or any product in the balanced chemical equation from which the stoichiometric ratio was derived. No matter how much of each reactant we have, the amounts of reactants consumed and the amounts of products produced will be in appropriate stoichiometric ratios.
Find the amount of Fe3O4 produced when 3.68 mol Fe is consumed according to Eq. (2).
Solution
The amount of Fe3O4 produced must be in the stoichiometric ratio S(Fe3O4/Fe) to the amount of Fe consumed:
\[\text{S}\left( \frac{\text{Fe}_{3}\text{O}_{4}}{\text{Fe}} \right)\]
Multiplying both sides nFe consumed, by we have
\[n_{\text{Fe}_{3}\text{O}_{4}\text{ produced}}\]
This is a typical illustration of the use of a stoichiometric ratio as a conversion factor. Example 2 is analogous to Examples 1 and 2 from Conversion Factors and Functions, where density was employed as a conversion factor between mass and volume. Example 2 is also analogous to Examples 2.4 and 2.6, in which the Avogadro constant and molar mass were used as conversion factors. As in these previous cases, there is no need to memorize or do algebraic manipulations with Eq. (4) when using the stoichiometric ratio. Simply remember that the coefficients in a balanced chemical equation give stoichiometric ratios, and that the proper choice results in cancellation of units. In road-map form \(\text{amount of X consumed or produced}\overset{\begin{smallmatrix} \text{stoichiometric} \\ \text{ ratio X/Y} \end{smallmatrix}}{\longleftrightarrow}\text{amount of Y consumed or produced}\) or symbolically.
-
-
- \(n_{\text{X consumed or produced}}\text{ }\overset{S\text{(X/Y)}}{\longleftrightarrow}\text{ }n_{\text{Y consumed or produced}}\)
-
When using stoichiometric ratios, be sure you always indicate moles of what. You can only cancel moles of the same substance. In other words, 1 mol Fe cancels 1 mol Fe but does not cancel 1 mol Fe3O4.
The next example shows that stoichiometric ratios are also useful in problems involving the mass of a reactant or product.
Add example text here.
Solution
Add example text here.
Calculate the mass of Oxygen (O2) consumed when 3.68 mol Fe reacts according to Equation (2).
Solution
The problem asks that we calculate the mass of O2 consumed. As we learned in Example 2 of The Molar Mass, the molar mass can be used to convert from the amount of O2 to the mass of O2. Therefore this problem in effect is asking that we calculate the amount of O2 consumed from the amount of Fe consumed. This is the same problem as in Example 2. It requires the stoichiometric ratio
\[\text{S}\left( \frac{\text{O}_{\text{2}}}{\text{Fe}} \right)=\frac{\text{2 mol O}_{\text{2}}}{\text{3 mol Fe}}\] \[n_{\text{O}_{\text{2}}}\text{ consumed}\]
The mass of O2 is \(\text{m}_{\text{O}_{\text{2}}}=\text{2}\text{.45 mol O}_{\text{2}}\times \frac{\text{32}\text{.0 g O}_{\text{2}}}{\text{1 mol O}_{\text{2}}}=\text{78.5 g O}_{\text{2}}\) With practice this kind of problem can be solved in one step by concentrating on the units. The appropriate stoichiometric ratio will convert moles of Fe to moles of O2 and the molar mass will convert moles of O2 to grams of O2. A schematic road map for the one-step calculation can be written as \(n_{\text{Fe}}~~\xrightarrow{S\text{(O}_{\text{2}}\text{/Fe}\text{)}}~~n_{\text{O}_{\text{2}}}~~\xrightarrow{M_{\text{O}_{\text{2}}}}\text{ }m_{\text{O}_{\text{2}}}\) Thus \(\text{m}_{\text{O}_{\text{2}}}=\text{3.68 mol Fe}~~\times ~~\frac{\text{2 mol O}_{\text{2}}}{\text{3 mol Fe}}~~\times~~\frac{\text{32.0 g}}{\text{1 mol O}_{\text{2}}}=\text{78.5 g O}_{2}\)
These calculations can be organized as a table, with entries below the respective reactants and products in the chemical equation. You may verify the additional calculations of the mass of product.
| 3 Fe | + 2 O2 → | 1 Fe3O4 | |
|---|---|---|---|
| m (g) | 205.5 | 78.5 | 284.0 |
| M (g/mol) | 55.845 | 32.0 | 231.54 |
| n (mol) | 3.68 | 2.45 | 1.23 |
Example 4
We noted above that when iron is sputtered in the presence of water vapor, a range of products from Fe3O4 to Fe2O3 (common rust) may be produced. Prepare a table similar to the one above for the reaction in which 0.200 g of Fe is converted to Fe2O3.
Solution
First, write a balanced equation
2 Fe + 3 H2O → Fe2O3 + 3 H2 The problem gives the mass of Fe. Thinking the problem through before trying to solve it, we realize that the molar mass of Fe could be used to calculate the amount of Fe consumed. Then we need a stoichiometric ratio to get the amount of O2 consumed and the amount of Fe2O3 and H2 produced. Finally, the molar masses of O2, Fe2O3, and H2 permit calculation of the mass of O2, Fe2O3, and H2.
We might start the table by entering the given mass, and the molar masses which we calculate from atomic weight tables:
| 2 Fe | + 3 H2O → | 2 Fe2O3 | + 3 H2 | |
|---|---|---|---|---|
| m (g) | 0.200 | |||
| M (g/mol) | 55.845 | 32.0 | 159.69 | 2.016 |
| n (mol) |
Now we can calculate the amount of Fe present:
\[\text{n (mol)}~~ = ~~\frac{\text{m (g)}}{\text{M (g/mol)}}\] \[\text{n (mol)} ~~=~~\frac{\text{0.200 g Fe}}{\text{55.847 g/mol}}~~=~~\text{0.00358 mol Fe}\]
Then the stoichiometric ratios are used to calculate the amounts of water and products:
\[\text{S}\left( \frac{\text{H}_{\text{2}}\text{O}}{\text{Fe}} \right)=\frac{\text{3 mol H}_{\text{2}}\text{O}}{\text{2 mol Fe}}\]
So the amount of water required is
0.00358 mol Fe x (3 mol H2O / 2 mol Fe) = 0.00537 mol H2O
Similarly, we use the stoichiometric ratio to calculate the amount of product:
\[\text{S}\left( \frac{\text{Fe}_{\text{2}}\text{O}_{3}}{\text{Fe}} \right)=\frac{\text{1 mol Fe}_{\text{2}}\text{O}_{3}}{\text{2 mol Fe}}\]
So the amount of Fe2O3 produced is
0.00358 mol Fe x (1 mol Fe2O3 / 2 mol Fe) = 0.00179 mol Fe2O3.
The amount of H2 produced must be the same as the amount of water consumed, since they are in the ratio 3:3 from the equation.
We can add these to the table:
| 2 Fe | + 3 H2O → | 2 Fe2O3 | + 3 H2 | |
|---|---|---|---|---|
| m (g) | 0.200 | |||
| M (g/mol) | 55.845 | 32.0 | 159.69 | 2.016 |
| n (mol) | 0.00358 | 0.00537 | 0.00179 | 0.00537 |
Finally, we can use the molar masses to convert from amounts (in mol) to masses (in g):
| 2 Fe | + 3 H2O → | 2 Fe2O3 | + 3 H2 | |
|---|---|---|---|---|
| m (g) | 0.200 | 0.097 | 0.286 | 0.0108 |
| M (g/mol) | 55.845 | 18.015 | 159.69 | 2.016 |
| n (mol) | 0.00358 | 0.00537 | 0.00179 | 0.00537 |
Note that the sum of the masses of reactants equals the sum of the masses of the products.
References
- en.Wikipedia.org/wiki/Joseph_Proust
- en.Wikipedia.org/wiki/Claude_Louis_Berthollet
- http://encyclopedia2.thefreedictionary.com/Daltonides+and+Berthollides
- J.P. Suchet, Daltonides, berthollides and inorganic glasses"; Journal of Non-Crystalline Solids, V.6, #4, (1971) 370-392
- www.sciencedirect.com/science...5&searchtype=a
- en.Wikipedia.org/wiki/Non-stoichiometric_compound
- en.Wikipedia.org/wiki/Copper_sulfide
- jap.aip.org/resource/1/japiau...sAuthorized=no




