2.12.3: Foods- Iron Supplements
- Page ID
- 50709
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Iron supplements are available as dietary supplements in food markets (where they are not controlled by the FDA) or by prescription, for treatment of TAG Heuer Replica, the most common blood disorder. Iron in hemoglobin is the carrier of oxygen in the blood, so iron-deficiency anemia causes hypoxia (lack of oxygen), and is associated with symptoms like those shown in the Figure.

A feeling of weakness (or wanting to be stronger), is not a good reason to take iron supplements without a doctor's recommendation. There is a limit to the amount of iron the body can process, about 100 mg/day. Iron is toxic if taken in overload, and can cause vomiting, diabetes, damage to the liver, heart, and endochrine glands, and may cause premature death [1][2]. Approximately 3 g is lethal for a 2 year old, so supplements must be kept inaccessible to children. Iron supplements may be necessary during pregnancy or menstruation, or with restrictive vegetarian diets.
Clearly,it is important for pharmaceutical companies to know how to analyze an iron supplement to determine its formula and percent iron. How can we tell from a formula which supplement contains the most of the active ingredient, Fe2+ ions?
Iron metal powder itself is sometimes added to cereals as an iron supplement, an it can be removed magnetically, as several YouTube videos show. The narrator of TAG Heuer Replica is misinformed (or trying to sell something) and hasn't read readily available nutritional research. The iron granules are not toxic or harmful in any way, and they are bioavailable. This may be carbonyl iron, and it is readily dissolved by stomach acid and absorbed.
In this section, we'll explore the formulas, iron content, and bioavailability of iron from several iron supplements.
Determining Percent Composition
Carbonyl Iron
The iron particles in cereal are probably made by decomposing iron carbonyl:
"Iron Carbonyl" → Fe + CO
How do we know what the formula for iron carbonyl, so we can better understand the synthesis of "carbonyl iron particles"? We can determine it as follows:
When 10.00 g of iron carbonyl is decomposed, it yields 2.85 g of iron and gaseous CO, which contains 3.06 g of carbon and the remainder oxygen. Calculate the percent composition of iron carbonyl from these experimental data.
Solution
The percentage of iron is the mass of iron divided by the total mass of compound times 100 percent:
\(\text{ }\!\!%\!\!\text{ Fe = }\frac{m_{\text{Fe}}}{m_{\text{compound}}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = }\frac{\text{2}\text{.85 g}}{\text{10}\text{.0 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 28}\text{.5 }\!\!%\!\!\text{ }\)The iron and carbon constitute 2.85 + 3.06 = 5.91 g.
The remainder of the compound (10.0 g – 5.91 g = 4.09 g) is oxygen.
\(\text{ }\!\!%\!\!\text{ O = }\frac{m_{\text{O}}}{m_{\text{compound}}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = }\frac{\text{4}\text{.09 g}}{\text{10}\text{.0 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 40}\text{.9 }\!\!%\!\!\text{ }\)Similarly, the percent C is 30.6.
As a check, verify that the percentages add to 100:
28.5 + 40.9 + 30.6 = 100%Determining Formulas from Percent Composition
To obtain the formula from percent-composition data, we must find how many carbon and oxygen atoms there are per iron atom. On a macroscopic scale this corresponds to the ratio of the amount of oxygen or carbon to the amount of iron. If the formula is FeC2O2, it not only indicates that there are two carbon atoms and two oxygen atoms per iron atom, it also says that there are 2 mol of carbon and oxygen atoms for each 1 mol of iron atoms. That is, the amount of carbon or oxygen is twice the amount of iron. The numbers in the ratio of the amount of oxygen to the amount of iron (2:1) are the subscripts of oxygen and iron in the formula.
Determine the formula for the compound whose percent composition was calculated in the previous example.
Solution
For convenience, assume that we have 100 g of the compound. Of this, 28.5 g (28.5%) is iron, 30.6 g is carbon, and 40.9 g is oxygen. Each mass can be converted to an amount of substance
\(\begin{align} & n_{\text{Fe}}=\text{28}\text{.5 g}\times \frac{\text{1 mol Fe}}{\text{55}\text{.85 g}}=\text{0}\text{.510 mol Fe} \\ & n_{\text{O}}=\text{40}\text{.9 g}\times \frac{\text{1 mol O}}{\text{15}\text{.99 g}}=\text{2}\text{.56 mol O} \\ & n_{\text{C}}=\text{30}\text{.6 g}\times \frac{\text{1 mol C}}{\text{12}\text{.0 g}}=\text{2}\text{.56 mol C} \\ \end{align}\) Dividing all by the smallest amount, we have\(\frac{n_{\text{C}}}{n_{\text{Fe}}}=\frac{\text{2}\text{.55 mol C}}{\text{0}\text{.510 mol Fe}}=\frac{\text{5}\text{.01 mol C}}{\text{1 mol Fe}}\)
\(\frac{n_{\text{O}}}{n_{\text{Fe}}}=\frac{\text{2}\text{.55 mol O}}{\text{0}\text{.510 mol Fe}}=\frac{\text{5}\text{.01 mol O}}{\text{1 mol Fe}}\)
So the formula is FeC5O5 or Fe(CO)5.
The ratio 5.01 mol C and 5.01 mol O to 1 mol Fe also implies that there are 5.01 oxygen atoms and 5.01 carbon atoms per 1 Fe atom. If the atomic theory is correct, there is no such thing as 0.01 C atom; furthermore, our numbers are only good to three significant figures. Therefore we round 2.01 to 2 and write the formula as FeC5O5. This is an interesting compound of iron and carbon monoxide. It is a liquid at room temperature, and is quite toxic.
The dietary supplement is thus prepared according to the equation:
Fe(CO)5 → Fe + 5 CO
Ferrous Sulfate
Iron Sulfate (Feratab®, MyKidz Iron 10®, etc.) is made by oxidizing pyrite ore:
- FeS2 + O2 + H2O → Ferrous Sulfate + H2SO4
But how do we know what the product is, so we know how use it, and how to balance the equation?
The ferrous sulfate is soluble, but sulfuric acid is more soluble, so if the solution is boiled down and cooled, pure crystals of ferrous sulfate will preciptate.
Once a pure product has been obtained, it may be possible to identify the substance by means of its physical and chemical properties. Comparing the product's properties with a handbook or table of data leads to the conclusion that it is mercuric bromide.
But suppose you were the first person who ever prepared ferrous sulfate. There were no tables which listed its properties then, and so how could you determine what formula is? One answer involves quantitative analysis—the determination of the percentage by mass of each element in the compound. Such data are usually reported as the percent composition.
Ferrous sulfate has the composition 36.8% Fe, 21.1% S and 42.1% O. Find its formula.
Solution Again assume a 100-g sample and calculate the amount of each element:
\(\begin{align} & n_{\text{Fe}}=\text{36}\text{.8 g}\times \frac{\text{1 mol Fe}}{\text{55}\text{.85 g}}=\text{0}\text{.659 mol Fe} \\ & n_{\text{S}}=\text{21}\text{.1 g}\times \frac{\text{1 mol S}}{\text{32}\text{.1 g}}=\text{0}\text{.657 mol S} \\ & n_{\text{O}}=\text{42}\text{.1 g}\times \frac{\text{1 mol O}}{\text{16}\text{.01 g}}=\text{2}\text{.63 mol O} \\ \end{align}\) The ratio is\(\frac{n_{\text{S}}}{n_{\text{Fe}}}=\frac{\text{0}\text{.657 mol S}}{\text{0}\text{.659 mol Fe}}=\frac{\text{1}\text{.00 mol S}}{\text{1 mol Fe}}\)
\(\frac{n_{\text{O}}}{n_{\text{Fe}}}=\frac{\text{2}\text{.63 mol O}}{\text{0}\text{.659 mol Fe}}=\frac{\text{3}\text{.99 mol O}}{\text{1 mol Fe}}\)
We would therefore assign the formula FeSO4 , and the balanced equation for the synthesis is:
- 2 FeS2 + 7 O2 + 2 H2O → 2 FeSO4 + 2 H2SO4
Empirical and Molecular Formulas
As we'll see in the next example, our method can only determine the ratio of elements in a compound.
Dextran, a polymer whose structure is shown below, is commonly used to complex Fe2+ ion to make injectible iron supplements, like INFeD® [3]. Suppose a sample of an iron dextran complex has a molecular mass of 450, and contains 32.0% C, 4.00% H, 24.8 % Fe and 39.1 % O. Determine its empirical and molecular formulas.

Dextran monomers
Solution
\(\begin{align} & n_{\text{C}}=\text{32}\text{.0 g}\times \frac{\text{1 mol C}}{\text{12}\text{.01 g}}=\text{2}\text{.66 mol C} \\ & n_{\text{H}}=\text{4}\text{.00 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{4}\text{.00 mol H} \\ & n_{\text{O}}=\text{39}\text{.1 g}\times \frac{\text{1 mol O}}{\text{15}\text{.999 g}}=\text{2}\text{.44 mol O} \\ & n_{\text{Fe}}=\text{24}\text{.8 g}\times \frac{\text{1 mol Fe}}{\text{55}\text{.845 g}}=\text{0}\text{.444 mol Fe} \\ \end{align}\)
\(\frac{n_{\text{H}}}{n_{\text{Fe}}}=\frac{\text{4}\text{.00 mol H}}{\text{0}\text{.444 mol Fe}}=\frac{\text{9}\text{.01 mol H}}{\text{1 mol Fe}}\)
\(\frac{n_{\text{C}}}{n_{\text{Fe}}}=\frac{\text{2}\text{.66 mol C}}{\text{0}\text{.444 mol Fe}}=\frac{\text{5}\text{.99 mol C}}{\text{1 mol Fe}}\)
\(\frac{n_{\text{O}}}{n_{\text{Fe}}}=\frac{\text{2}\text{.44 mol O}}{\text{0}\text{.444 mol Fe}}=\frac{\text{5}\text{.5 mol O}}{\text{1 mol Fe}}\)
The ratios C6H9O5.5Fe1 are the same as the ratios C12H18O11Fe2. or C24H36O22Fe4.
Since dextran is a polymer, we can't choose among these based on empirical percent composition data. The formula determined by this method is called the empirical formula or simplest formula: C6H9O5.5Fe1.
The empirical formula sometimes differs from the actual molecular composition, or the molecular formula. Experimental determination of the molecular weight in addition to percent composition permits calculation of the molecular formula, and the molecular weight is given above as 450.
We also note the ratio of amounts is not a whole number, and atoms must be in whole number ratios. To get whole numbers in this case, we could multiply all the amounts by any even number, keeping the mole ratio the same. We'll just calculate the empirical formula mass, and see what the multiplier is:
The molecular weight corresponding to the empirical formula is
(6 × 12.01) + (9 × 1.008) + (5.5 × 16) + (1 × 55.846) = 225
Since the experimental molecular weight is twice as great, all subscripts must be doubled and the molecular formula is C12H18O11Fe2.
It may be less obvious how to convert some mole ratios to whole numbers. Suppose the ratio of amounts of carbon to oxygen, for example, were 2.25:1, and we're sure enough of the analysis to know that it's not 2.33:1 or 2.50:1. We must convert 2.25 to a ratio of small whole numbers. This can be done by changing the figures after the decimal point to a fraction. In this case, .25 becomes ¼. Thus 2.25 = 2¼ = \(\tfrac{\text{9}}{\text{4}}\), and
\(\frac{n_{\text{C}}}{n_{\text{O}}}=\frac{\text{2}\text{.25 mol C}}{\text{1 mol O}}=\frac{\text{9 mol C}}{\text{4 mol O}}\)
Determining Weight Percent from the Formula
HIP, Ferrous Fumarate, and Ferrous Sulfate
Once someone has determined a formula–empirical or molecular—it is possible to do the reverse calculation. Finding the weight-percent composition from the formula often proves quite informative, as the following example shows.
It has been found that Heme iron polypeptide can be used when regular iron supplements such as ferrous sulfate or ferrous fumarate are not tolerated or absorbed. A clinical study demonstrated that HIP increased serum iron levels 23 times greater than ferrous fumarate on a milligram-per-milligram basis.[3][4]HIP contains the central unit of hemoglobin in animal flesh, possibly with attached proteins.
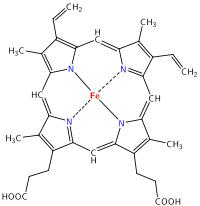
HIP core
Since this molecule contains a much smaller percent iron than Ferrous sulfate, it is amazing that the iron is 23 time more bioavailable. Let's analyze these data.
Elemental analysis: 66.24%C, 5.23%H, 9.09%N
HIP, C34H32O4FeN4 (Molecular weight: 616.498), Ferrous sulfate, FeSO4, and Ferrous fumarate, C4H2FeO4 Molecular weight: 169.9, all are used as iron supplements. Which has the highest percent of iron?
Solution
We will show the detailed calculation only for the case of C4H2FeO4
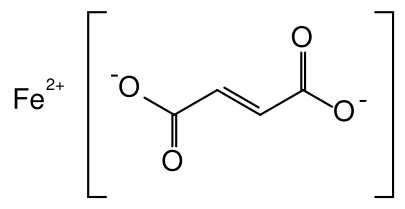
Iron Fumarate
1 mol C4H2FeO4 contains 4 mol C, 2 mol H, and 4 mol O, and 1 mol Fe. The molar mass is thus
M = (4 × 12.0 + 2 × 1.008 + 4 × 16.00 + 1 × 55.85) g mol–1 = 169.9 g mol–1
A 1-mol sample would weigh 169.9 g. The mass of 4 mol C it contains is \(m_{\text{C}}\text{ = 4 mol C }\times \text{ }\frac{\text{12}\text{.0 g}}{\text{1 mol C}}\text{ = 48}\text{.0 g}\) Therefore the percentage of C is \(\text{ }\!\!%\!\!\text{ C = }\frac{m_{\text{C}}}{m_{\text{C}_{\text{4}}\text{H}_{\text{2}}\text{O}_{\text{4}}\text{Fe}_{\text{1}}}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = }\frac{\text{48}\text{.0 g}}{\text{169}\text{.9 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 28}\text{.3 }\!\!%\!\!\text{ }\) The percentages of H, Fe, and O are easily calculated as \(\begin{align} & m_{\text{H}}\text{ = 2 mol H }\times \text{ = }\frac{\text{1}\text{.008 g}}{\text{1 mol H}}\text{ = 2}\text{.016 g} \\ & \text{ }\!\!%\!\!\text{ H = }\frac{\text{2}\text{.016 g}}{\text{169}\text{.9 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 1}\text{.19 }\!\!%\!\!\text{ } \\ #10; & m_{\text{O}}\text{ = 4 mol O }\times \text{ = }\frac{\text{16}\text{.00 g}}{\text{1 mol O}}\text{ = 64}\text{.00 g} \\ & \text{ }\!\!%\!\!\text{ O = }\frac{\text{64}\text{.00 g}}{\text{169}\text{.9 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 37}\text{.7 }\!\!%\!\!\text{ } \\ & m_{\text{Fe}}\text{ = 1 mol O }\times \text{ = }\frac{\text{55}\text{.85 g}}{\text{1 mol Fe}}\text{ = 55}\text{.85 g} \\ & \text{ }\!\!%\!\!\text{ Fe = }\frac{\text{55}\text{.85 g}}{\text{169}\text{.9 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 32}\text{.97 }\!\!%\!\!\text{ } \\ \end{align}\)
Though not strictly needed to answer the problem, the percentages of C, H, and O provide a check of the results. The total 28.3 + 1.19% + 37.7% + 32.97% = 100.00% as it should.
Similar calculations for FeSO4, and HIP yield 36.8% and 9.1% iron, respectively. It's amazing that the HIP with only 9.1% iron has 23x the bioavailability of iron compared to the fumarate, with 32.97% iron. Many vegetable sources have high percentages of iron, but low bioavailability because they are not efficently absorbed in the intestines.
References
- www.irontoxicity.com/hcp/consequences.jsp
- en.Wikipedia.org/wiki/Iron_poisoning
- www.infed.com/
- Seligman, et al., Nutritional Research 2000; Vol. 20, No 9:1279-1286.


