2.12.2: Environment- Fertilizers, Formulas, and Ecological Stoichiometry
- Page ID
- 50713
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Fertilizers, Formulas and Ecological Stoichiometry
Fertilizer Composition
When you shop for fertilizers, you will find them labeled according to the "NPK" (nitrogen/phosphorus/potassium) analysis. For example, one fertilizer might be labeled "18-51-20".
Deciphering this label requires understanding of chemical formulas.
The nitrogen value (18) is the actual percent nitrogen in the fertilizer, but the phosphorus and potassium values are not.

Phosphorus Content
The phosphorus content is actually expressed as if the phosphorus compound were P2O5. So the "51" in the label means 51% P2O5.
But what percent of this is actually phosphorus itself?
We can determine that from the formula.
EXAMPLE 1 Determine the percent phosphorus and the percent oxygen in P2O5.
Solution The formula indicates the relative amounts (in mol) of phosphorus and oxygen, so 1 mol of the compound contains 2 mol of P and 5 mol of O.
The percent phosphorus is
\(\text{ }\!\!%\!\!\text{ P = }\frac{m_{\text{P}}}{m_{\text{compound}}}\text{ }\times \text{ 100 }\!\!%\!\!\)
1 mol of P2O5 has a mass of (2 mol P * 31 g/mol P + 5 mol O * (16.0 g/mol O) = 142 g, and it contains 2 mol of P, weighing 2 mol P * 31.0 g/mol = 62.0 g, so...
\(\text{ }\!\!%\!\!\text{ P = }\frac{m_{\text{P}}}{m_{\text{P}_{\text{2}}\text{O}_{\text{5}}}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = }\frac{\text{62}\text{.0 g}}{\text{142}\text{.0 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 43}\text{.7 }\!\!%\!\!\text{ }\)
Similarly,
%O = 100% x (5 mol O * 16 g/mol) / (2 mol P * 31 g/mol P + 5 mol O * (16.0 g/mol O)
% O = 56.3%
If the fertilizer contains 51% P2O5, it contains only 43.7% of that as pure phosphorus, or 0.437 * 51 = 22.3% P.
How does an analytical laboratory determine which phosphorus compound is present? First, the compound must be separated from the others and purified, possibly by dissolving it in a solvent that does not dissolve the others, then evaporating the solvent until the compound "recrystallizes". Then techniques of quantitative analysis are used to determine the percentage by mass of each element in the compound. Such data are usually reported as the percent composition.
EXAMPLE 2 When 10.0 g of phosphorus burns in oxygen, 22.9 g of a pure compound is formed. Calculate the percent composition from these experimental data.
Solution The percentage of phosphorus is the mass of phosphorus divided by the total mass of compound times 100 percent:
\(\text{ }\!\!%\!\!\text{ P = }\frac{m_{\text{P}}}{m_{\text{compound}}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = }\frac{\text{10}\text{.0 g}}{\text{22}\text{.9 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 43}\text{.7 }\!\!%\!\!\text{ }\) The remainder of the compound (22.9 g – 10 g = 12.9 g) is oxygen: \(\text{ }\!\!%\!\!\text{ O = }\frac{m_{\text{O}}}{m_{\text{compound}}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = }\frac{\text{12}\text{.9 g}}{\text{22}\text{.9 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 56}\text{.3 }\!\!%\!\!\text{ }\) As a check, verify that the percentages add to 100: 56.3% + 43.7% = 100%
Potassium Content
The potassium (K) content of a fertilizer is actually expressed as if the potassium compound were K2O. So the "20" in the label (above) means 20% K2O, which is 17% oxygen and 83% elemental potassium:
% K = 100% x m (K, g) / m (Total, g) = (2 mol K * 39.1 g/mol) / (2 mol K * 39.1 g/mol + 1 mol O * 16.0 g/mol)
So the true percentage of potassium in the fertilizer is 0.83 x % K2O = 0.83 x 20% = 16.6% K
So 18−51−20 fertilizer actually contains (by weight) 18% elemental (N), 22% elemental (P), and 16% elemental (K).
Ecological Stoichiometry and the Growth Rate Hypothesis
Ecological stoichiometry is an approach to ecology which studies how the chemical elements in a population of plants or animals matches the elements in the food supply for the population. Most plants and animals (including us) show a high degree of chemical hormesis, that is, they have a characteristic chemical composition regardless of their environment, or food supply. They need food which supplies the elements in the proper ratios.
If we want plants to grow well, we need to supply elements in the proper ratios.
One claim of the practitioners of ecological stoichiometry is that fast growth requires high concentrations of RNA, which in turn requires a lot of phosphorus. This is the "Growth Rate Hypothesis" [1] [2].
Nutrient Ratios
The nitrogen to phosphorus ratio in RNA is similar to that in ATP, which is one of its constituents (along with UTP, CTP and GTP). Suppose that this N:P ratio establishes the requirements for the plant. We can then calculate the optimal N:P food ratio by calculating the N:P ratio in ATP, whose structure is:
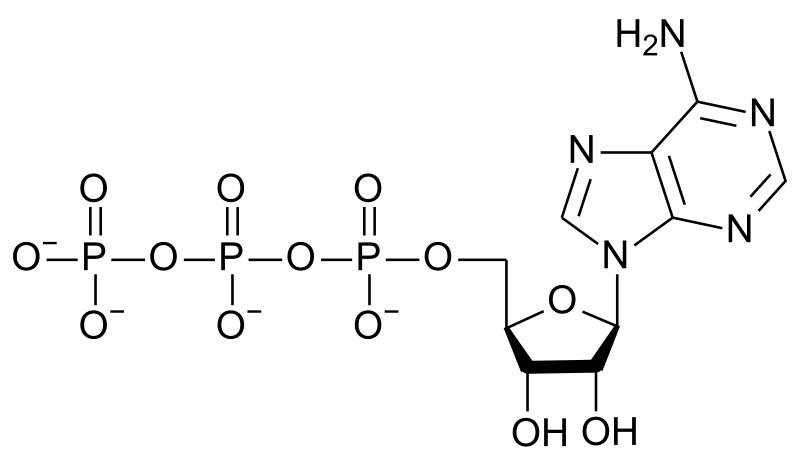
From the formula, C10H16N5O13P3,we see that % N = 100* (5*14.0 / 507.2 ) = 13.8%
%P = 100* (3*31 / 507.2) = 18.3% P
So the optimal N/P ratio is 13.8/18.3 = 0.753:1
Is the 18−51−20 fertilizer optimal for ATP synthesis in the plant? The N:P ratio is 18/51 = 0.35, much less than that required. This particular fertilizer is designed for soils that are depleted in phosphorus.
Ecological stoichiometry focuses on the chemical requirements of each trophic level, in addition to energy requirements. Proponents say that "Ecological stoichiometry recognizes that organisms themselves are outcomes of chemical reactions and thus their growth and reproduction can be constrained by supplies of key chemical elements [especially carbon (C), nitrogen (N) and phosphorus (P)]".[3]. Organisms in each trophic level of an ecosystem must have evolved to utilize the nutrient ratios provided by the lower trophic levels.
Formulas from Percent Composition
To obtain the formula from percent-composition data for a phosphorus oxide, we must find how many phosphorus atoms there are per oxygen atom. On a macroscopic scale this corresponds to the ratio of the amount of phosphorus to the amount of oxygen. If the formula is P2O5, it not only indicates that there are five oxygen atoms for every two phosphorus atoms, it also says that there are 5 mol of oxygen atoms for each 2 mol of phosphorus atoms. That is, the amount of oxygen is 2.5 times the amount of phosphorus. The numbers in the ratio of the amount of phosphorus to the amount of oxygen (2:5) are the subscripts of phosphorus and oxygen in the formula.
EXAMPLE 3 Phosphorus forms several oxides, including phosphorus pentoxide, P2O5, phosphorus trioxide, P2O3, P4O7, P4O8, P4O9, PO and P2O6. Determine the formula for the compound whose percent phosphorus is 49.2%.
Solution For convenience, assume that we have 100 g of the compound. Of this, 49.2 g (49.2%) is phosphorus and 50.8 g is oxygen (100% - 49.2%). Each mass can be converted to an amount of substance
\(\begin{align} & n_{\text{P}}=\text{49}\text{.2 g}\times \frac{\text{1 mol P}}{\text{31}\text{.0 g}}=\text{1}\text{.59 mol P} \\ & n_{\text{O}}=\text{50}\text{.8 g}\times \frac{\text{1 mol O}}{\text{16}\text{.0 g}}=\text{3}\text{.18 mol O} \\ \end{align}\) Dividing the larger amount by the smaller, we have \(\frac{n_{\text{O}}}{n_{\text{P}}}=\frac{\text{3}\text{.18 mol O}}{\text{1}\text{.59 mol P}}=\frac{\text{2}\text{.00 mol O}}{\text{1 mol P}}\) The ratio 2.0 mol O to 1 mol P also implies that there are 2.00 O atoms per 1 P atom. Therefore we write the formula as PO2.
This is the "Empirical Formula", and it gives the smallest ratio of atoms. The "molecular formula" could be twice as large, P2O4, or some other multiple of the empirical formula. In this case, the known oxide with the 1:2 ratio is PO4O8.
Occasionally the ratio of amounts is not a whole number.
EXAMPLE 5 Aspirin contains 60.0% C, 4.48% H, and 35.5% O. What is its empirical formula?
Solution
\(\begin{align} & n_{\text{H}}=\text{14}\text{.4 g}\times \frac{\text{1 mol H}}{\text{1}\text{.008 g}}=\text{14}\text{.3 mol H} \\ & n_{\text{C}}=\text{85}\text{.6 g}\times \frac{\text{1 mol C}}{\text{12}\text{.01 g}}=\text{7}\text{.13 mol C} \\ & n_{\text{O}}=\text{35}\text{.5 g}\times \frac{\text{1 mol O}}{\text{16}\text{.00 g}}=\text{2}\text{.22 mol O} \\ \end{align}\) Divide all three by the smallest amount of substance \(\begin{align} & \frac{n_{\text{C}}}{n_{\text{O}}}=\frac{\text{5}\text{.00 mol C}}{\text{2}\text{.22 mol O}}=\frac{\text{2}\text{.25 mol H}}{\text{1 mol O}} \\ & \frac{n_{\text{H}}}{n_{\text{O}}}=\frac{\text{4}\text{.44 mol H}}{\text{2}\text{.22 mol O}}=\frac{\text{2}\text{.00 mol H}}{\text{1 mol O}} \\ \end{align}\) Clearly there are twice as many H atoms as O atoms, but the ratio of C to O is not so obvious. We must convert 2.25 to a ratio of small whole numbers. This can be done by changing the figures after the decimal point to a fraction. In this case, .25 becomes ¼. Thus 2.25 = 2¼ = \(\tfrac{\text{9}}{\text{4}}\), and \(\frac{n_{\text{C}}}{n_{\text{O}}}=\frac{\text{2}\text{.25 mol C}}{\text{1 mol O}}=\frac{\text{9 mol C}}{\text{4 mol O}}\) We can also write \(\frac{n_{\text{H}}}{n_{\text{O}}}=\frac{\text{2 mol H}}{\text{1 mol O}}=\frac{\text{8 mol H}}{\text{4 mol O}}\) Thus the empirical formula is C9H8O4.
Once someone has determined a formula–empirical or molecular—it is possible for someone else to do the reverse calculation. Finding the weight-percent composition from the formula often proves quite informative, as the following example shows.
EXAMPLE 6 In order to replenish nitrogen removed from the soil when plants are harvested, the compounds NaNO3 (sodium nitrate), NH4NO3 (ammonium nitrate), and NH3 (ammonia) are used as fertilizers. If a farmer could buy each at the same cost per gram, which would be the best bargain? In other words, which compound contains the largest percentage of nitrogen?
Solution We will show the detailed calculation only for the case of NH4NO3.
1 mol NH4NO3 contains 2 mol N, 4 mol H, and 3 mol O. The molar mass is thus M = (2 × 14.01 + 4 × 1.008 + 3 × 16.00) g mol–1 = 80.05 g mol–1 A 1-mol sample would weigh 80.05 g. The mass of 2 mol N it contains is \(m_{\text{N}}\text{ = 2 mol N }\times \text{ }\frac{\text{14}\text{.01 g}}{\text{1 mol N}}\text{ = 28}\text{.02 g}\) Therefore the percentage of N is \(\text{ }\!\!%\!\!\text{ N = }\frac{m_{\text{N}}}{m_{\text{NH}_{\text{4}}\text{NO}_{\text{3}}}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = }\frac{\text{28}\text{.02 g}}{\text{80}\text{.05 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 35}\text{.00 }\!\!%\!\!\text{ }\) The percentages of H and O are easily calculated as \(\begin{align} & m_{\text{H}}\text{ = 4 mol H }\times \text{ = }\frac{\text{1}\text{.008 g}}{\text{1 mol H}}\text{ = 4}\text{.032 g} \\ & \text{ }\!\!%\!\!\text{ H = }\frac{\text{4}\text{.032 g}}{\text{80}\text{.05 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 5}\text{.04 }\!\!%\!\!\text{ } \\ & m_{\text{O}}\text{ = 3 mol O }\times \text{ = }\frac{\text{16}\text{.00 g}}{\text{1 mol O}}\text{ = 48}\text{.00 g} \\ & \text{ }\!\!%\!\!\text{ O = }\frac{\text{48}\text{.00 g}}{\text{80}\text{.05 g}}\text{ }\times \text{ 100 }\!\!%\!\!\text{ = 59}\text{.96 }\!\!%\!\!\text{ } \\ \end{align}\) Though not strictly needed to answer the problem, the latter two percentages provide a check of the results. The total 35.00 + 5.04% + 59.96% = 100.00% as it should. Similar calculations for NaNO3 and NH3 yield 16.48% and 82.24% nitrogen, respectively. The farmer who knows chemistry chooses ammonia!
References
- Ecological Stoichiometry: The Biology of elements from Molecules to Biosphere; Robert W. Sterner and James J. Elser; Princeton University Press, Princeton, NJ, 2002.
- en.Wikipedia.org/wiki/Ecological_stoichiometry
- Plos Biology [www.plosbiology.org]


