11.4: Equilibrium Expressions

Learning Objectives

Make sure you thoroughly understand the following essential ideas:

• The equilibrium quotient Q is the value of the equilibrium expression of a reaction for any arbitrary set of concentrations or partial pressures of the reaction components.
• The equilibrium constant K is the value of Q when the reaction is at equilibrium. K has a unique value for a given reaction at a fixed temperature and pressure.
• Q and K can be expressed in terms of concentrations, partial pressures, or, when appropriate, in some combination of these.
• For a reaction in which all the components are gases, Q_c and K_c will have different values except in the special case in which the total number of moles of gas does not change.
• Concentration terms for substances whose concentrations do not change in the reaction do not appear in equilibrium expressions. The most common examples are [H₂O] when the reaction takes place in aqueous solution (so that [H₂O] is effectively constant at 55.6 M), and in heterogeneous reactions involving solids, in which the concentration of the solid is determined by the density of the solid itself.
• A reaction whose equilibrium constant is in the range of about 0.01 to 100 is said to be incomplete or [thermodynamically] reversible.
• Q and K are conventionally treated as dimensionless quantities, and need not ordinarily have units associated with them.
• Heterogeneous reactions are those in which two or more phases are involved; homogeneous reactions take place in a single phase. A common type of heterogeneous reaction is the loss of water of crystallization by a solid hydrate such as CuSO₄·5H₂O.
• The equilibrium expression can be manipulated and combined in the following ways:
  • If the reaction is written in reverse, Q becomes Q^–1;
  • If the coefficients of an equation are multiplied by n, Q becomes Qⁿ;
  • Q for the sum of two reactions (that is, for two reactions that take place in sequence) is the product (Q₁)(Q₂).

You know that an equilibrium constant expression looks something like K = [products] / [reactants]. But how do you translate this into a format that relates to the actual chemical system you are interested in? This lesson will show you how to write the equilibrium constant expressions that you will need to use when dealing with the equilibrium calculation problems in the chapter that follows this one.

Pressures can Express Concentrations

Although we commonly write equilibrium quotients and equilibrium constants in terms of molar concentrations, any concentration-like term can be used, including mole fraction and molality. Sometimes the symbols \(K_c\) , \(K_x\) , and \(K_m\) are used to denote these forms of the equilibrium constant. Bear in mind that the numerical values of K’s and Q’s expressed in these different ways will not generally be the same.

Most of the equilibria we deal with in this course occur in liquid solutions and gaseous mixtures. We can express \(K_c\) values in terms of moles per liter for both, but when dealing with gases it is often more convenient to use partial pressures. These two measures of concentration are of course directly proportional:

\[c=\dfrac{n}{V}=\dfrac{\dfrac{PV}{RT}}{V}=\dfrac{P}{RT} \label{Eq1}\]

so for a reaction \(A_{(g)} \rightarrow B_{(g)}\) we can write the equilibrium constant as

\[K_p =\dfrac{P_B}{P_A} \label{Eq2}\]

Owing to interactions between molecules, especially when ions are involved, all of these forms of the equilibrium constant are only approximately correct, working best at low concentrations or pressures. The only equilibrium constant that is truly “constant” (except that it still varies with the temperature!) is expressed in terms of activities, which you can think of as “effective concentrations” that allow for interactions between molecules. In practice, this distinction only becomes important for equilibria involving gases at very high pressures (such as are often encountered in chemical engineering) and in ionic solutions more concentrated than about 0.001 M. We will not deal much with activities in this course.

For a reaction such as

\[CO_{2\, (g)} + OH^–_{(aq)} \rightleftharpoons HCO_{3\, (aq)}^- \label{Eq3}\]

that involves both gaseous and dissolved components, a “hybrid” equilibrium constant is commonly used:

\[ K =\dfrac{[HCO_3^-]}{P_{CO_2}[OH^-]} \label{Eq4}\]

Clearly, it is essential to be sure of the units when you see an equilibrium constant represented simply by "\(K\)".

A note about pressure and concentration units

In this lesson (and in most of the others in this set,) we express concentrations in mol L^–1 and pressures in atmospheres. Although this reflects common usage among chemists (older ones, especially!), these units are not part of the SI system which has been the international standard since the latter part of the 20th Century.

Molar concentrations are now more properly expressed in mol dm^–3 and the "standard atmosphere" corresponds to a pressure of 101.325 kPa. Until 1990, 1 atm was the "standard pressure" employed in calculations involving the gas laws, and also in thermodynamics. Since that date, "standard pressure" has been 100.000 kPa, also expressed as 1 bar.

For most practical purposes, the differences between these values are so small that they can be neglected.

Converting between \(K_p\) and \(K_c\)

It is sometimes necessary to convert between equilibrium constants expressed in different units. The most common case involves pressure- and concentration equilibrium constants. Note that when V is expressed in liters and P in atmospheres, R must have the value 0.08206 L-atm/mol K.). The ideal gas law relates the partial pressure of a gas to the number of moles and its volume:

\[PV = nRT \]

Concentrations are expressed in moles/unit volume n/V, so by rearranging the above equation we obtain the explicit relation of pressure to concentration:

\[P = \left(\dfrac{n}{V} \right)RT \label{Eq5}\]

Conversely,

\[c = \dfrac{n}{V} = \dfrac{P}{RT}\]

so a concentration of a gas [A] can be expressed as \(\dfrac{P_A}{RT}\).

For a reaction of the form \(A + 3 B\rightleftharpoons 2C\), we can write

Assuming that all of the components are gases, the difference

\[(\text{moles of gas in products}) – (\text{moles of gas in reactants}) = \Delta{n_g} \nonumber\]

is given by

\[ \color{red} {K_p = K_c (RT)^{\Delta{n_g}} \label{Eq6}}\]

Do not show unchanging concentrations!

Substances whose concentrations undergo no significant change in a chemical reaction do not appear in equilibrium constant expressions. How can the concentration of a reactant or product not change when a reaction involving that substance takes place? There are two general cases to consider.

The substance is also the Solvent

This happens all the time in acid-base chemistry. Thus for the hydrolysis of the cyanide ion

\[\ce{CN^{-} + H2O <=> HCN + OH^{–}} \nonumber\]

we write

\[K_c= \dfrac{[\ce{HCN}][\ce{OH^-}]}{[\ce{CN^-}]} \nonumber\]

in which no \([H_2O]\) term appears. The justification for this omission is that water is both the solvent and reactant, but only the tiny portion that acts as a reactant would ordinarily go in the equilibrium expression. The amount of water consumed in the reaction is so minute (because \(K\) is very small) that any change in the concentration of \(H_2O\) from that of pure water (55.6 mol L^–1) will be negligible.

Similarly, for the "autodissociation" of water

\[H_2O = H^+ + OH^– \nonumber\]

the equilibrium constant is expressed as the "ion product"

\[K_w = [H^+][OH^–] \nonumber\]

Be careful about throwing away H₂O whenever you see it. In the esterification reaction

\[\ce{CH3COOH + C2H5OH <=> CH3COOC2H5 + H2O} \nonumber\]

that we discussed in a previous section, a [H₂O] term must be present in the equilibrium expression if the reaction is assumed to be between the two liquids acetic acid and ethanol. If, on the other hand, the reaction takes place between a dilute aqueous solution of the acid and the alcohol, then the [H₂O] term would not be included.

The substance is a solid or a pure liquid phase

This is most frequently seen in solubility equilibria, but there are many other reactions in which solids are directly involved:

\[CaF_{2\, (s)} \rightarrow Ca^{2+}_{(aq)} + 2F^-_{(aq)} \label{Eq11}\]

\[Fe_3O_4(s) + 4 H_{2\, (g)} \rightarrow 4 H_2O_{(g)} + 3Fe_{(s)} \label{Eq12}\]

These are heterogeneous reactions (meaning reactions in which some components are in different phases), and the argument here is that concentration is only meaningful when applied to a substance within a single phase.

Thus the term \([CaF_2]\) would refer to the “concentration of calcium fluoride within the solid \(CaF_2\)", which is a constant depending on the molar mass of \(CaF_2\) and the density of that solid. The concentrations of the two ions will be independent of the quantity of solid \(CaF_2\) in contact with the water; in other words, the system can be in equilibrium as long as any \(CaF_2\) at all is present. Throwing out the constant-concentration terms can lead to some rather sparse-looking equilibrium expressions. For example, the equilibrium expression for each of the processes shown in the following table consists solely of a single term involving the partial pressure of a gas:

Table \(\PageIndex{1}\):

\(CaCO_{3(s)} \rightleftharpoons CaO_{(s)} + CO_{2(g)}\)	\(K_p = P_{CO_2}\)	Thermal decomposition of limestone, a first step in the manufacture of cement.
\(Na_2SO_4 \cdot 10 H_2O_{(s)} Na_2SO_{4(s)} + 10 H_2O_{(g)}\)	\(K_p = P_{H_2O}^{10}\)	Sodium sulfate decahydrate is a solid in which H2O molecules (“waters of hydration") are incorporated into the crystal structure.)
\(I_{2(s)} \rightleftharpoons I_{2(g)}\)	\(K_p = P_{I_2}\)	sublimation of solid iodine; this is the source of the purple vapor you can see above solid iodine in a closed container.
\(H_2O_{(l)} \rightleftharpoons H_2O_{(g)}\)	\(K_p = P_{H_2O}\)	Vaporization of water. When the partial pressure of water vapor in the air is equal to K, the relative humidity is 100%.

The last two processes represent changes of state (phase changes) which can be treated exactly the same as chemical reactions. In each of the heterogeneous processes shown in Table \(\PageIndex{1}\), the reactants and products can be in equilibrium (that is, permanently coexist) only when the partial pressure of the gaseous product has the value consistent with the indicated \(K_p\). Bear in mind also that these \(K_p\)'s all increase with the temperature.

Example \(\PageIndex{1}\)

What are the values of \(K_p\) for the equilibrium between liquid water and its vapor at 25°C, 100°C, and 120°C? The vapor pressure of water at these three temperatures is 23.8 torr, 760 torr (1 atm), and 1489 torr, respectively.

Comment: These vapor pressures are the partial pressures of water vapor in equilibrium with the liquid, so they are identical with the \(K_p\)'s when expressed in units of atmospheres.

Solution

25°C

100°C

120°C

\(K_p = \dfrac{23.8\; torr}{ 760\; torr/atm} = 0.031\; atm\) \(K_p = 1.00\; atm\) \(K_p = \dfrac{1489\; torr}{ 760\; torr/atm} = 1.96\; atm\) The partial pressure of H2O above the surface of liquid water in a closed container at 25°C will build up to this value. If the cover is removed so that this pressure cannot be maintained, the system will cease to be at equilibrium and the water will evaporate.

This temperature corresponds, of course, to the boiling point of water. The normal boiling point of a liquid is the temperature at which the partial pressure of its vapor is 1 atm.

The only way to heat water above its normal boiling point is to do so in a closed container that can withstand the increased vapor pressure. Thus a pressure cooker that operates at 120°C must be designed to withstand an internal pressure of at least 2 atm.

Values of Equilibrium Constants

or “reversible”.

As an equilibrium constant approaches the limits of zero or infinity, the reaction can be increasingly characterized as a one-way process; we say it is “complete” or “irreversible”. The latter term must of course not be taken literally; the Le Chatelier principle still applies (especially insofar as temperature is concerned), but addition or removal of reactants or products will have less effect.

Kinetically Hindered Reactions

Although it is by no means a general rule, it frequently happens that reactions having very large equilibrium constants are kinetically hindered, often to the extent that the reaction essentially does not take place.

The examples in the following table are intended to show that numbers (values of K), no matter how dull they may look, do have practical consequences!

Table \(\PageIndex{2}\): Examples of Reversible Reactions

Reaction	K	remarks
\(N_{2(g)} + O_{2(g)} \rightleftharpoons 2 NO_{(g)}\)	\(5 \times 10^{–31}\) at 25°C, 0.0013 at 2100°C	These two very different values of K illustrate very nicely why reducing combustion-chamber temperatures in automobile engines is environmentally friendly.
\(3 H_{2(g)} + N_{2(g)} \rightleftharpoons 2 NH_{3(g)}\)	\(7 \times 10^5\) at 25°C, 56 at 1300°C	See the discussion of this reaction in the section on the Haber process.
\(H_{2(g)} \rightleftharpoons 2 H_{(g)}\)	\(10^{–36}\) at 25°C, \(6 \times 10^{–5}\) at 5000°	Dissociation of any stable molecule into its atoms is endothermic. This means that all molecules will decompose at sufficiently high temperatures.
\(H_2O_{(g)} \rightleftharpoons H_{2(g)} + ½ O_{2(g)}\)	\(8 \times 10^{–41}\) at 25°C	You won’t find water a very good source of oxygen gas at ordinary temperatures!
\(CH_3COOH_{(l)} \rightleftharpoons 2 H_2O_{(l)} + 2 C_{(s)}\)	\(K_c = 10^{13}\) at 25°C	This tells us that acetic acid has a great tendency to decompose to carbon, but nobody has ever found graphite (or diamonds!) forming in a bottle of vinegar. A good example of a super kinetically-hindered reaction!

Do Equilibrium Constants have Units?

The equilibrium expression for the synthesis of ammonia

\[3 H_{2(g)} + N_{2(g)} \rightarrow 2 NH_{3(g)} \label{Eq13}\]

can be expressed as

\[ K_p =\dfrac{P^2_{NH_3}}{P_{N_2}P^3_{H_2}} \label{Eq14}\]

or

\[ K_c = \dfrac{[NH_3]^2}{[N_2] [H_2]^3} \label{Eq15}\]

so \(K_p\) for this process would appear to have units of atm^–1, and \(K_c\) would be expressed in mol^–2 L². And yet these quantities are often represented as being dimensionless. Which is correct? The answer is that both forms are acceptable. There are some situations (which you will encounter later) in which K’s must be considered dimensionless, but in simply quoting the value of an equilibrium constant it is permissible to include the units, and this may even be useful in order to remove any doubt about the units of the individual terms in equilibrium expressions containing both pressure and concentration terms. In carrying out your own calculations, however, there is rarely any real need to show the units.

Strictly speaking, equilibrium expressions do not have units because the concentration or pressure terms that go into them are really ratios having the forms (n mol L^–1)/(1 mol L^–1) or (n atm)/(1 atm) in which the unit quantity in the denominator refers to the standard state of the substance; thus the units always cancel out. (But first-year students are not expected to know this!)

For substances that are liquids or solids, the standard state is just the concentration of the substance within the liquid or solid, so for something like CaF(s), the term going into the equilibrium expression is [CaF₂]/[CaF₂] which cancels to unity; this is the reason we don’t need to include terms for solid or liquid phases in equilibrium expressions. The subject of standard states would take us beyond where we need to be at this point in the course, so we will simply say that the concept is made necessary by the fact that energy, which ultimately governs chemical change, is always relative to some arbitrarily defined zero value which, for chemical substances, is the standard state.

How the Reaction Equation affects K

It is important to remember that an equilibrium quotient or constant is always tied to a specific chemical equation, and if we write the equation in reverse or multiply its coefficients by a common factor, the value of \(Q\) or \(K\) will change. The rules are very simple:

• Writing the equation in reverse will invert the equilibrium expression;
• Multiplying the coefficients by a common factor will raise Q or K to the corresponding power.

Here are some of the possibilities for the reaction involving the equilibrium between gaseous water and its elements:

Example 1: \(\ce{2 H2 + O2 <=> 2 H2O} \) with equilibrium expression \[K_p = \dfrac{P_{H_2O}^2}{P_{H_2}^2P_{O_2}} \nonumber\]

Example 2: \(\ce{10 H2 + 5 O2 <=> 10 H2O}\) with equilibrium expression \[\begin{align*} K_p &= \dfrac{P_{H_2O}^{10}}{P_{H_2}^{10}P_{O_2}^5} \\[4pt] &= \left(\dfrac{P_{H_2O}^2}{P_{H_2}^2P_{O_2}}\right)^{5}\end{align*}\]

Example 3: \(\ce{H2 + 1/2 O2 <=> H2O} \) with equilibrium expression \[\begin{align*} K_p &= \dfrac{P_{H_2O}}{P_{H_2}P_{O_2}^{1/2}} \\[4pt] &= \left(\dfrac{P_{H_2O}^2}{P_{H_2}^2P_{O_2}}\right)^{1/2} \end{align*}\]

Example 4: \(\ce{H2O <=> H2 + 1/2 O2 } \) with equilibrium expression \[\begin{align*} K_p &= \dfrac{P_{H_2}P_{O_2}^{1/2}}{P_{H_2O}} \\[4pt] &= \left(\dfrac{P_{H_2O}^2}{P_{H_2}^2P_{O_2}}\right)^{-1/2} \end{align*}\]

Many chemical changes can be regarded as the sum or difference of two or more other reactions. If we know the equilibrium constants of the individual processes, we can easily calculate that for the overall reaction according to the following rule.

Multi-step Equilibria Rule

The equilibrium constant for the sum of two or more reactions is the product of the equilibrium constants for each of the steps.

Example \(\PageIndex{2}\)

Calculate the value of \(K\) for the reaction

\[\ce{CaCO3(s) + H^{+}(aq) <=> Ca^{2+}(aq) + HCO^{–}3(aq)} \nonumber\]

given the following equilibrium constants:

\(CaCO_{3(s)} \rightleftharpoons Ca^{2+}_{(aq)} + CO^{2–}_{3(aq)}\)	\(K_1 = 10^{–6.3}\)
\(HCO^–_{3(aq)} \rightleftharpoons H^+_{(aq)} + CO^{2–}_{3(aq)}\)	\(K_2 = 10^{–10.3}\)

Solution

The net reaction is the sum of reaction 1 and the reverse of reaction 2:

\(CaCO_{3(s)} \rightleftharpoons Ca^{2+}_{(aq)} + CO^{2–}_{3(aq)}\)	\(K_1 = 10^{–6.3}\)
\( H^+_{(aq)} + CO^{2–}_{3(aq)} \rightleftharpoons HCO^–_{3(aq)} \)	\(K_{–2} = 10^{–(–10.3)}\)
\(CaCO_{3(s)} + H^+_{(aq)} \rightarrow Ca^{2+}_{(aq)} + HCO^–_{3(aq)}\)	\(K = \dfrac{K_1}{K_2} = 10^{(-6.4+10.3)} =10^{+3.9}\)

Comment:

This net reaction describes the dissolution of limestone by acid; it is responsible for the eroding effect of acid rain on buildings and statues. This an example of a reaction that has practically no tendency to take place by itself (small K₁) being "driven" by a second reaction having a large equilibrium constant (K_–2). From the standpoint of the Le Chatelier principle, the first reaction is "pulled to the right" by the removal of carbonate by hydrogen ion. Coupled reactions of this type are widely encountered in all areas of chemistry, and especially in biochemistry, in which a dozen or so reactions may be linked.

Example \(\PageIndex{3}\)

The synthesis of \(\ce{HBr}\) from hydrogen and liquid bromine has an equilibrium constant \(K_p = 4.5 \times 10^{15}\) at 25°C. Given that the vapor pressure of liquid bromine is 0.28 atm, find \(K_p\) for the homogeneous gas-phase reaction at the same temperature.

Solution

The net reaction we seek is the sum of the heterogeneous synthesis of \(\ce{HBr}\) and the reverse of the vaporization of liquid bromine:

\(H_{2(g)} + Br_{2(l)} \rightleftharpoons 2 HBr_{(g)}\)	\(K_p = 4.5\times 10^{15}\)
\(Br_{2(g)} \rightleftharpoons Br_{2(l)}\)	\(K_p = (0.28)^{–1}\)
\(H_{2(g)} + Br_{2(g)} \rightleftharpoons 2 HBr_{(g)}\)	\(K_p = 1.6 \times 10^{16}\)

More on heterogeneous reactions

Heterogeneous reactions are those involving more than one phase. Some examples:

\(Fe(s) + O_2(g) \rightleftharpoons FeO_2(s)\)	air-oxidation of metallic iron (formation of rust)
\(CaF_2(s) \rightleftharpoons Ca(aq) + F^+(aq)\_	dissolution of calcium fluoride in water
\(H_2O(s) \rightleftharpoons H_2O(g)\)	sublimation of ice (a phase change)
\(NaHCO_3(s) + H^+(aq) \rightleftharpoons CO_2(g) + Na^+(aq) + H_2O(g)\)	formation of carbon dioxide gas from sodium bicarbonate when water is added to baking powder (the hydrogen ions come from tartaric acid, the other component of baking powder.)

The vapor pressure of solid hydrates

A particularly interesting type of heterogeneous reaction is one in which a solid is in equilibrium with a gas. The sublimation of ice illustrated in the above table is a very common example. The equilibrium constant for this process is simply the partial pressure of water vapor in equilibrium with the solid— the vapor pressure of the ice.

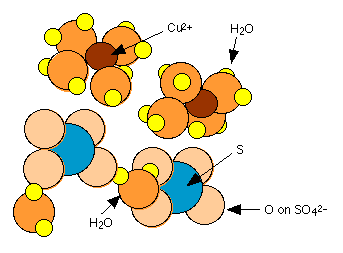
Many common inorganic salts form solids which incorporate water molecules into their crystal structures. These water molecules are usually held rather loosely and can escape as water vapor. Copper(II) sulfate, for example forms a pentahydrate in which four of the water molecules are coordinated to the Cu²⁺ ion while the fifth is hydrogen-bonded to SO₄^2–. This latter water is more tightly bound, so that the pentahydrate loses water in two stages on heating:

\[\ce{CuSO4 \cdot 5H2O ->[140^oC] CuSO4 \cdot 5H2O ->[400^oC] CuSO4} \nonumber\]

These dehydration steps are carried out at the temperatures indicated above, but at any temperature, some moisture can escape from a hydrate. For the complete dehydration of the pentahydrate we can define an equilibrium constant:

\[\ce{CuSO4 \cdot 5H2O(s) <=> CuSO4(s) + 5 H2O(g)} \quad K_p = 1.14 \times 10^{10} \nonumber\]

The vapor pressure of the hydrate (for this reaction) is the partial pressure of water vapor at which the two solids can coexist indefinitely; its value is \(K_p\)^1/5 atm. If a hydrate is exposed to air in which the partial pressure of water vapor is less than its vapor pressure, the reaction will proceed to the right and the hydrate will lose moisture. Vapor pressures always increase with temperature, so any of these compounds can be dehydrated by heating.

Loss of water usually causes a breakdown in the structure of the crystal; this is commonly seen with sodium sulfate, whose vapor pressure is sufficiently large that it can exceed the partial pressure of water vapor in the air when the relative humidity is low. What one sees is that the well-formed crystals of the decahydrate undergo deterioration into a powdery form, a phenomenon known as efflorescence.

Table \(\PageIndex{3}\):

name	formula	vapor pressure, torr
		25°C	30°C
sodium sulfate decahydrate	Na2SO4·10H2O	19.2	25.3
copper(II) sulfate pentahydrate	CuSO4·5H2O	7.8	12.5
calcium chloride monohydrate	CaCl2·H2O	3.1	5.1
(water)	H2O	23.5	31.6

Example \(\PageIndex{4}\)

At what relative humidity will copper sulfate pentahydrate lose its waters of hydration when the air temperature is 30°C? What is \(K_p\) for this process at this temperature?

Solution

From the Table \(\PageIndex{3}\), we see that the vapor pressure of the hydrate is 12.5 torr, which corresponds to a relative humidity of 12.5/31.6 = 0.40 or 40%. This is the humidity that will be maintained if the hydrate is placed in a closed container of dry air

For this hydrate, \(K_p = \sqrt{p_{H_2O)}}\), so the partial pressure of water vapor that will be in equilibrium with the hydrate and the dehydrated solid (remember that both solids must be present to have equilibrium!), expressed in atmospheres, will be

\[\left(\dfrac{12.5}{760}\right)^5 = 1.20 \times 10^{-9}. \nonumber\]

One of the first hydrates investigated in detail was calcium sulfate hemihydrate (CaSO₄·½ H₂O) which Le Chatelier (he of the “principle”) showed to be the hardened form of CaSO₄ known as plaster of Paris. Anhydrous CaSO₄ forms compact, powdery crystals, whereas the elongated crystals of the hemihydrate bind themselves into a cement-like mass that makes this material useful for making art objects, casts for immobilizing damaged limbs, and as a construction material (fireproofing, drywall).