6.3: Dalton's Law

Learning Objectives

Make sure you thoroughly understand the following essential ideas which have been presented below.

• One mole of a gas occupies a volume of 22.4 L at STP (standard temperature and pressure, 273K, 1 atm = 101.3 kPa.)
• The above fact allows us to relate the measurable property of the density of a gas to its molar mass.
• The composition of a mixture of gases is commonly expressed in terms mole fractions; be sure you know how to calculate them.
• Dalton's Law of partial pressures says that every gas in a mixture acts independently, so the total pressure a gas exerts against the walls of a container is just the sum of the partial pressures of the individual components.

Although all gases closely follow the ideal gas law PV = nRT under appropriate conditions, each gas is also a unique chemical substance consisting of molecular units that have definite masses. In this lesson we will see how these molecular masses affect the properties of gases that conform to the ideal gas law. Following this, we will look at gases that contain more than one kind of molecule— in other words, mixtures of gases. We begin with a review of molar volume and the E.V.E.N. principle, which is central to our understanding of gas mixtures.

The Molar Volume of a Gas

You will recall that the molar mass of a pure substance is the mass of 6.02 x 10²³ (Avogadro's number) of particles or molecular units of that substance. Molar masses are commonly expressed in units of grams per mole (g mol^–1) and are often referred to as molecular weights. As was explained in the preceding lesson, equal volumes of gases, measured at the same temperature and pressure, contain equal numbers of molecules (this is the "EVEN" principle, more formally known as Avogadro's law.) Standard temperature and pressure: 273K, 1 atm

The magnitude of this volume will of course depend on the temperature and pressure, so as a means of convenient comparison it is customary to define a set of conditions T = 273 K and P = 1 atm as standard temperature and pressure, usually denoted as STP. Substituting these values into the ideal gas equation of state and solving for V yields a volume of 22.414 liters for 1 mole.

Example \(\PageIndex{1}\)

What would the volume of one mole of air be at 20°C on top of Mauna Kea, Hawa'ii (altitude 4.2 km) where the air pressure is approximately 60 kPa?

Scoria and cinder cones on Mauna Kea's summit in winter. (Public Domain; USGS)

Solution

Apply Boyle's and Charles' laws as successive correction factors to the standard sea-level pressure of 101.3 kPa:

The standard molar volume 22.4 L mol^–1 is a value worth memorizing, but remember that it is valid only at STP. The molar volume at other temperatures and pressures can easily be found by simple proportion. The molar volume of a substance can tell us something about how much space each molecule occupies, as the following example shows.

Example \(\PageIndex{2}\)

Estimate the average distance between the molecules in a gas at 1 atm pressure and 0°C.

Solution

Consider a 1-cm³ volume of the gas, which will contain

\[\dfrac{6.02 \times 10^{23} \;mol^{–1}}{22,400\; cm^3 \;mol^{–1}} = 2.69 \times 10^{19} cm^{-3} \nonumber\]

The volume per molecule (not the same as the volume of a molecule, which for an ideal gas is zero!) is just the reciprocal of this, or \(3.72 \times 10^{-20}\, cm^3\). Assume that the molecules are evenly distributed so that each occupies an imaginary box having this volume. The average distance between the centers of the molecules will be defined by the length of this box, which is the cube root of the volume per molecule:

\[(3.72 \times 10^{–20})^{1/3} = 3.38 \times 10^{–7}\, cm = 3.4\, nm \nonumber\]

Under conditions at which the ideal gas model is applicable (that is, almost always unless you are a chemical engineer dealing with high pressures), "a molecule is a molecule", so the volume of Avogadro's number of molecules will be independent of the composition of the gas. The reason, of course, is that the volume of the gas is mostly empty space; the volumes of the molecules themselves are negligible.

Molar Mass and Density of a Gas

The molecular weight (molar mass) of any gas is the mass, expressed in grams, of Avogadro's number of its molecules. This is true regardless of whether the gas is composed of one molecular species or is a mixture. For a mixture of gases, the molar mass will depend on the molar masses of its components, and on the fractional abundance of each kind of molecule in the mixture. The term "average molecular weight" is often used to describe the molar mass of a gas mixture.

The average molar mass (\(\bar{m}\)) of a mixture of gases is just the sum of the mole fractions of each gas, multiplied by the molar mass of that substance:

\[\bar{m}=\sum_i \chi_im_i\]

Example \(\PageIndex{3}\)

Find the average molar mass of dry air whose volume-composition is O₂ (21%), N₂ (78%) and Ar (1%).

Solution

The average molecular weight is the mole-fraction-weighted sum of the molecular weights of its components. The mole fractions, of course, are the same as the volume-fractions (E.V.E.N. principle.)

\[m = (0.21 \times 32) + (0.78 \times 28) + (0.01 \times 20) = 28 \nonumber\]

The molar volumes of all gases are the same when measured at the same temperature and pressure. However, the molar masses of different gases will vary. This means that different gases will have different densities (different masses per unit volume). If we know the molecular weight of a gas, we can calculate its density.

Example \(\PageIndex{4}\)

Uranium hexafluoride UF₆ gas is used in the isotopic enrichment of natural uranium. Calculate its density at STP.

Solution

The molecular weight of UF₆ is 352.

\[\dfrac{352\; g \;mol^{–1}}{22.4\, L\, mol^{–1}} = 15.7\; g\; L^{–1} \nonumber\]

Note: there is no need to look up a "formula" for this calculation; simply combine the molar mass and molar volume in such a way as to make the units come out correctly.

More importantly, if we can measure the density of an unknown gas, we have a convenient means of estimating its molecular weight. This is one of many important examples of how a macroscopic measurement (one made on bulk matter) can yield microscopic information (that is, about molecular-scale objects.)

Gas densities are now measured in industry by electro-mechanical devices such as vibrating reeds which can provide continuous, on-line records at specific locations, as within pipelines. Determination of the molecular weight of a gas from its density is known as the Dumas method, after the French chemist Jean Dumas (1800-1840) who developed it. One simply measures the weight of a known volume of gas and converts this volume to its STP equivalent, using Boyle's and Charles' laws. The weight of the gas divided by its STP volume yields the density of the gas, and the density multiplied by 22.4 mol^–1 gives the molecular weight. Pay careful attention to the examples of gas density calculations shown here and in your textbook. You will be expected to carry out calculations of this kind, converting between molecular weight and gas density.

Example \(\PageIndex{5}\)

Calculate the approximate molar mass of a gas whose measured density is 3.33 g/L at 30°C and 780 torr.

Solution

Find the volume that would be occupied by 1 L of the gas at STP; note that correcting to 273 K will reduce the volume, while correcting to 1 atm (760 torr) will increase it:

\[V=(1.00 \mathrm{L})\left(\frac{273}{303}\right)\left(\frac{780}{760}\right)=0.924 \mathrm{L} \nonumber\]

The number of moles of gas is

\[n = \dfrac{0.924\, L}{22.4\, L\, mol^{–1}}= 0.0412\, mol \nonumber\]

The molecular weight is therefore

\[\dfrac{33\, g\, L^{–1}}{0.0412\, mol\, L^{–1}} = 80.7\, g\, mol^{–1} \nonumber\]

Density of a Gas Mixture

Gas density measurements can be a useful means of estimating the composition of a mixture of two different gases; this is widely done in industrial chemistry operations in which the compositions of gas streams must be monitored continuously.

Example \(\PageIndex{6}\): Carbon Dioxide and Methane

Find the composition of a mixture of \(\ce{CO2}\) (44 g/mol) and methane \(\ce{CH4}\) (16 g/mol) that has a STP density of 1.214 g/L.

Solution

The density of a mixture of these two gases will be directly proportional to its composition, varying between that of pure methane and pure CO₂. We begin by finding these two densities:

For CO₂:

(44 g/mol) ÷ (22.4 L/mol) = 1.964 g/L

For CH₄:

(16 g/mol) ÷ (22.4 L/mol) = 0.714 g/L

If x is the mole fraction of CO₂ and (1–x) is the mole fraction of CH₄, we can write

1.964 x + 0.714 (1–x) = 1.214

(Does this make sense? Notice that if x = 0, the density would be that of pure CH₄, while if it were 1, it would be that of pure CO₂.)

Expanding the above equation and solving for x yields the mole fractions of 0.40 for CO₂ and 0.60 for CH₄.

Expressing the Composition of a Gas Mixture

Because most of the volume occupied by a gas consists of empty space, there is nothing to prevent two or more kinds of gases from occupying the same volume. Homogeneous mixtures of this kind are generally known as solutions, but it is customary to refer to them simply as gaseous mixtures. We can specify the composition of gaseous mixtures in many different ways, but the most common ones are by volumes and by mole fractions.

Volume Fractions

From Avogadro's Law we know that "equal volumes contains equal numbers of molecules". This means that the volumes of gases, unlike those of solids and liquids, are additive. So if a partitioned container has two volumes of gas A in one section and one mole of gas B in the other (both at the same temperature and pressure), and we remove the partition, the volume remains unchanged.

We can specify the composition of this mixture by saying that the volume fraction of A is 1/3 and that of B is 2/3.

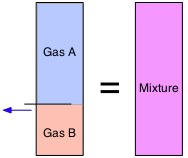
Volume fractions are often called partial volumes:

\[V_i = \dfrac{v_i}{\sum v_i}\]

Don't let this type of notation put you off! The summation sign Σ (Greek Sigma) simply means to add up the v's (volumes) of every gas. Thus if Gas A is the "i-th" substance as in the expression immediately above, the summation runs from i=1 through i=2. Note that we can employ partial volumes to specify the composition of a mixture even if it had never actually been made by combining the pure gases.

When we say that air, for example, is 21 percent oxygen and 78 percent nitrogen by volume, this is the same as saying that these same percentages of the molecules in air consist of O₂ and N₂. Similarly, in 1.0 mole of air, there is 0.21 mol of O₂ and 0.78 mol of N₂ (the other 0.1 mole consists of various trace gases, but is mostly neon.) Note that you could never assume a similar equivalence with mixtures of liquids or solids, to which the E.V.E.N. principle does not apply.

Mole Fractions

These last two numbers (0.21 and 0.78) also express the mole fractions of oxygen and nitrogen in air. Mole fraction means exactly what it says: the fraction of the molecules that consist of a specific substance. This is expressed algebraically by

\[X_i = \dfrac{n_i}{\sum_i n_i}\]

so in the case of oxygen in the air, its mole fraction is

\[ X_{O_2} = \dfrac{n_{O_2}}{n_{O_2}+n_{N_2}+n_{Ar}}= \dfrac{0.21}{1}=0.21 \nonumber\]

Example \(\PageIndex{7}\)

A mixture of \(O_2\) and nitrous oxide, \(N_2O\), is sometimes used as a mild anesthetic in dental surgery. A certain mixture of these gases has a density of 1.482 g L^–1 at 25 and 0.980 atm. What was the mole-percent of \(N_2O\) in this mixture?

Solution

First, find the density the gas would have at STP:

\[\left(1.482 \mathrm{g} \mathrm{L}^{-1}\right) \times\left(\frac{298}{273}\right)\left(\frac{1}{0.980}\right)=1.65 \mathrm{g} \mathrm{L}^{-1}\nonumber \]

The molar mass of the mixture is (1.65 g L^–1)(22.4 L mol^–1) = 37.0 g mol^–1. The molecular weights of \(O_2\) and \(N_2\) are 32 and 44, respectively. 37.0 is 5/12 of the difference between the molar masses of the two pure gases. Since the density of a gas mixture is directly proportional to its average molar mass, the mole fraction of the heavier gas in the mixture is also 5/12:

\[\dfrac{37-32}{44-32}=\dfrac{5}{12}=0.42 \nonumber\]

Example \(\PageIndex{8}\)

What is the mole fraction of carbon dioxide in a mixture consisting of equal masses of CO₂ (MW=44) and neon (MW=20.2)?

Solution

Assume any arbitrary mass, such as 100 g, find the equivalent numbers of moles of each gas, and then substitute into the definition of mole fraction:

• n_CO2 = (100 g) ÷ (44 g mol^–1) = 2.3 mol
• n_Ne= (100 g) ÷ (20.2 g mol^–1) = 4.9 mol
• X_Ne = (2.3 mol) ÷ (2.3 mol + 4.9 mol) = 0.32

Dalton's Law of Partial Pressures

The ideal gas equation of state applies to mixtures just as to pure gases. It was in fact with a gas mixture, ordinary air, that Boyle, Gay-Lussac and Charles did their early experiments. The only new concept we need in order to deal with gas mixtures is the partial pressure, a concept invented by the famous English chemist John Dalton (1766-1844). Dalton reasoned that the low density and high compressibility of gases indicates that they consist mostly of empty space; from this it follows that when two or more different gases occupy the same volume, they behave entirely independently.

The contribution that each component of a gaseous mixture makes to the total pressure of the gas is known as the partial pressure of that gas. Dalton himself stated this law in the simple and vivid way shown at the left.

The usual way of stating Dalton's Law of Partial Pressures is

The total pressure of a gas is the sum of the partial pressures of its components

which is expressed algebraically as

\[P_{total}=P_1+P_2+P_3 ... = \sum_i P_i\]

or, equivalently

\[ P_{total} = \dfrac{RT}{V} \sum_i n_i\]

There is also a similar relationship based on volume fractions, known as Amagat's law of partial volumes. It is exactly analogous to Dalton's law, in that it states that the total volume of a mixture is just the sum of the partial volumes of its components. But there are two important differences: Amagat's law holds only for ideal gases which must all be at the same temperature and pressure. Dalton's law has neither of these restrictions. Although Amagat's law seems intuitively obvious, it sometimes proves useful in chemical engineering applications. We will make no use of it in this course.

Example \(\PageIndex{9}\)

Calculate the mass of each component present in a mixture of fluorine (MW and xenon (MW 131.3) contained in a 2.0-L flask. The partial pressure of Xe is 350 torr and the total pressure is 724 torr at 25°C.

Solution

From Dalton's law, the partial pressure of F₂ is (724 – 350) = 374 torr:

The mole fractions are

\[\chi_{Xe} = \dfrac{350}{724} = 0.48 \nonumber\]

and

\[\chi_{F_2} = \dfrac{374}{724} = 0.52 \nonumber\]

The total number of moles of gas is

\[n=\dfrac{P V}{R T}=\frac{(724 / 60)(2)}{(.082)(298)}=0.078 \mathrm{mol}\nonumber\]

The mass of \(Xe\) is

\[(131.3\, g\, mol^{–1}) \times (0.48 \times 0.078\, mol) = 4.9\, g \nonumber\]

Example \(\PageIndex{10}\)

Three flasks having different volumes and containing different gases at various pressures are connected by stopcocks as shown. When the stopcocks are opened,

1. What will be the pressure in the system?
2. Which gas will be most abundant in the mixture?

Assume that the temperature is uniform and that the volume of the connecting tubes is negligible.

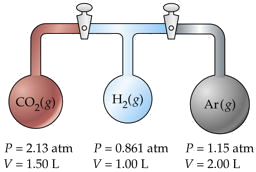
Solution

The trick here is to note that the total number of moles n_T and the temperature remain unchanged, so we can make use of Boyle's law PV = constant. We will work out the details for CO₂ only, denoted by subscripts a.

For CO₂,

P_aV_a = (2.13 atm)(1.50 L) = 3.19 L-atm.

Adding the PV products for each separate container, we obtain

\[\sum P_iV_i = 6.36 L-atm = n_T RT. \nonumber\]

We will call this sum P₁V₁. After the stopcocks have been opened and the gases mix, the new conditions are denoted by P₂V₂.

From Boyle's law,

= 6.36 L-atm. V₂ = ΣV_i = 4.50 L.

Solving for the final pressure P₂ we obtain

(6.36 L-atm)/(4.50 L) = 1.41 atm.

For CO₂, this works out to (3.19/RT) / (6.36/RT) = 0.501. Because this exceeds 0.5, we know that this is the most abundant gas in the final mixture.

Application of Dalton's Law: Collecting Gases over Water

A common laboratory method of collecting the gaseous product of a chemical reaction is to conduct it into an inverted tube or bottle filled with water, the opening of which is immersed in a larger container of water. This arrangement is called a pneumatic trough, and was widely used in the early days of chemistry. As the gas enters the bottle it displaces the water and becomes trapped in the upper part.

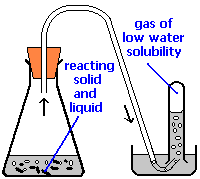
The volume of the gas can be observed by means of a calibrated scale on the bottle, but what about its pressure? The total pressure confining the gas is just that of the atmosphere transmitting its force through the water. (An exact calculation would also have to take into account the height of the water column in the inverted tube.) But liquid water itself is always in equilibrium with its vapor, so the space in the top of the tube is a mixture of two gases: the gas being collected, and gaseous H₂O. The partial pressure of H₂O is known as the vapor pressure of water and it depends on the temperature. In order to determine the quantity of gas we have collected, we must use Dalton's Law to find the partial pressure of that gas.

Example \(\PageIndex{11}\)

Oxygen gas was collected over water as shown above. The atmospheric pressure was 754 torr, the temperature was 22°C, and the volume of the gas was 155 mL. The vapor pressure of water at 22°C is 19.8 torr. Use this information to estimate the number of moles of \(O_2\) produced.

Solution

From Dalton's law, \(P_{O_2} = P_{total} – P_{H_2O} = 754 – 19.8 = 734 \; torr = 0.966\; atm\).

\[n=\frac{P V}{R T}=\frac{0.966 \mathrm{atm} \times(0.155 \mathrm{L})}{\left(.082 \mathrm{L} \mathrm{atm} \mathrm{mol}^{-1} \mathrm{K}^{-1}\right)(295 \mathrm{K})}=.00619 \mathrm{mol}\nonumber\]

Application of Dalton's Law: Scuba diving

Our respiratory systems are designed to maintain the proper oxygen concentration in the blood when the partial pressure of O₂ is 0.21 atm, its normal sea-level value. Below the water surface, the pressure increases by 1 atm for each 10.3 m increase in depth; thus a scuba diver at 10.3 m experiences a total of 2 atm pressure pressing on the body. In order to prevent the lungs from collapsing, the air the diver breathes should also be at about the same pressure.

Figure

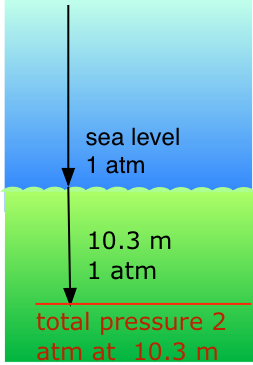
But at a total pressure of 2 atm, the partial pressure of \(O_2\) in ordinary air would be 0.42 atm; at a depth of 100 ft (about 30 m), the \(O_2\) pressure of .8 atm would be far too high for health. For this reason, the air mixture in the pressurized tanks that scuba divers wear must contain a smaller fraction of \(O_2\). This can be achieved most simply by raising the nitrogen content, but high partial pressures of N₂ can also be dangerous, resulting in a condition known as nitrogen narcosis. The preferred diluting agent for sustained deep diving is helium, which has very little tendency to dissolve in the blood even at high pressures.