16.1: Chemistry and Electricity

Learning Objectives

Make sure you thoroughly understand the following essential ideas. It is especially important that you know the precise meanings of all the highlighted terms in the context of this topic.

• Electroneutrality principle - Bulk matter cannot have a chemically-significant unbalance of positive and negative ions.
• Dissolution of a metal in water can proceed to a measurable extent only if some means is provided for removing the excess negative charge that remains. This can be by electron-acceptor ions in solution, or by drawing electrons out of the metal through an external circuit.
• Interfacial potentials - these exist at all phase boundaries. In the case of a metal in contact with an electrolyte solution, the interfacial region consists of an electric double layer.
• The potential difference between a metal and the solution is almost entirely located across the very thin double layer, leading to extremely large potential gradients in this region.

The connection between chemistry and electricity is a very old one, going back to ALESSANDRO VOLTA'S discovery, in 1793, that electricity could be produced by placing two dissimilar metals on opposite sides of a moistened paper.

Electroneutrality

Nature seems to strongly discourage any process that would lead to an excess of positive or negative charge in matter. Suppose, for example, that we immerse a piece of zinc metal in pure water. A small number of zinc atoms go into solution as \(Zn^{2+}\) ions, leaving their electrons behind in the metal:

\[Zn(s) \rightarrow Zn^{2+} + 2e^– \label{1.1.1}\]

As this process goes on, the electrons which remain in the zinc cause a negative charge to build up within the metal which makes it increasingly difficult for additional positive ions to leave the metallic phase. A similar buildup of positive charge in the liquid phase adds to this inhibition. Very soon, therefore, the process comes to a halt, resulting in a solution in which the concentration of \(Zn^{2+}\) is still too low (around 10^–10 M) to be detected by ordinary chemical means.

Figure \(\PageIndex{1}\). Transport of zinc ions from the metal to water; the build-up of negative charge in the metal (and positive charge in the solution) soon brings the process to a halt.

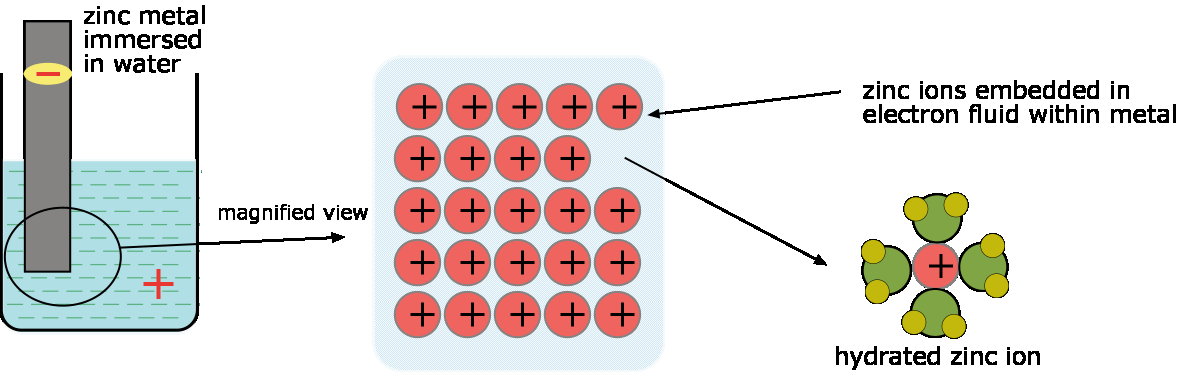
There would be no build-up of this opposing charge in the two phases if the excess electrons could be removed from the metal or the positive ions consumed as the electrode reaction proceeds. For example, we could drain off the electrons left behind in the zinc through an external circuit that forms part of a complete electrochemical cell; this we will describe later. Another way to remove these same electrons is to bring a good electron acceptor (that is, an oxidizing agent) into contact with the electrode. A suitable acceptor would be hydrogen ions; this is why acids attack many metals. For the very active metals such as sodium, water itself is a sufficiently good electron acceptor.

The degree of charge unbalance that is allowed produces differences in electric potential of no more than a few volts, and corresponds to unbalances in the concentrations of oppositely charged particles that are not chemically significant. There is nothing mysterious about this prohibition, known as the electroneutrality principle; it is a simple consequence of the thermodynamic work required to separate opposite charges, or to bring like charges into closer contact. The additional work raises the free energy change of the process, making it less spontaneous.

The only way we can get the oxidation of the metal to continue is to couple it with some other process that restores electroneutrality to the two phases. A simple way to accomplish this would be to immerse the zinc in a solution of copper sulfate instead of pure water. The zinc metal quickly becomes covered with a black coating of finely-divided metallic copper. The reaction is a simple reduction-oxidation reaction involving a transfer of two electrons from the zinc to the copper:

\[ Zn(s) \rightarrow Zn^{2+} + 2e^– \label{1.1.2} \]

and

\[ Cu^{2+} + 2e^– \rightarrow Cu(s) \label{1.1.3}\]

The dissolution of the zinc is no longer inhibited by a buildup of negative charge in the metal, because the excess electrons are removed from the zinc by copper ions that come into contact with it. At the same time, the solution remains electrically neutral, since for each \(Zn\) ion introduced to the solution, one \(Cu\) ion is removed. The net reaction

\[Zn(s) + Cu^{2+} \rightarrow Zn^{2+} + Cu(s) \label{1.1.4}\]

quickly goes to completion.

Potential differences at interfaces

The transition region between two phases consists of a region of charge unbalance known as the electric double layer. As its name implies, this consists of an inner monomolecular layer of adsorbed water molecules and ions, and an outer diffuse region that compensates for any local charge unbalance that gradually merges into the completely random arrangement of the bulk solution. In the case of a metal immersed in pure water, the electron fluid within the metal causes the polar water molecules to adsorb to the surface and orient themselves so as to create two thin planes of positive and negative charge. If the water contains dissolved ions, some of the larger (and more polarizable) anions will loosely bond (chemisorb) to the metal, creating a negative inner layer which is compensated by an excess of cations in the outer layer.

Electrochemistry is the study of reactions in which charged particles (ions or electrons) cross the interface between two phases of matter, typically a metallic phase (the electrode) and a conductive solution, or electrolyte. A process of this kind can always be represented as a chemical reaction and is known generally as an electrode process. Electrode processes (also called electrode reactions) take place within the double layer and produce a slight unbalance in the electric charges of the electrode and the solution. Much of the importance of electrochemistry lies in the ways that these potential differences can be related to the thermodynamics and kinetics of electrode reactions. In particular, manipulation of the interfacial potential difference affords an important way of exerting external control on an electrode reaction.

The interfacial potential differences which develop in electrode-solution systems are limited to only a few volts at most. This may not seem like very much until you consider that this potential difference spans a very small distance. In the case of an electrode immersed in a solution, this distance corresponds to the thin layer of water molecules and ions that attach themselves to the electrode surface, normally only a few atomic diameters. Thus a very small voltage can produce a very large potential gradient. For example, a potential difference of one volt across a typical 10^–8 cm interfacial boundary amounts to a potential gradient of 100 million volts per centimeter— a very significant value indeed!

Interfacial potentials are not confined to metallic electrodes immersed in solutions; they can in fact exist between any two phases in contact, even in the absence of chemical reactions. In many forms of matter, they are the result of adsorption or ordered alignment of molecules caused by non-uniform forces in the interfacial region. Thus colloidal particles in aqueous suspensions selectively adsorb a given kind of ion, positive for some colloids, and negative for others. The resulting net electric charge prevents the particles from coming together and coalescing, which they would otherwise tend to do under the influence of ordinary van der Waals attractions.

Interfacial potential differences are not directly observable. The usual way of measuring a potential difference between two points is to bring the two leads of a voltmeter into contact with them. It's simple enough to touch one lead of the meter to a metallic electrode, but there is no way you can connect the other lead to the solution side of the interfacial region without introducing a second electrode with its own interfacial potential, so you would be measuring the sum of two potential differences. Thus single electrode potentials, as they are commonly known, are not directly observable.

What we can observe, and make much use of, are potential differences between pairs of electrodes in electrochemical cells. This is the topic of the next page in this series.

Summary

Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially important that you know the precise meanings of all the highlighted terms in the context of this topic.

• Electroneutrality principle - Bulk matter cannot have a chemically-significant unbalance of positive and negative ions.
• Dissolution of a metal in water can proceed to a measurable extent only if some means is provided for removing the excess negative charge that remains. This can be by electron-acceptor ions in solution, or by drawing electrons out of the metal through an external circuit.
• Interfacial potentials - these exist at all phase boundaries. In the case of a metal in contact with an electrolyte solution, the interfacial region consists of an electric double layer.
• The potential difference between a metal and the solution is almost entirely located across the very thin double layer, leading to extremely large potential gradients in this region.