6.12: Solutions for Selected Problems

Exercise 6.1.1:

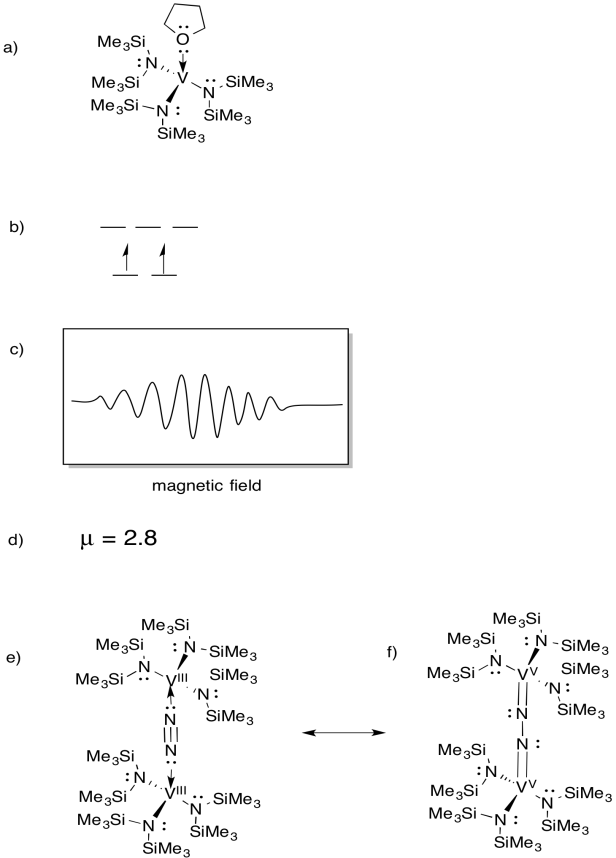
Exercise 6.1.2:

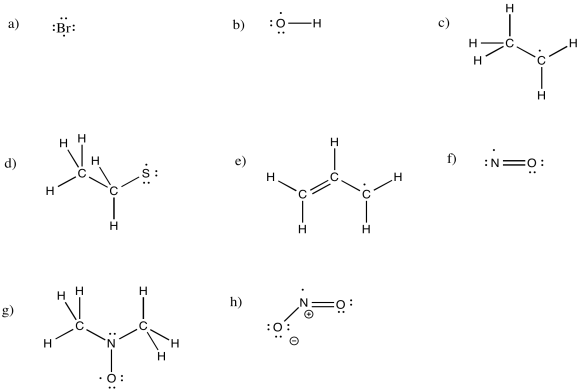
Exercise 6.1.4:

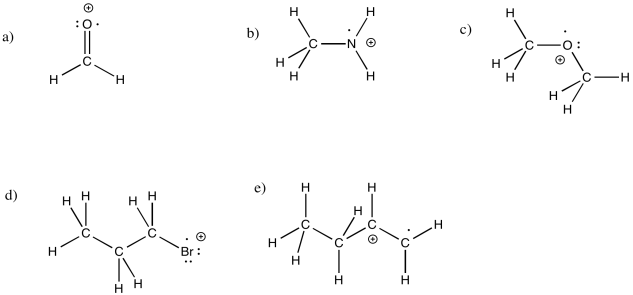
Exercise 6.1.5:

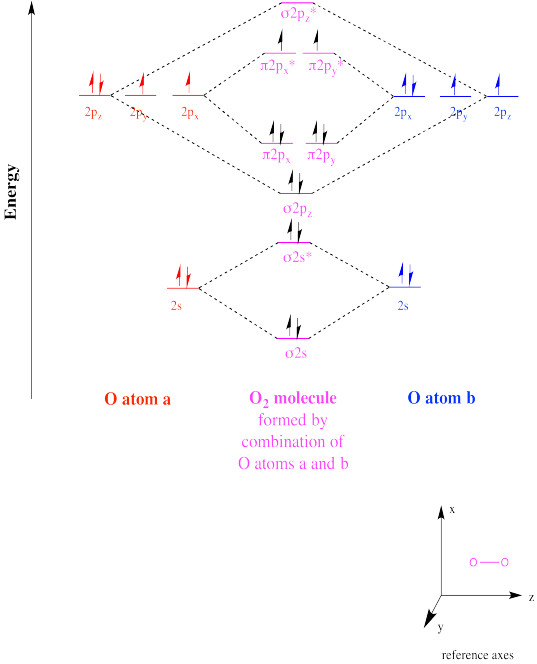
Exercise 6.1.6:

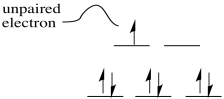
Exercise 6.2.2:

a)

b)

c)

Exercise 6.2.3:

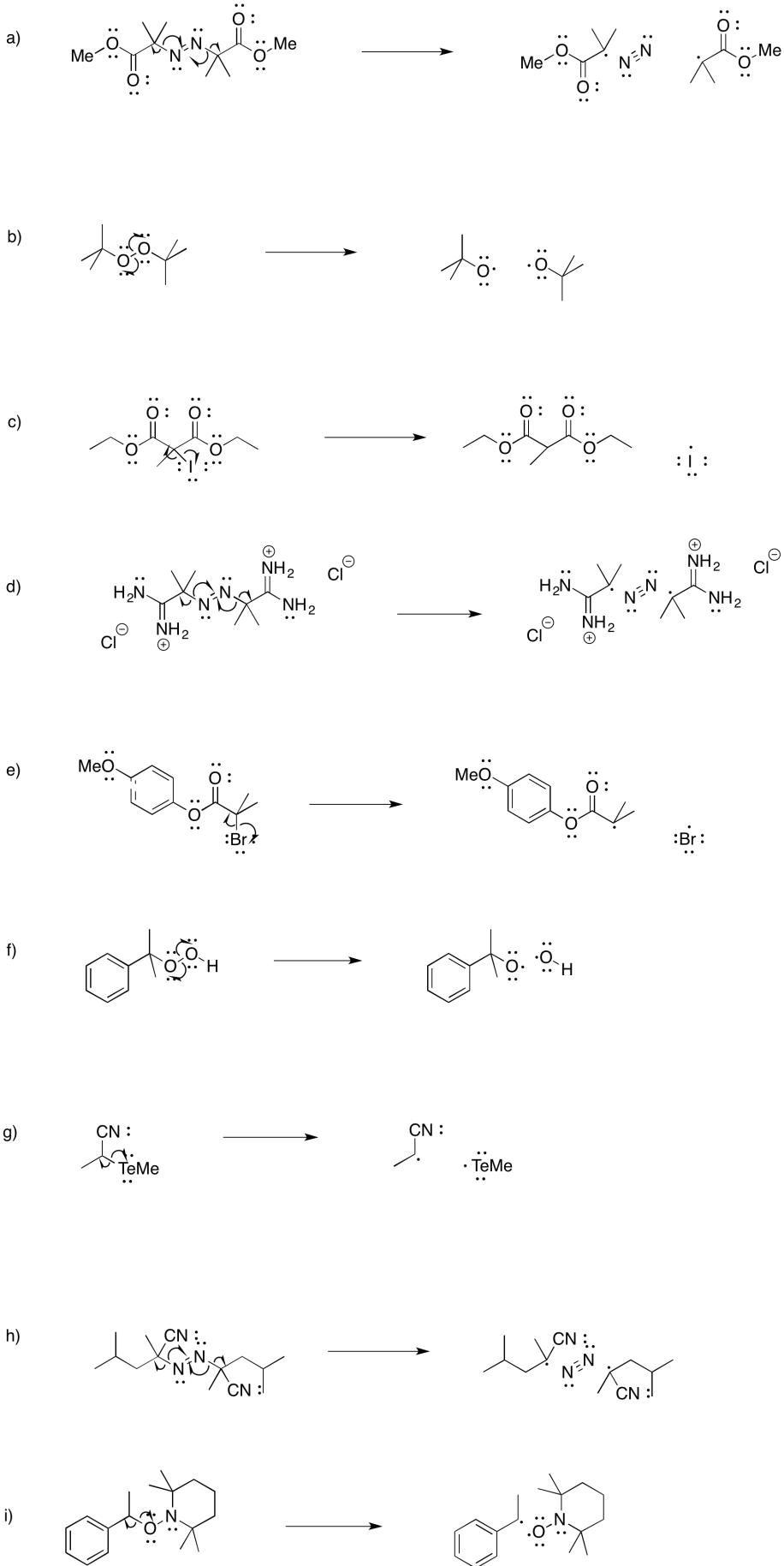
Exercise 6.3.1:

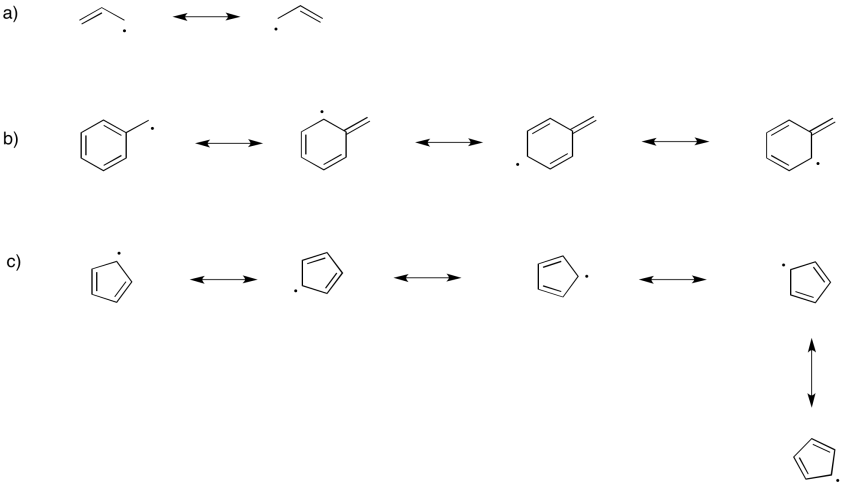
Exercise 6.3.2:

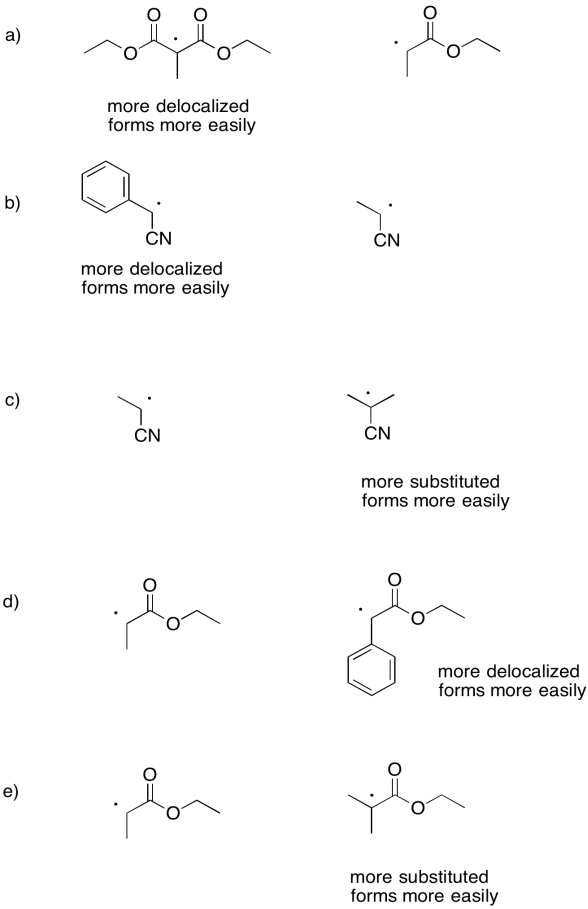
Exercise 6.3.3:

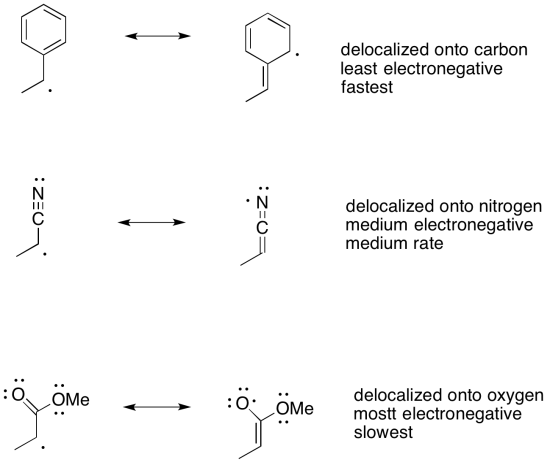
Exercise 6.4.1:

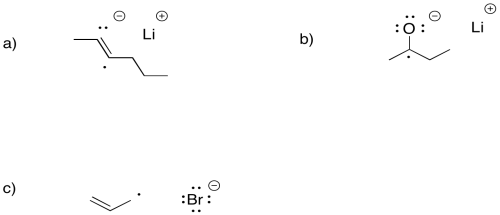
Exercise 6.4.2:

The reduction potential of the negatively charged carboxylate anion would be much less positive than the reduction potential for the neutral aldehyde or ketone. We think of a carboxylate anion as much less electrophilic than aldehydes and ketones for the same reason.

Exercise 6.4.3:

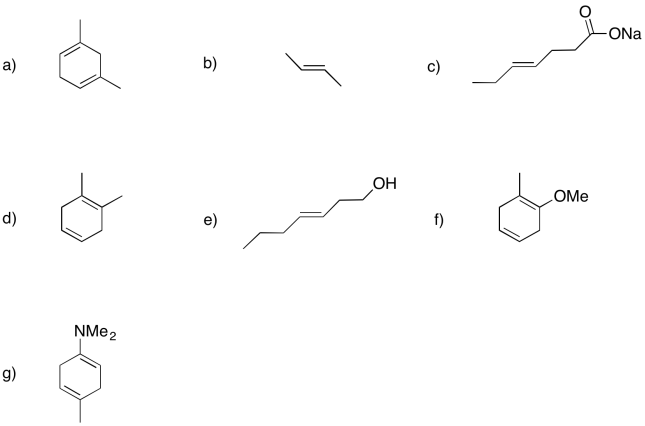
Exercise 6.4.4:

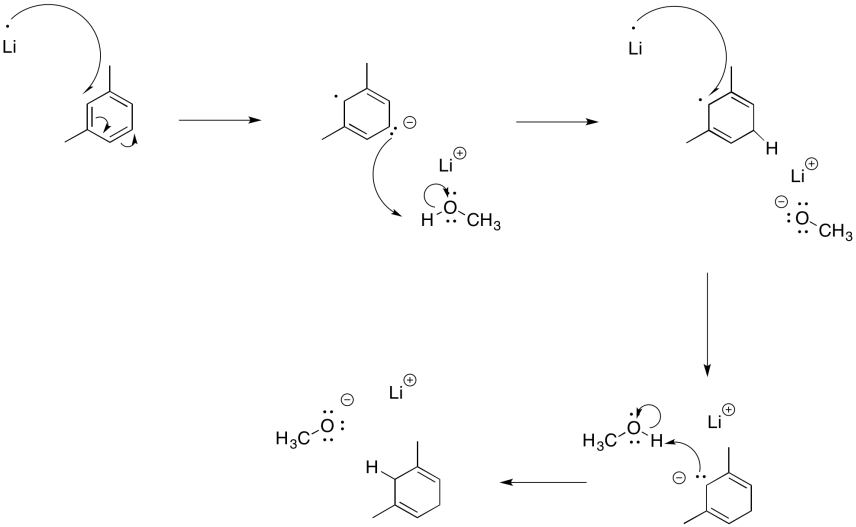
Exercise 6.5.1:

Exercise 6.5.3:

a) no; a stronger bond would have to be broken and replaced with a weaker bond.

b) yes; a weaker bond would be broken and replaced with a stronger one.

c) no

d) yes

e) no

f) yes

Exercise 6.5.4:

a) no b) yes c) no

Exercise 6.5.5:

1. The effect is similar to the stability of carbocations. The more substituted radical is more stable. Thus, the trend from most to least stable is tertiary > secondary > primary > methyl radical. The trend likely originates from a hyperconjugation effect, as in carbocations.
2. The trend here is that if the radical is delocalized by resonance, it is more stable. The allyl and benzyl radicals are more stable than the isopropyl radical. This trend is also seen in cations.
3. The trend here has to do with "hybridization effects" or the atomic orbitals that contribute to the formation of molecular orbitals involved in the relevant bond. In a linear alkyne, the C-H bond can be formed only from some combination involving a hydrogen 1s orbital, carbon 2s orbital and one of the carbon 2p orbitals. This combination is called a "sp" hybrid and the orbital that combines with the hydrogen can be considered 50% 2s, 50% 2p in character.

In a planar alkene, the C-H bond can be formed only from some combination involving a hydrogen 1s orbital, carbon 2s orbital and two of the carbon 2p orbitals (since two of them could lie in this plane). This combination is called a "sp²" hybrid and the orbital that combines with the hydrogen can be considered 33% 2s, 66% 2p in character.

In a tetrahedral alkane, the C-H bond can be formed from some combination involving a hydrogen 1s orbital, carbon 2s orbital and all three of the carbon 2p orbitals. This combination is called a "sp³" hybrid and the orbital that combines with the hydrogen can be considered 25% 2s, 75% 2p in character.

Because a 2s orbital is lower in energy than a 2p orbital, a bond that has greater 2s character is lower in energy than a bond with less 2s character. That means that a bond with greater 2s character is harder to break than a bond with less 2s character. Hence, the alkane C-H bond is weaker than the alkene C-H bond, which is weaker than the alkyne C-H bond.

Exercise 6.5.6:

The Sn-H bond has a dissociation energy of about 78 kcal/mol, compared to about 98 kcal/mol for the C-H bond in ethane. The formation of the Sn-H bond would not compensate for the energy needed to break the C-H bond. On the other hand, the 100 kcal/mol released upon formation of a Sn-Cl bond would more than make up for the 85 kcal/mol required to breal a C-Cl bond.

We could try to rationalise those differences, although bond strengths are always very complicated issues and we will not be able to explain things satisfactorily without quantum mechanical calculations. Let's start with two basic factors, though: the amount of covalency and the amount of polarity.

The difference between the covalent radii of tin and hydrogen (1.39 vs. 0.31 Å) is much greater than the difference between tin and chlorine (1.39 vs 1.02 Å), so there may be less overlap and less covalency between tin and hydrogen than between tin and chlorine. By comparison, the covalent radius of carbon is about 0.76, which puts it somewhere in between hydrogen and chlorine.

In addition, as measured on the Pauling scale, the electronegativity values of these atoms are: chlorine, 3.16; carbon, 2.55; hydrogen, 2.2; tin, 1.96. The tin-chlorine bond would have a large ionic component; this additional component of bonding would strengthen the Sn-Cl bond.

Exercise 6.5.7:

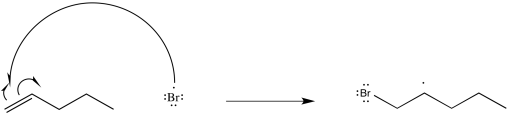
Exercise 6.5.8:

1. 174 - 90 kcal/mol = 84 kcal/mol for the π contribution only
2. 179 - 92 kcal/mol = 87 kcal/mol for the π contribution only

Exercise 6.5.9:

1. 85 + 77 kcal/mol = 162 kcal/mol for the combined σ + π contribution
2. There may be significant differences between the π bond in methanal imine (CH₂=NH) and the imine for which we have bond strength data. For example, breaking the bond would result in radicals next to phenyl groups, which may be significantly stabilized. On the other hand, the π bond itself may be significantly stabilized by conjugation. Thus, our estimate is probably not correct, but it is difficult to say whether it is too high or too low.

Exercise 6.7.1:

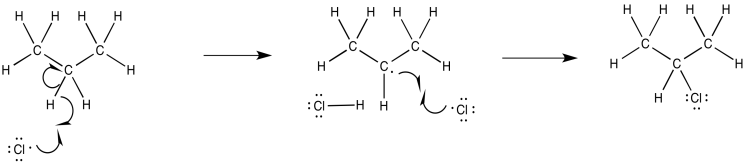
Exercise 6.9.2:

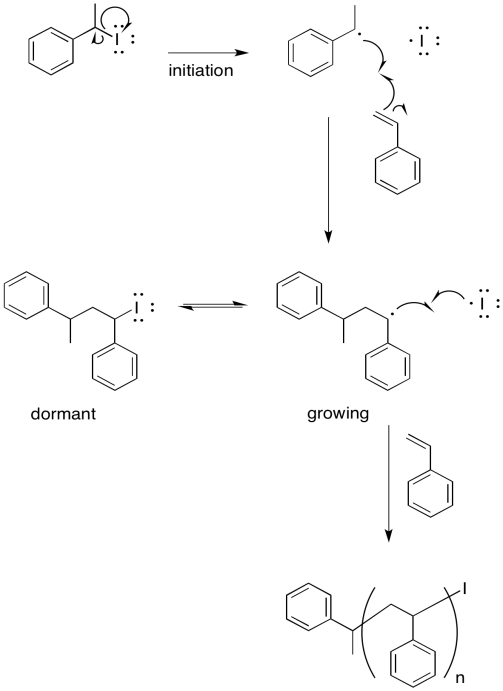
The mechanism would begin with initiation of the benzoyl peroxide.

The resulting phenyl radical acts as the initiator for polymerisation.

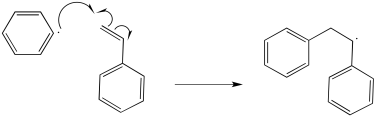
Additional propagation steps follow.

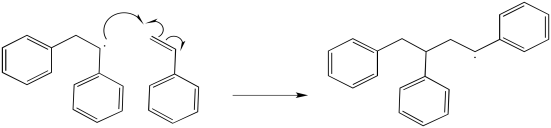
Exercise 6.9.3:

The monomer dependence is straightforward: the more monomer there is present, the faster it can be enchained by the growing radical chain.

The initiator dependence is slightly more complicated, but not much. The more growing radical chains there are, the faster the monomers can be enchained. The more phenyl radical is formed, each initiating a new radical chain, then the more growing radical chains there will be.

\[Rate = k[monomer][Ph \cdot] \nonumber\]

The more benzoyl peroxide there is, the more phenyl radical there will be, but the relationship is not linear, as explained below.

Benzoyl peroxide cleaves in two, ultimately producing two phenyl radicals:

\[K_{eq} = \frac{[Ph \cdot]^{2}}{[BP]} \nonumber\]

so \([Ph \cdot]^{2} = K_{eq}[BP]\)

and \([Ph \cdot] = K_{eq}^{1/2}[BP]^{1/2}\)

therefore \(Rate= k[monomer][Ph \cdot]^{1/2}\)

Exercise 6.9.4:

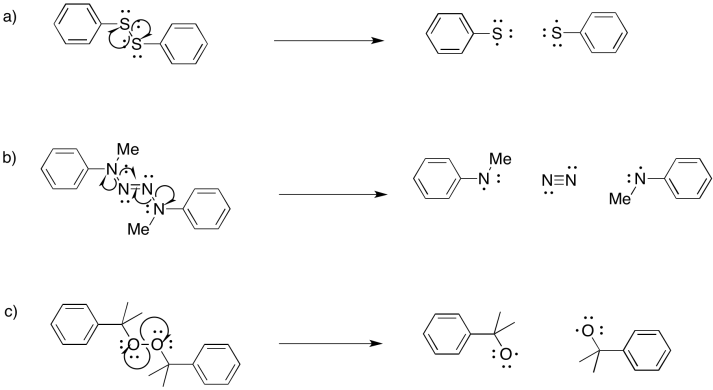
Exercise 6.9.5:

Exercise 6.9.6:

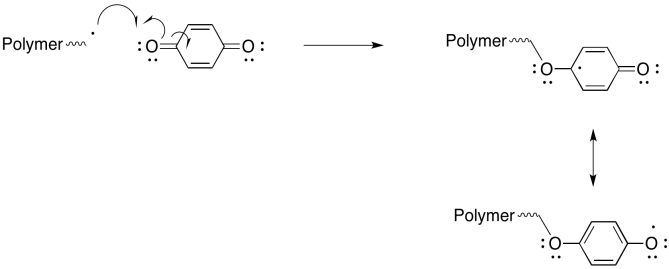
Exercise 6.9.7:

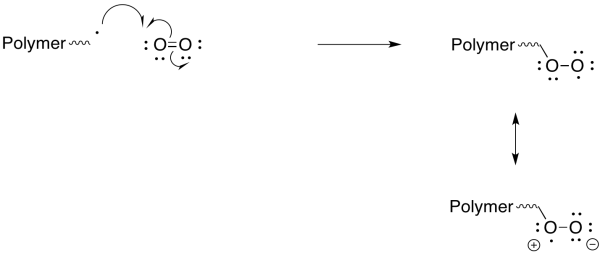
Peroxy radicals are relatively stable and react slowly. However, when they do react, they also undergo reactions other than radical polymerisation, so that they are even more effective as inhibitors of polymerisation.

Exercise 6.10.1:

Because each initiator breaks in half, forming two radicals, one initiator starts two growing chains. Every initiator will, on average, consume half the monomers, assuming no unexpected chain termination events.

1. DP = 500 monomers / 2 growing chains = 250
2. DP = 1000 monomers / 2 growing chains = 500
3. DP = 600 monomers / 3 growing chains = 200

Exercise 6.10.2:

M₀ = molecular weight of monomer in each case. 1 D (Dalton) = 1 amu

a) \(M_{n} = DP \times M_{0} = 1250 \times 104 D = 130000D = 130 kD}\)

b) \(M_{n} = DP \times M_{0} = 725 \times 85 D = 61625D = approximately \: 62 kD}\)

c) \(M_{n} = DP \times M_{0} = 1420 \times 86 D = 122120 D = approximately \: 122 kD}\)

Note that end groups were neglected in these calculations; they may contribute a significant percentage of total molecular weight at lower DP. A more accurate calculation would account for the identity of both end groups.

Exercise 6.10.3:

1. \(DP = \frac{M_{n}}{M_{0}} = \frac{11450D}{53D} = 216}\)
2. (DP = \frac{M_{n}}{M_{0}} = \frac{24760D}{86D} = 288}\)
3. (DP = \frac{M_{n}}{M_{0}} = \frac{927000D}{104D} = 8914}\)

Exercise 6.10.4:

1. \(MW = 8 \times 100D = 800 D\)
2. 15 monomers / 3 chains = 5 new monomers / chain

\[DP = 8 + 5 = 13 \nonumber\]

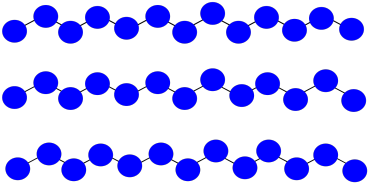
c) \(MW = 13 \times 100 D = 1300 D\)

d) All chains are the same length; PDI = 1.0

e) \(MW = 16 \times 100 D = 1600D\)

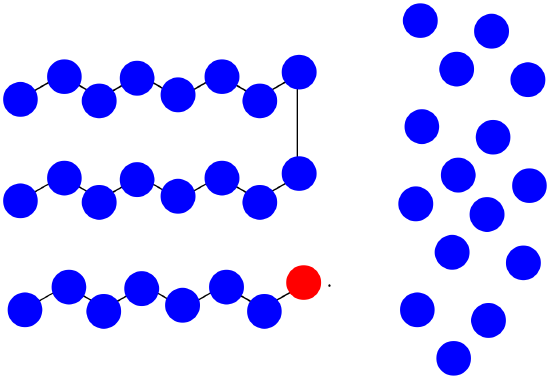
f) \(MW = ( 8 + 15) \times 100D = 2300D\)

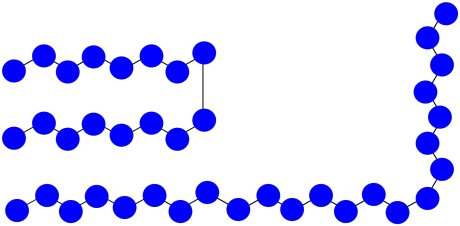
g) \(M_{n} = \frac{2300 + 1600D}{2} = 1950D\)

h) \(PDI = \frac{2300D}{1600D} = 1.44\)

Exercise 6.10.5:

a) The chain that abstracted the hydrogen: \(MW = 8 \times 100D = 800D\)

The branched chain: \(MW = 18 \times 100D = 1800 D\)

The normal chain: \(MW = 13 \times 100D = 1300D \)

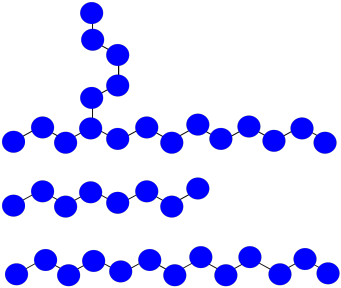
b) \(M_{n} = \frac{1800 + 1300 + 800D}{3} = 1300D\)

c) \(PDI = \frac{1800}{800D} = 2.25\)

Exercise 6.10.6:

1. \(M_{n} = \frac{17000 + 1800 + 300D}{3} = \frac{3800D}{3} = 1267\)
2. \(M_{n} = \frac{1700 + 1800}{2} = \frac{3500D}{2} = 1750D\)

Exercise 6.10.7:

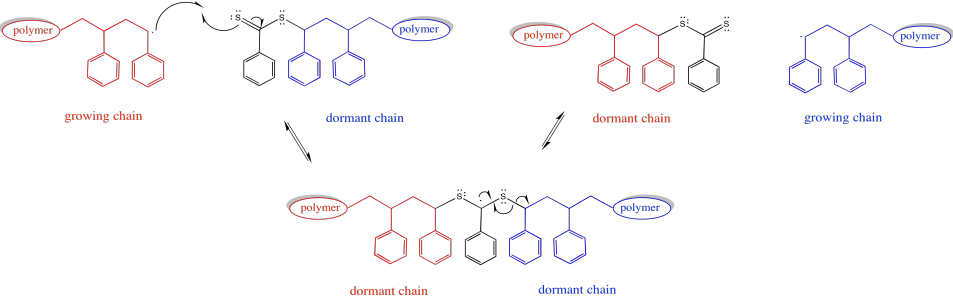
Exercise 6.10.8:

Exercise 6.10.9:

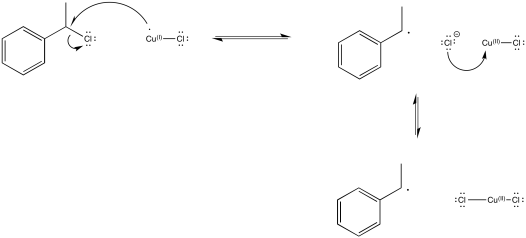
Exercise 6.11.1:

The combinations are:

1. all spins down (and there is only one way to do that)
2. two of the spins are down, but one is up (and each of the three protons could be up, so there are three ways of doing that)
3. two of the spins are up, but one is down (and each of the three protons could be down, so there are three ways of doing that)
4. all spins up (and there is just one way to do that).

The result is a 1:3:3:1 quartet.

Exercise 6.11.2:

a) singlet b) doublet c) triplet d) quartet

Exercise 6.11.3:

A septet (in a 1:3:5:7:5:3:1 ratio).

Exercise 6.11.4:

1. an octet (in a 1:3:5:7:7:5:3:1 ratio)
2. a sextet (in a 1:3:5:5:3:1 ratio)
3. a singlet
4. an octet
5. a quartet (in a 1:3:3:1 ratio)

Exercise 6.11.5: