6.11: Detection of Unpaired Electrons

Last updated
Save as PDF

Page ID: 202843

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

There are experimental methods for the detection of unpaired electrons. One of the hallmarks of unpaired electrons in materials is interaction with a magnetic field. That interaction can be used to provide information about compounds containing unpaired electrons.

Electron Paramagnetic Resonance

Electron paramagnetic resonance (EPR) or electron spin resonance (ESR) is a spectroscopic method. It depends upon the energetic separation of two spin states that exists only in the presence of a magnetic field.

EPR is very closely related to another common type of spin resonance spectroscopy, NMR.

Spin is a quantum property that has no real analogy that would make sense to us on a macroscopic level. However, we do know that spin has associated with it magnetic properties. An electron can have either of two values for these magnetic properties. There are various labels given to these values: sometimes "up" and "down", sometimes, +1/2 and -1/2. However, whichever value of spin an electron possesses makes no difference energetically.

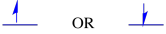
The two possible spin states are the same energetically -- unless a magnetic field is present. Once that situation arises, there is an energetic separation between the two states.

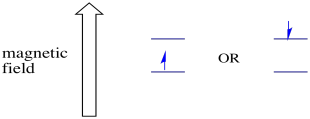
In the presence of a magnetic field, the two spin states separate into two different energy levels. The amount of separation between the energy levels depends on the magnitude of the magnetic field. The stronger the magnetic field, the greater the separation.

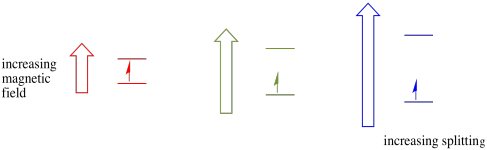
This case is only true for unpaired spins. Remember, unpaired spins interact with a magnetic field. If everything is spin-paired, nothing happens. That's very useful, because it gives us a way to detect those unpaired electrons.

An electron in one spin state can still be excited to the other by the absorbance of a photon. Alternatively, an electron in the higher state can drop down to the lower one if it releases a photon.

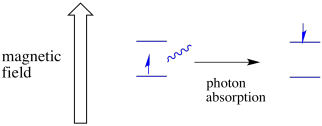
In order for any of this to happen, the energy of the photon must exactly match the energy difference between states. This Goldilocks rule is called the resonance condition. The amount of energy supplied to jump from one energy level to the next has to be just right. Too little energy and the electron won't make it. Too much energy and the electron won't make it either. It's waiting for just the right photon.

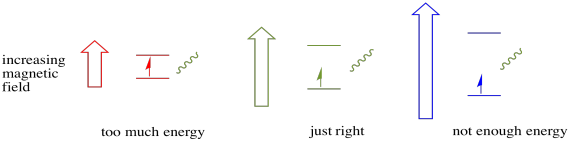
Just how much energy does a photon have? Remember your Planck-Einstein relationship. It described the energy of a photon:

\[E=h \nu \nonumber\]

E is the energy of the photon, h is Planck's constant (6.625 x 10^-34 Js) and ν is the frequency of the photon (it looks like a Roman vee, but it's the Greek letter, nu).

Alternatively, because of the relationship between wavelength and frequency:

\[E= \frac{hc}{\lambda} \nonumber\]

The new quantities are c, the speed of light (3.0 x 10⁸ m s^-1) and λ, the wavelength of the photon.

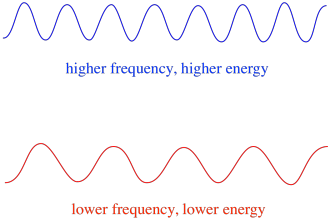
So, in general, different wavelengths of light deliver different amounts of energy. Blue light, with a wavelength close to 475 nm, has more energy than red light, with a wavelength close to 700 nm.

In EPR, the general range of electromagnetic radiation, or the general kind of photon, is microwave radiation. The frequency of these photons is about 9 or 10 GHz. (Another type of spectroscopy, rotational spectroscopy, also measures the absorbance of microwaves. It typically uses somewhat higher frequencies of microwaves. Rotational spectroscopy gives structural or bonding information about molecules in the gas phase.)

Depending on the environment of the unpaired electron, it may be more susceptible or less susceptible to the influence of the external magnetic field. That means the energy splitting between the two spin states will vary from one molecule to another. As a result, different molecules in the same magnetic field would absorb different wavelengths of microwave radiation.

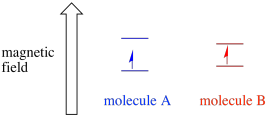
Usually, an EPR spectrometer is designed so that it supplies a fixed wavelength of microwave radiation to the sample. The magnetic field is adjusted and the instrument measures what field strength was required for absorption of the photons. An EPR spectrum shows absorbance as a function of magnetic field strength.

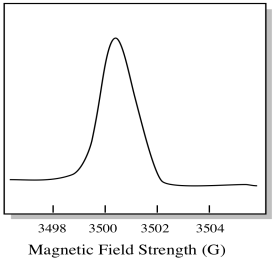
There is something a little different about how EPR spectra are usually displayed. It is displayed as a derivative of the plot shown above. That's because of the way that the instrument measures the change in absorbance as it changes the magnetic field; i.e. it measures d(absorbance)/d(magnetic field). That's the slope of the previous plot.

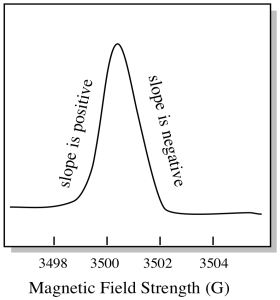
As a result, an EPR spectrum really looks more like this. The part above the baseline reflects the positive slope in the previous plot. The part below the baseline reflects the negative slope in the previous plot.

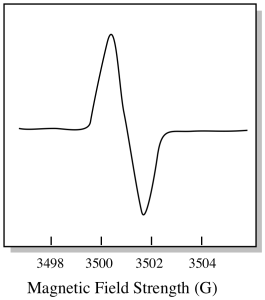
The magnetic field strength is not typically the value that is reported for the peak position. Instead, something called the g-value is reported. The g-value arises from the equation for the Zeeman effect (the effect of the magnetic field on the splitting between spin energy levels). That relationship is:

\[\Delta E = g \beta B \nonumber\]

in which ΔE is the energy difference between spin states, g is the g-value, a proportionality constant that depends on how susceptible the electron is to the influence of the magnetic field, β is the Bohr magneton (9.274 x 10^-24 J T^-1) and B is the applied magnetic field.

That means that, for photon absorption,

\[h \nu = g \beta B \nonumber\]

and so

\[g = \frac{ h \nu}{\beta B} \nonumber\]

Remember, h and β are just constants. That means g is a measure of the ratio of the photon absorbed to the magnetic field used. It's a standardisation step. If people have instruments that use slightly different wavelengths of microwave radiation, then the magnetic fields they measure for the same samples would not agree. If everyone just measures the ratio of wavelength to field strength, it should all even out. The g-value is a reproducible measure of the environment of an electron that should be the same from one laboratory to another.

A similar practice is used in NMR spectroscopy, for similar reasons. When we report a chemical shift in ppm instead of Hz, we are correcting for the strength of the magnetic field in the instrument we are using. Otherwise the same sample would give two different shifts on two different instruments.

Coupling in EPR

Coupling is a phenomenon in which magnetic fields interact with each other. In EPR, coupling comes about because of the influence of nearby nuclei on the electron that is being observed.

For example, you may already know that a hydrogen atom's nucleus has an unpaired spin. That's the basis of ¹H NMR spectroscopy. If that nucleus has an unpaired spin, it has an associated magnetic field. Because the hydrogen nucleus could have either spin value, +1/2 or -1/2, then it has two possible magnetic fields associated with it.

A nearby electron, placed in an external magnetic field, could now be in either of two different situations. Either the neighbouring proton adds a little bit to the magnetic field, or it subtracts a little bit from the external field.

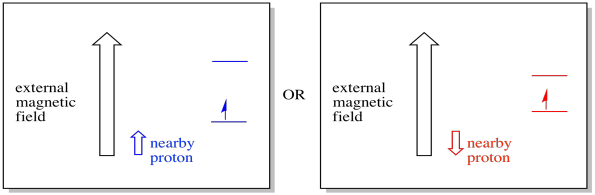
As a result, the electron can experience two different fields. Remember, we are not dealing with a single molecule in spectroscopy. We are dealing with huge numbers of molecules. Some of the molecules will be in one situation. Some of the molecules will be in the other situation. We will see both situations. There will be absorbance at two different magnetic field strengths.

As a result, the EPR spectrum shows two peaks, like this:

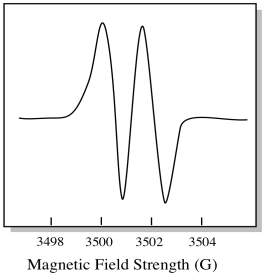
This type of peak in the spectrum is called a doublet, because of the double absorbance. This characteristic of an EPR peak is called its multiplicity. How many lines is the peak split into? Two. It is a doublet.

Things are even more interesting if there are two nearby protons. In that case, both neighbouring protons have spin. Either spin could have value +1/2 or -1/2. Maybe they are both +1/2. Maybe they are both -1/2. Maybe there is one of each. These three possible combinations will have three different effects on the magnetic field experienced by the electron.

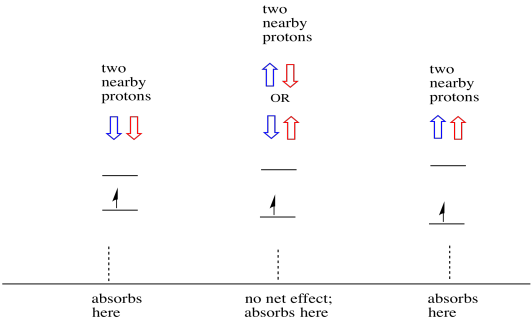
As a result, there are three peaks in the spectrum. The spectrum is called a triplet. This triplet is shown below, underneath the diagram that illustrates the spin combinations of the neighbouring hydrogens.

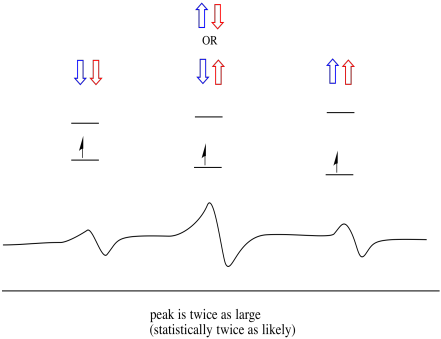
Notice that, because either hydrogen could be up or down in the mixed combination, there are two ways of arriving at that middle state. That combination is twice as likely as the other two, because there is only one way of getting those combination: both hydrogens' spins are up, in one case. Both hydrogens are down in the other. As a result, the middle peak in a triplet is twice as large as the peaks on the edges.

Exercise \(\PageIndex{1}\)

Show that, with three neighbouring hydrogens, a quartet would result, in which the ratios of the peaks are 1:3:3:1.

Answer

The combinations are:

a) all spins down (and there is only one way to do that)

b) two of the spins are down, but one is up (and each of the three protons could be up, so there are three ways of doing that)

c) two of the spins are up, but one is down (and each of the three protons could be down, so there are three ways of doing that)

d) all spins up (and there is just one way to do that).

The result is a 1:3:3:1 quartet.

Exercise \(\PageIndex{2}\)

Predict the multiplicity in the EPR spectrum for each of the following alkoxy radicals (note that oxygen and carbon have no unpaired spins; assume the same is true for X):

a) X₃C-O^. b) X₂CH-O^. c) XCH₂-O^. d) CH₃-O^.

Answer a: a) singlet
Answer b: b) doublet
Answer c: c) triplet
Answer d: d) quartet

Exercise \(\PageIndex{3}\)

Suppose benzene were reduced by one electron to obtain the benzene radical anion. What would be the multiplicity in the EPR spectrum?

Answer: A septet (in a 1:3:5:7:5:3:1 ratio).

Coupling to Metal Ions

Lots of nuclei other than hydrogen have a net spin. If the unpaired electron happens to be found on a metal, the EPR spectrum may provide confirmation of that structural information. This confirmation may come from both the magnetic field information (similar to chemical shift in NMR) and from the multiplicity.

Nuclear spins of selected metals are shown below.

Metal	Spin
V	7/2
Mn	5/2
Fe	0
Co	7/2
Cu	3/2

In each of these metals, the nucleus has different possible magnetic fields. Note that their effects are slightly more complicated than that of a hydrogen atom. For example, copper, with spin 3/2, acts a little like three different hydrogen nuclei (each with spin +/- 1/2) in terms of its effect on a nearby electrom's EPR spectrum. The multiplicity of an unpaired electron on a copper ion should be pretty distinctive.

Exercise \(\PageIndex{4}\)

Predict the multiplicity of a peak in the EPR spectrum for an unpaired electron on each of the following metals:

a) vanadium b) manganese c) iron d) cobalt e) copper

Answer a: a) an octet (in a 1:3:5:7:7:5:3:1 ratio)
Answer b: b) a sextet (in a 1:3:5:5:3:1 ratio)
Answer c: c) a singlet
Answer d: d) an octet
Answer e: e) a quartet (in a 1:3:3:1 ratio)

Sometimes things are more complicated, because different isotopes of the same element may have different possible spin values. In fact, that is true with hydrogen and carbon, but the great majority of hydrogen is found as ¹H, so in general we can think of it as having spin = 1/2; the great majority of carbon is ¹²C, with spin = 0.

The natural isotopes of iron, and their nuclear spins, are shown in the table below.

Isotope	Spin	% Abundance
⁵⁴Fe	0	5.9
⁵⁶Fe	0	91.8
⁵⁷Fe	1/2	2.1
⁵⁸Fe	0	0.2

The EPR spectrum of an unpaired electron on iron may be slightly more complicated than we first thought. Within the sample, some of the electrons would be situated on iron ions with spin = 1/2, although most would not. This complication may be enough to introduce a slight variation in the appearance of the spectrum, but overall it would still look pretty much like a singlet.

However, in many cases things do get much more complex. Molybdenum provides a good example.

Isotope	Spin	% Abundance
⁹²Mo	0	14.8
⁹⁴Mo	0	9.3
⁹⁵Mo	5/2	15.9
⁹⁶Mo	0	16.7
⁹⁷Mo	5/2	9.6
⁹⁸Mo	0	24.1
¹⁰⁰Mo	0	9.6

There are seven naturally occurring isotopes of molybdenum. Five of them have spin = 0, so an unpaired electron on those isotopes would give rise to a simple singlet in the EPR spectrum. The other two isotopes, comprising 25% of the total, have spin = 5/2. Most unpaired electrons on molybdenum would show up as a singlet. However, a significant fraction would show up as a sextet. That means that, in an ideal case, an unpaired electron on molybdenum would give rise to a singlet with a sextet superimposed on it (about a quarter as strong as the singlet).

This situation might look something like the drawing below.

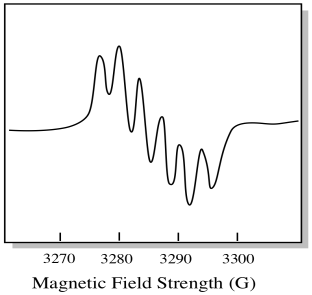
In reality, EPR spectra are enormously complicated in many cases. They often look like fuzzy blobs. There are so many things coupling to so many other things that it becomes almost impossible to decipher by eye. In most cases, computer simulations are run and the experimental data is compared to the computer simulations to obtain structural insight.

Exercise \(\PageIndex{5}\)

Vanadium is present in some nitrogenases and so there has been interest in model complexes (e.g. Sandro Gambarotta et al, J. Am. Chem. Soc. 1994, 116, 6927-6928). Gambarotta used the following synthesis, in THF solvent:

\[\ce{VCl3 + [(Me3Si)2N]K -> [(Me3Si)2N]3V (THF)} \nonumber\]

Draw the structure of the product of the reaction.
Draw a d orbital splitting diagram for this complex.
An EPR spectrum was recorded for this compound. Sketch the spectrum, given that vanadium has nuclear spin I = 7/2.
Estimate μ_eff for this compound.

The compound reacts with N₂, forming a N₂-bridged dimer.

e) Draw the structure of this product.

f) This compound produces no EPR spectrum. Provide a resonance structure of (e) that explains this observation.

Answer

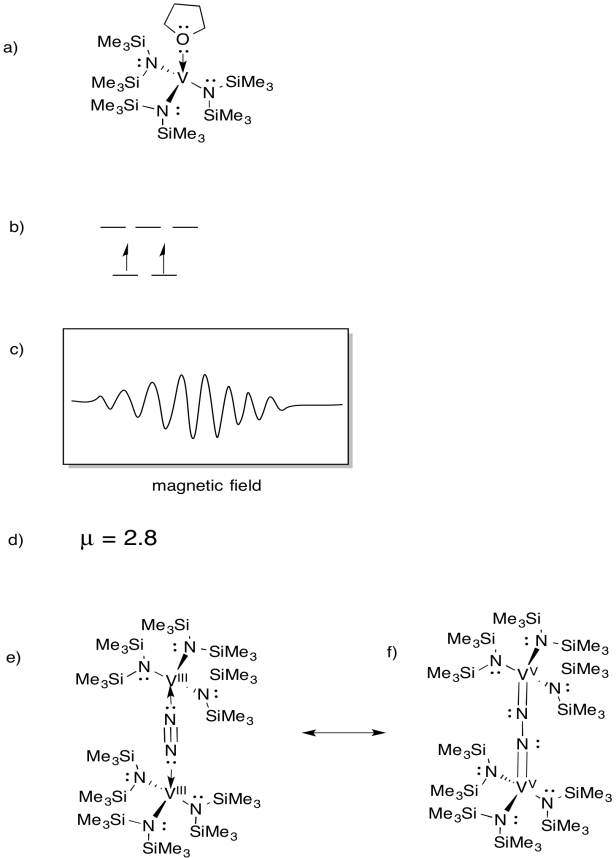
EPR spectra provided courtesy of Virtual Imagination / Slapdash Chemistry Creations.