1.3: Reduction Potential
- Page ID
- 190005
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Iron and copper are two common metals in biology, and they are both involved in electron relays in which electrons are passed from one metal to another to carry out transformations on substrates in cells. But which one passes the electron to which? Or can it go either way?
How easily one metal can pass an electron to another, or how easily one metal can reduce another, is a pretty well-studied question. There are some preferences, some of which can be easily understood.
In order to look at this question, electrochemists typically measure the voltage produced when a circuit is set up that includes an electron made of the metal in question and an electrode made of a "standard hydrogen electrode". In a standard hydrogen electrode, hydrogen gas (H2) reacts on a platinum surface to produce two electrons and two protons. The electrons travel along a wire to the other electrode. The other electrode sits in an aqueous solution containing a salt of the metal in question. How easily is the metal ion reduced by accepting the electrons from the standard hydrogen electrode? The more downhill energetically this process is, the more positive is the voltage measured in the circuit.
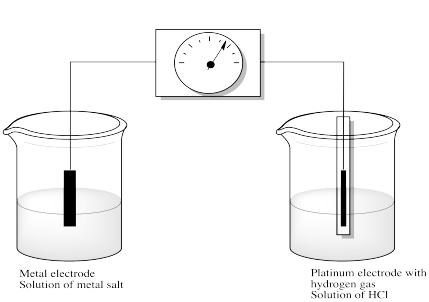
For example, we might put some copper(II) salts, such as CuSO4, into the solution together with a copper electrode. Then we would see whether the copper in solution is spontaneously reduced to copper metal. That would happen, essentially, if the copper ion is more easily reduced than a proton. Thus, an electron released by hydrogen flows from the platinum electrode to the copper electrode and is picked up by copper ions waiting in solution.
Otherwise, what would happen if the reaction were not spontaneous? If no reaction occurred at all, maybe there would be no voltage. However, if the opposite reaction were to occur -- if copper were able to provide an electron to convert protons into molecular hydrogen -- then current would flow through the circuit in the opposite direction. A voltage would register, but it would be negative.
As it happens, the reaction is spontaneous, the hydrogen does send electrons through the wire, turning into protons in the process, and at the other end of the wire, the copper ion is converted into copper metal, putting another layer on the surface of the electrode. The voltage is about 0.34V.
This is a comparative, rather than absolute, measurement. We are measuring the intrinsic potential of an electron to be transferred from one species, a hydrogen molecule, to another, a Cu(II) ion.
It is also an intensive, rather than extensive, property. It does not matter how much copper we have, or how much hydrogen; the electron still has the same natural tendency to flow from the hydrogen to the copper.
The results of many such studies, carefully measured under specific conditions for maximum reproducibility, are gathered in a table of reduction potentials. The reactions are referred to as "half-reactions" because they each provide only half the picture of what is going on. The electron in each reaction doesn't come from nowhere; every reaction in the table would involve transfer of an electron from elemental hydrogen to form a proton.
| Half Reaction (species are aqueous unless noted otherwise) | Potential, Volts |
|
\[\ce{Li^{+} + e^{-} -> Li (s)} \nonumber\] |
- 3.04 |
|
\[\ce{Al(OH)3 (s) + 3e^{-} -> Al (s) + 3OH^{-}} \nonumber\] |
- 2.31 |
| \(\ce{Al^{3+} + 3e^{-} -> Al (s)}\) | - 1.662 |
| \(\ce{Zn^{2+} + 2e^{-} -> Zn (s)}\) | - 0.762 |
|
\[\ce{Fe^{2+} + 2e^{-} -> Fe (s)} \nonumber\] |
- 0.44 |
|
\[\ce{CO2(g) + 2H^{+} 2e^{-} -> CO(g) H2O} \nonumber\] |
- 0.11 |
|
\[\ce{SnO (s) 2H^{+} + 2e^{-} -> Sn(s) + H2O} \nonumber\] |
- 0.10 |
|
\[\ce{2H^{+} + 2e^{-} -> H2 (g)} \nonumber\] |
0.00 |
|
\[\ce{Fe3O4(s) + 8H^{+} + 8e^{-} -> 3Fe(s) + 4H2O} \nonumber\] |
+ 0.085 |
|
\[\ce{Cu^{2+} + 2e^{-} -> Cu^{0}} \nonumber\] |
+ 0.34 |
|
\[\ce{Ag2O (S) + H2O + 2e^{-} -> 2Ag (s) + 2OH^{-} aq} \nonumber\] |
+ 0.342 |
|
\[\ce{O2 (g) + 2H2O + 4e^{-} -> 4OH^{-}} \nonumber\] |
+ 0.40 |
|
\[\ce{CO(g) + 2H^{+} + 2e^{-} -> C(s) + H2O} \nonumber\] |
+ 0.52 |
|
\[\ce{Cu^{+} + e^{-} -> Cu(s)} \nonumber\] |
+ 0.52 |
|
\[\ce{MnO4^{-} + 2H2O + 3e^{-} -> MnO2(s) + 4OH^{-}} \nonumber\] |
+ 0.59 |
|
\[\ce{Fe^{3+} + e^{-} -> Fe^{2+} (aq)} \nonumber\] |
+ 0.77 |
|
\[\ce{Ag^{+} + e^{-} -> Ag(s)} \nonumber\] |
+ 0.796 |
|
\[\ce{MnO2 + 4H^{+} + 2e^{-} -> Mn^{2+} + 2H2O} \nonumber\] |
+ 1.23 |
|
\[\ce{MnO4^{-} + 4H^{+} + 3e^{-} -> MnO2(s) + 2H2O} \nonumber\] |
+ 1.70 |
|
\[\ce{Au^{+} + e^{-} -> Au(s)} \nonumber\] |
+ 1.83 |
|
\[\ce{F2(g) + e^{-} -> 2F^{-}} \nonumber\] |
+ 2.87 |
Much more extensive tables of reduction potentials can be found; for example, see the following Wikipedia data page.
A positive reduction potential indicates a spontaneous reaction. That makes sense, for instance, in the reaction of fluorine to give fluoride ion. For that reaction, E0 = 2.87 V. Of course, fluorine is a very electronegative element, and it will spontaneously accept an electron to obtain a noble gas configuration.
A negative reduction potential, on the other hand, indicates a reaction that would not occur spontaneously. For example, we would not expect lithium cation to accept an electron. We are used to thinking about alkali metals easily giving up their electrons to become cations. The reduction of lithium ion has a reduction potential E0 = -3.04 V. This reaction would only occur if it were driven by an expenditure of energy.
The opposite reaction, on the other hand, would be the oxidation of lithium metal to give a lithium cation. That reaction would occur spontaneously, and would have a spontaneous "oxidation potential". In fact, that value is + 3.04 V. The oxidation potential is always the same magnitude of the reduction potential for the reverse reaction, but with the opposite sign.
These signs may seem counter-intuitive if you are used to thinking of free energy changes. A negative free energy change means energy is lost in a reaction. A positive free energy change means energy must be put into a reaction to drive it forward. In fact, reduction potential and free energy are closely linked by the following expression:
\[\Delta G = -nFE^{0} \nonumber\]
in which n = number of electrons transferred in the reaction; F = Faraday's constant, 96 500 Coulombs/mol.
So, a positive reduction potential translates into a negative free energy change.
Note that reduction potentials are pretty sensitive to changes in the environment. Factors that may stabilize one particular metal ion may not have the exact same effect on another, and so the preference for one state versus another will be altered slightly under different conditions.
For example, permanganate ion (MnO4-) has a more positive reduction potential under "acidic conditions" (with excess protons in solution) compared to "basic conditions" (with a paucity of protons in solution and instead an excess of hydroxide ion). The reduction potential under acidic conditions is +1.23V, compared to +0.59 V under basic conditions.
Tables of reduction potentials are also useful in assessing the opposite reaction. For example, lithium metal spontaneously reduces protons to produce hydrogen gas, becoming lithium ion in turn. The potential for that reaction is simply the opposite of the reduction potential of lithium ion; this is called the oxidation potential of lithium metal. The more positive a metal's oxidation potential, the more easily it is oxidized. However, we don't need a separate table of those values; they are just the opposite of the reduction potentials. Reactions with negative reduction potentials easily go backwards, reducing the proton to hydrogen gas by taking an electron from the reducing agent.
However, the most important use of standard reduction potentials is combining them to find out the potential of new reactions.
For example, when it says in the table that
\[\ce{Cu^{+} + e^{-} -> Cu(s)}\) \(E^{0}= 0.53V \nonumber\]
It really means that is the potential produced for a specific reaction involving electron transfer between hydrogen and copper ion:
\[\ce{H2(g) + 2Cu^{+} -> 2Cu(s) + 2H^{+}}\) \(E^{0} = 0.53V \nonumber\]
And when it says that
\[\ce{Fe^{2+} + 2e^{-} -> Fe(s)}\) \(E^{0}=-0.44V \nonumber\]
It really means that
\[\ce{H2(g) + Fe^{2+} -> Fe(s) + 2H^{+}}\) \(E^{0} = -0.44V \nonumber\]
But now we know that reaction is endergonic, with a negative reduction potential and a positive free energy change. However, the reverse reaction
\[\ce{Fe(s) + 2H^{+} -> H2(g) + Fe^{2+}}\) \(E^{0}=0.44V \nonumber\]
has a positive reduction potential and would proceed easily.
Now, if we combine those previous reactions, simply by adding them together
\[\ce{H2(g) + 2Cu^{+} + Fe(s) + 2H^{+} -> H2(g) + Fe^{2+} + 2Cu(s) + 2H^{+}}\) \(E^{0} = 0.44 + 0.53V \nonumber\]
and simplifying
\[\ce{2Cu^{+} + Fe(s) -> Fe^{2+} + 2Cu(s)}\) \(E^{0} = 0.97V \nonumber\]
That means the hydrogen reaction doesn't need to be involved at all. It's just a common reference point for all the other reactions. If we know how far uphill (or downhill) any two reactions are compared to that one, then we know how they compare to each other, too.
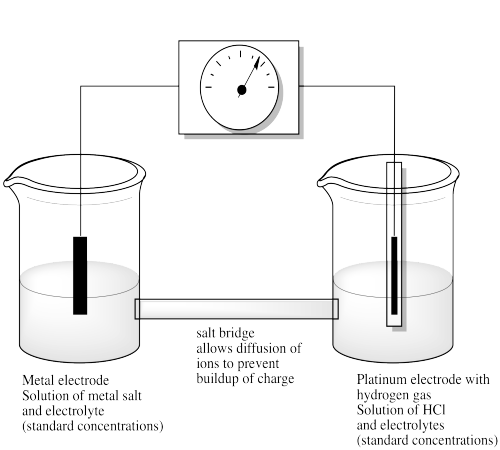
We should note that electrochemistry is a business that demands great care. There are a number of factors that can cause variations in the potential that is measured, and so we need to be very careful to control for those factors. For example, if there is a buildup of charge in one solution or another (because we are taking cations out of solution in one case and putting them into solution in the other), the ability to remove more electrons at one electrode and deliver them at another may be hindered. For that reason, a "salt bridge" is incorporated into the design of the system; this bridge allows ions to diffuse from one cell to the other in order to keep charge balanced. Also, the solutions are maintained at a standard concentration to make sure measurements are always made in comparable circumstances. Finally, non-reactive electrolytes (salts) are added to solution to aid in conductivity and maintain a constant ionic strength.
Calculate oxidation states to confirm that the manganese ion is being reduced in the following reaction:
\[\ce{MnO4^{-} + 2H2O + 3e^{-} -> MnO2(s) + 4OH^{-}} \nonumber\]
- Answer
-
MnO4- : 4 x O2- (= 8-) + Mn7+ = 1- overall
MnO2 : 2 x O2- (= 4-) + Mn4+ = neutral overall
difference = 3 e-
Balance the following half reactions by adding the right number of electrons to one side or the other, based on oxidation state. Then add water molecules and protons to help balance oxygens and overall charge.
- S2O82- → 2 SO42-
- HPO32- → P
- Ti2O3 → 2 TiO
- N2 → 2 NH2OH
- Answer a
-
a) SO42- : 4 x O2- (= 8-) + S6+ = 2- overall
S2O82- : 8 x O2- (= 16-) + 2 x S7+ (= 14+) = 2- overall
difference = 1 e- per S, or 2 e- overall
S2O82- + 2 e- → 2 SO42-
- Answer b
-
b) HPO32- : 3 x O2- (= 6-) + H+ + P3+ = 2- overall
P : P(0)
difference = 3 e-
HPO32- + 3 e- + 5 H+ → P + 3 H2O
- Answer c
-
c) Ti2O3 : 3 x O2- (= 6-) + 2 x Ti3+ (= 6+) = neutral overall
TiO : O2- + Ti2+ = neutral overall
difference = 1 e- per Ti, or 2 e- overall
Ti2O3 + 2 e- + 2 H+ → 2 TiO + H2O
- Answer d
-
d) N2 : N(0)
NH2OH : O2- + 3 x H+ (= 3+) + N- = neutral overall
difference = 1 e- per N, or 2 e- overall
N2 + 2 e- + 2 H+ + 2 H2O → 2 NH2OH
Why is the reduction potential of Li+ so negative?
- Answer
-
Lithium is an alkali metal, in the first column of the periodic table. It has a relatively low ionization energy because it has a noble gas configuration as a cation. That noble gas configuration is stable because of the relatively large number of nuclear protons and a relatively short distance between the nucleus and the outermost shell of electrons. In lithium metal, the outermost electron is relatively far from the nucleus and so it is at a relatively high energy, and easily lost.
Why is the reduction potential of F2 so positive?
- Answer
-
Fluorine is a halogen, with a relatively high electron affinity. It easily gains an electron to get to a noble gas configuration as a fluoride anion. That noble gas configuration is stable because of the relatively large number of nuclear protons and a relatively short distance between the nucleus and the outermost shell of electrons.
Rank the following metals from most easily oxidized to least easily oxidized: gold, iron, aluminum, copper, lithium.
- Answer
-
From most easily oxidized to least easily oxidized: Li > Al > Fe > Cu > Au
Calculate reduction potentials for the following reactions:
- \(\ce{Au + Ag^{+} -> Au^{+} + Ag}\)
- \(\ce{Zn + Fe^{2+} -> Zn^{2+} + Fe}\)
- \(\ce{Li + Cu^{+} -> Li^{+} + Cu}\)
- \(\ce{Ag + Fe^{3+} -> Ag^{+} + Fe^{2+}}\)
- Answer a
-
a) E0 = + 0.796 (Ag+/Ag) - 1.83 (Au/Au+) = -1.034 V (no forward reaction)
- Answer b
-
b) E0 = - 0.44 (Fe2+/Fe) + 0.762 (Zn/Zn2+) = + 0.0322 V (forward reaction)
- Answer c
-
c) E0 = + 0.52 (Cu+/Cu) + 3.04 (Li/Li+) = + 3.56 V (forward reaction)
- Answer d
-
d) E0 = + 0.77 (Fe3+/Fe2+) - 0.796 (Ag/Ag+) = - 0.026 V (no forward reaction)
In general, if one reaction is combined with the reverse of a reaction above it in the table, will the overall reaction be spontaneous? What about if a reaction is combined with the reverse of a reaction below it?
- Answer
-
When the table of standard reduction potentials is displayed with the most negative value at the top and the most positive value at the bottom, any given half-reaction will go forward if it is coupled with the reverse of a half-reaction that lies above it in the table. The opposite is not the case; no half reaction will go forward if it is coupled with the reverse of a half-reaction below it in the table.


