1.3: Activation Barriers
- Page ID
- 189834
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Why do reactions take place at different rates? Why do some happen quickly, and others proceed very slowly? Why might the same reaction proceed at different rates under different conditions? There are a number of factors that influence reaction rates, but the first one that we will look at is the activation barrier.
An activation barrier is a sort of energetic hurdle that a reaction must get over. Some reactions have higher hurdles and some have lower hurdles. It's much easier to get over lower hurdles, so reactions with low activation barriers can proceed more quickly than ones with higher activation barriers.
- A low activation barrier allows a reaction to happen quickly.
- A high activation barrier makes a reaction go more slowly.
A reaction can be exergonic overall (it can give off energy), but it will generally still have an activation barrier at the beginning. Even if the compounds go down in energy by the end of the reaction, they will generally go up in energy before that happens.
- Even if a reaction gives off energy overall, some energy must be put in at first to get the reaction started.
This situation is a little like investing in a business. A business generally requires some sort of financial investment to get started. If the business is successful, it will eventually make products and pay money back to the investors. If the business is unable to make back its initial investment, it may fail.
Reactions require some initial investment of energy. This energy may come from surrounding molecules or the environment in general. If the reaction is successful, it will proceed to make products and it will give energy back to its surroundings.
- It always "costs" a molecule energy to enter into a reaction; it "borrows" that energy from its environment.
- That initial investment of energy may be "paid back" as the reaction proceeds.
All reactions must overcome activation barriers in order to occur. The activation barrier is the sum of the energy that must be expended to get the reaction going. An activation barrier is often thought of, cartoonishly, as a hill the molecule has to climb over during the reaction. Once, there, it can just slide down the other side of the hill to become products. At the top of the hill, the molecule exists in what is called the "transition state". At the transition state, the structure is somewhere between its original form and the structure of the products.
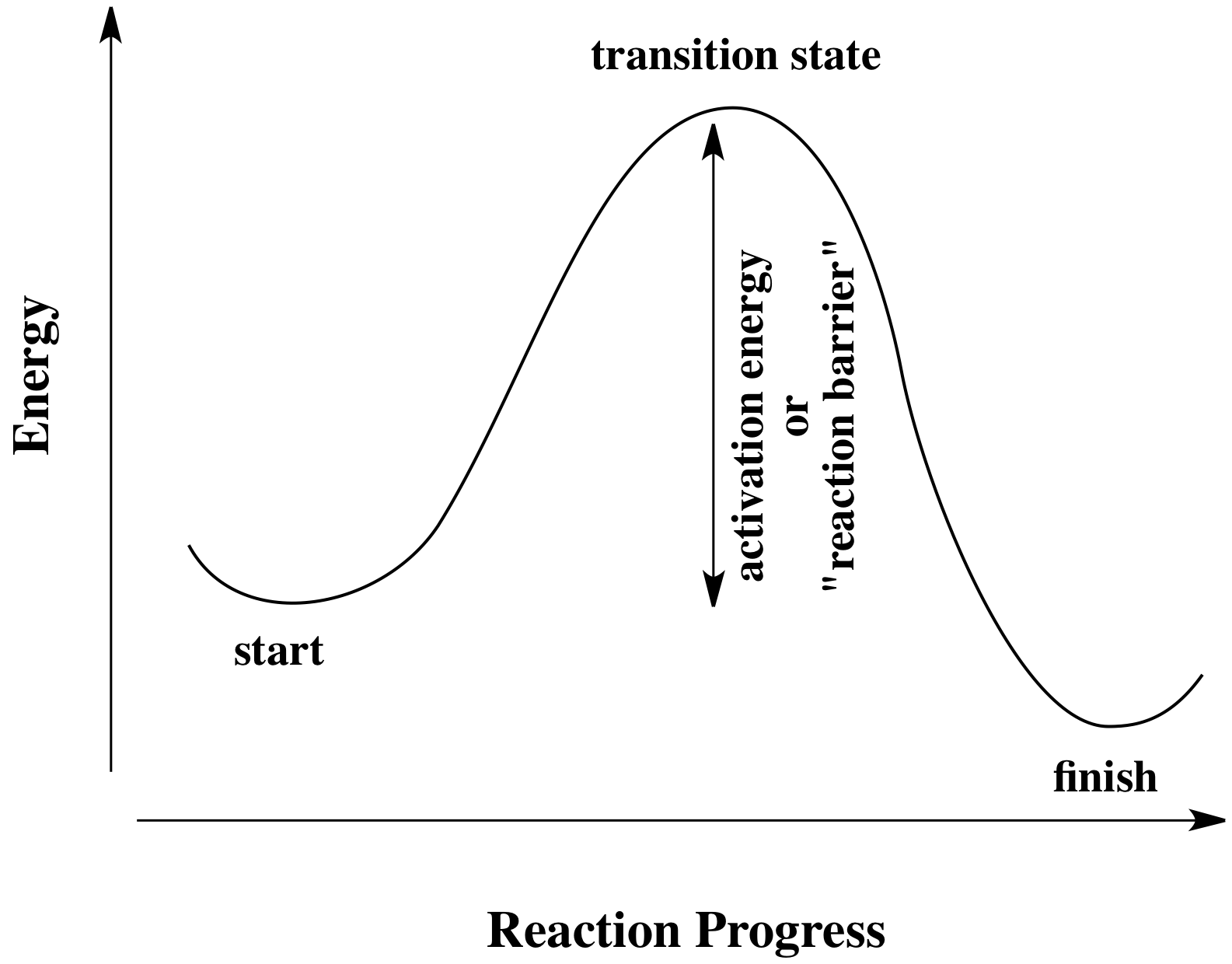
The type of diagram shown above is sometimes called a "reaction progress diagram". It shows energy changes in the system as a reaction proceeds. One or more activation barriers may occur along the reaction pathways, as various elementary steps occur in the reaction.
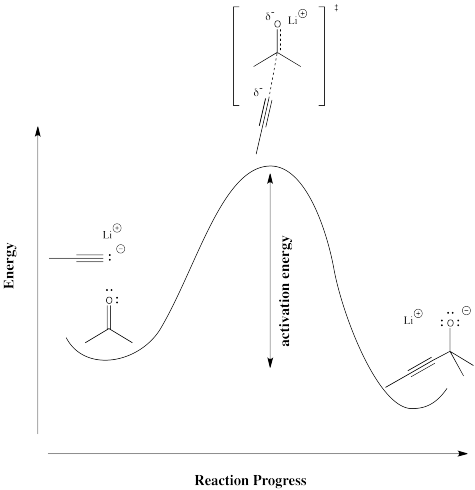
In order to see more concretely what terms like "reaction progress" and "transition state" mean, let's look at a real reaction. Suppose a nucleophile, such as an acetylide ion, donates its electrons to an electrophilic carbonyl. The π bond breaks and an alkoxide ion is formed.
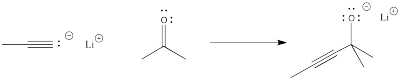
The reaction progess simply refers to how far the reaction has proceeded. Is it just starting out, is it almost finished, is it just halfway there? The transition state refers specifically to the highest energy point on the pathway from reactants to products. It refers to the structure at that point, and the energy associated with that structure.
In the following diagram, the term "reaction progress" has been replaced by an illustration that shows how far the reaction has proceed by that point in the energy curve that is above the reaction drawing. The structure in the square brackets is the transition state, coresponding to the highest point on the curve. The "double dagger" symbol (a little bit like a Patriarchal or Russian Orthodox cross, with two crosspieces on a vertical post) is the symbol that tells you that you are looking at a transition state structure.
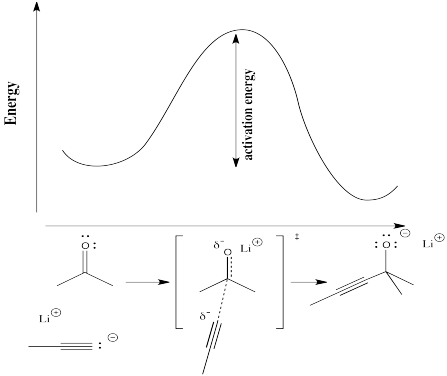
The transition state doesn't refer to a regular chemical structure. It doesn't necessarily obey the rules of Lewis structures, because some new bonds have started to form and some old bonds have started to break; you can't really draw partial bonds in a Lewis structure.
Physically, the transition state structure is not something that can be isolated and stored in a bottle. Because it sits at the top of an energy curve, the transition state is motivated to turn into something else. No matter what direction it goes to change its structure, it will go to lower energy. Remember, things always proceed to lowest energy if possible. As soon as the transition state forms, it will either slide back into the original starting materials or slip forward into the final products.
- The transition state is inherently a high-energy, unstable structure, with a very short lifetime. As soon as it comes into existence, it disappears again.
Draw what you think the transition state might look like for the following elementary reactions.
More commonly, reaction progress diagrams aren't drawn like the one above. Instead, structures of reactants, transition states and products are simply shown along the potential energy curve, as shown below.
Reactions don't always happen in one step. Sometimes there is an intermediate, or more than one. An intermediate differs from a transition state in that it has finite lifetime. Although it is not as stable as the reactants or the products, it is stable enough that it does not immediately decay. Going either forward to products or back to reactants is energetically uphill.
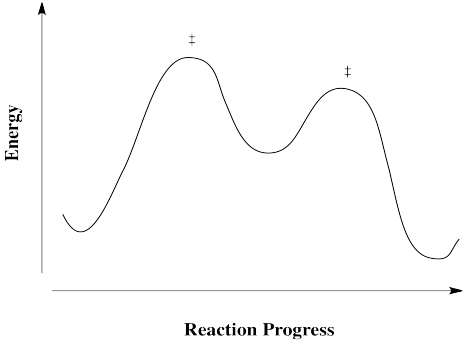
Draw reaction progress diagrams for the following reactions. Note that the reactions may be composed of more than one elementary step.
Rate Constant
There is a measurable parameter that can be used to get an idea about the activation barrier of a reaction. It is called the rate constant. The rate constant for a reaction is related to how quickly the reaction proceeds. A large rate constant corresponds to a very fast reaction. A very small rate constant corresponds to a slow one.
- The rate constant is an index of the speed of the reaction.
Rate constants have different units depending on how the reaction proceeds, but just to give you a feel for how they vary, a reaction with a "first order" rate constant of 0.001 s-1 (or 10-3 s-1; you'll learn what "first order" means later) would be over in about an hour. A reaction with a first order rate constant of 10-6 s-1 might take a couple of weeks.
The rate constant gives direct insight into what is happening at the transition state, because it is based on the energy difference between the reactants and the transition state. Based on that information, we get some ideas of what is happening on the way to the transition state.
The rate constant can be broken down into pieces. Mathematically, it is often expressed as
\[k = \frac{RT}{Nh} e^{- \Delta \frac{G}{RT}} \nonumber\]
In which R = the ideal gas constant, T = temperature, N = Avogadro's number, h = Planck's constant and D G = the free energy of activation.
The ideal gas constant, Planck's constant and Avogadro's number are all typical constants used in modeling the behaviour of molecules or large groups of molecules. The free energy of activation is essentially the energy requirement to get a molecule (or a mole of them) to undergo the reaction.
For each of the following pairs, use < or > to indicate which quantity is larger.
a) e 2 or e 10
b) e 1/4 or e 1/2
c) e -3 or e -4
d) e -1/2 or e -1/3
- Answer a
-
e 2 < e 10
- Answer b
-
e 1/4 < e 1/2
- Answer c
-
e -3 > e -4
- Answer d
-
e -1/2 < e -1/3
Note that k really depends on just two variables:
- rate constant depends on ΔG or the energy required for the reactionli>
- rate constant depends on T or the temperature of the surroundings, which is an index of how much energy is available
The ratio of activation free energy to temperature compares the energy needed to the energy available. The more energy available compared to the energy needed, the lower this ratio becomes. As a result, the exponential part of the function becomes larger (since the power has a minus sign). That makes the rate constant bigger, and the reaction becomes faster.
Large groups of molecules behave like populations of anything else. They have averages, as well as outliers on the high and low end. However, the higher the temperature, the more energy a group of molecules will have on average.
In the following drawing, the blue curve represents the energy content in a population of molecules at low temperature. The peak of the curve is near the average energy for this collection of molecules. Some of the molecules have more energy than average (they are further to the right on the blue curve) and some have less (further to the left).
The black slice through this curve indicates how much energy is needed to get over the activation barrier for a particular reaction. Notice that, at low temperature, not that many molecules have enough energy to get over the barrier at any one time. The reaction will proceed very slowly. Nevertheless, more energy is probably available from the surroundings, and so after some time most of the molecules will have obtained enough energy so that they can eventually hop over the barrier.
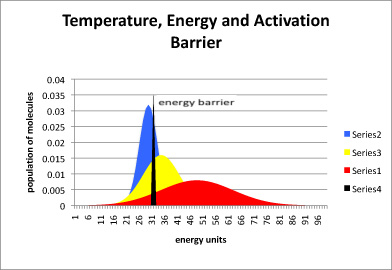
The yellow curve represents molecules at a higher temperature, and the red curve is a population at a higher temperature still. As the temperature is increased, larger and larger fractions of the molecules have enough energy to get over the activation barrier, and so the reaction proceeds more quickly.
- the rate constant compares energy needed to energy available
- based on that comparison, a specific fraction of the population will be able to react at a time
Free Energy of Activation
There is really more to the activation energy than we have seen so far. The activation free energy is constant for a given reaction at a given temperature. But at different temperatures, ΔG changes. Just as in thermodynamics, it can be broken down in turn to:
\[\Delta G = \Delta H - T \Delta S \nonumber\]
in which ΔH = activation enthalpy and ΔS = activation entropy.
The activation enthalpy is the part that corresponds most closely with the energy required for the reaction, the way we have been describing the activation barrier so far.
The activation entropy deals with how the energy within the molecule must be redistributed for the reaction to occur. One of the major factors influencing energy distribution over the course of the reaction is molecular geometry.
For example, suppose two molecules need to come together for a reaction to take place. They need to collide with each other. However, a reaction might not happen each time the molecules collide. Sometimes, the molecules may be pointing the wrong way when they bump into each other, so that the reaction can't occur. Often, atoms need to be lined up in the proper place where they will be forming a new bond.
When molecules are restricted to only certain orientations or geometries, they have fewer degrees of freedom. With fewer degrees of freedom, energy can be stored in fewer ways. As a result, there is often an entropy cost in initiating a reaction.
On the other hand, a reaction might start in a very different way, with one molecule breaking a bond and dividing into two pieces. Because each individual piece can move independently from the other, the degrees of freedom increase. Energy can be stored in more ways than they could be before the reaction started. As a result, although this reaction would still have an activation barrier, the entropy component may actually lower that barrier a little bit.
In the following drawings, one orientation of reactants is more likely to lead to the product shown. Select which one will be most successful in each set and explain what is wrong with each of the others.

- Answer a
-
Orientation (i) looks most likely to result in connection of the oxygen to carbon with displacement of bromide. In orientation (iii), the oxygen appears ready to collide with the bromine atom. and in oreientation (ii), it may collide with a hydrogen atom.
In addition, you will see later that bringing the the oxygen in along the C-Br axis (but away from the bromine) is also more likely to break the C-Br bond, for reasons involving molecular orbital overlap.
- Answer b
-
Orientation (ii) looks like the carbon anion in the acetylide ion is most likely to bond with the carbonyl carbon. In option (i), the carbon is going to collide with the carbonyl oxygen. In option (iii), it may collide with the alpha carbon, next to the carbonyl. Having the nucleophile approach from outside the plane of the carbonyl, as in option (ii), lowers the chance of collision with atoms other than the carbonyl carbon.
Again, there are also molecular orbital reasons that make this approach the preferred one.
Because the activation barrier depends partly on the energy needed to break bonds as the molecule heads into the transition state, comparative bond strength can be a useful factor in getting a qualitative feel for relative activation barriers.
The metal-carbonyl (M-CO) bond strengths of the coordination complexes M(CO)6 have been estimated via photoacoustic calorimetry and are listed below, by metal.
Cr: 27 kcal/mol Mo: 32 kcal/mol W: 33 kcal/mol
a) Based on that information, sketch qualitative activation barriers for the loss of a CO ligand from Cr(CO)6, Mo(CO)6 and W(CO)6.
b) Predict the relative rates for these three reactions (fastest? slowest?).
- Answer a
-
We would expect the lowest barrier for breaking the Cr-CO bond. The barrier to break the Mo-CO bond would be just slightly lower than to break the W-CO bond.
- Answer b
-
Based on this information alone, we might expect the Cr-CO cleavage to occur most rapidly. Mo-CO cleavage would be slightly faster than W-CO cleavage.
Comparing the strengths of bonds that will be broken in a reaction is often a good way to get a first estimate of relative activation barriers.
a) Use the following bond strengths to estimate the barriers to addition of a nucleophile (such as NaBH4) to the following double bonds: C=O (180 kcal/mol); C=N (147 kcal/mol); C=C (145 kcal/mol). Make a sketch of the three reaction progress diagrams.
b) In general, C=O bonds are the most reactive of these three groups toward electrophiles, followed by C=N bonds. Are these relative barriers consistent with this observation?
c) What other factor(s) might be important in determining the barrier of the reaction?
d) Modify your reaction progress diagram to illustrate these other factors.
- Answer a
-
On this basis alone, we would expect the lowest barrier for C=C cleavage, followed by C=N and then C=O with the highest barrier.
- Answer b
-
This trend is exactly the opposite of what we just predicted based on bond strengths.
- Answer c
-
There may be a few different reasons for these differences. For example, the electrophilicity of the carbon may be a factor. Based on electronegativity differences, the C=O carbon should be most positive, the C=N carbon less so and the C=C carbon not at all. That electrophilicity may raise the reactant a little in energy.
Alternatively, there may be charge stabilization factors in the first-formed intermediate, which may be reflected in the transition state on the way there. These three differing atoms (O, N, C) are all found in a row of the periodic table, so electronegativity differences should dominate charge stability. The alkoxide ion would be most stable, the amide ion of medium stability and the alkyl anion least stable of all. That trend would lower the barrier to alkoxide formation and raise the barrier to formation of a carbon-based alkyl anion.


