5.8: Interconversion- Going Downhill
- Page ID
- 189949
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The potential energy curve linking the carboxyloids can be used as a guide to how these compounds can be interconverted. In general, it is possible to take a compound that is higher on the ski hill and convert it to a compound that is lower on the ski hill.
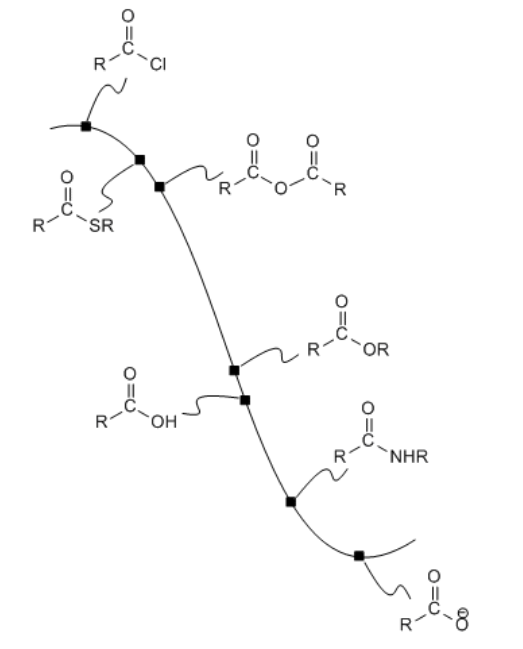
Figure \(\PageIndex{1}\): The potential energy surface linking carboxloids.
For example, acid chlorides are widely used to make other carboxyloids. By choosing the correct nucleophile, an acid chloride could be converted to any of the other derivatives. This is really the whole point of an acid chloride; it has no other function other than to provide an easy way to make other derivatives.
Acid anhydrides, also high on the potential energy curve, are also used in the same way. They could be used to make any of the derivatives lower than they are on the ski hill. In turn, acid anhydrides could conceivably be made from acid chlorides. However, because an acid anhydride plays the same role as an acid chloride -- providing a source with which to make the other derivatives -- we wouldn't normally make an acid anhydride from an acid chloride. We would either make one of the other derivatives directly from the acid chloride, or else make it from an acid anhydride that was obtained in another way.
Exercise \(\PageIndex{1}\)
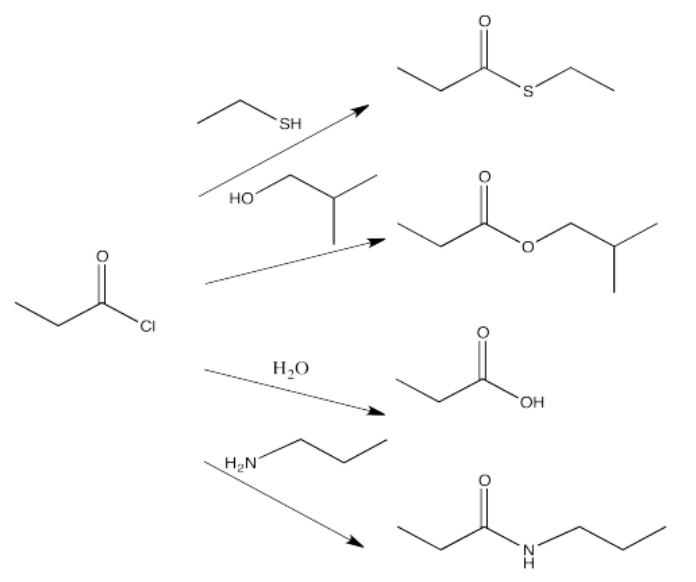
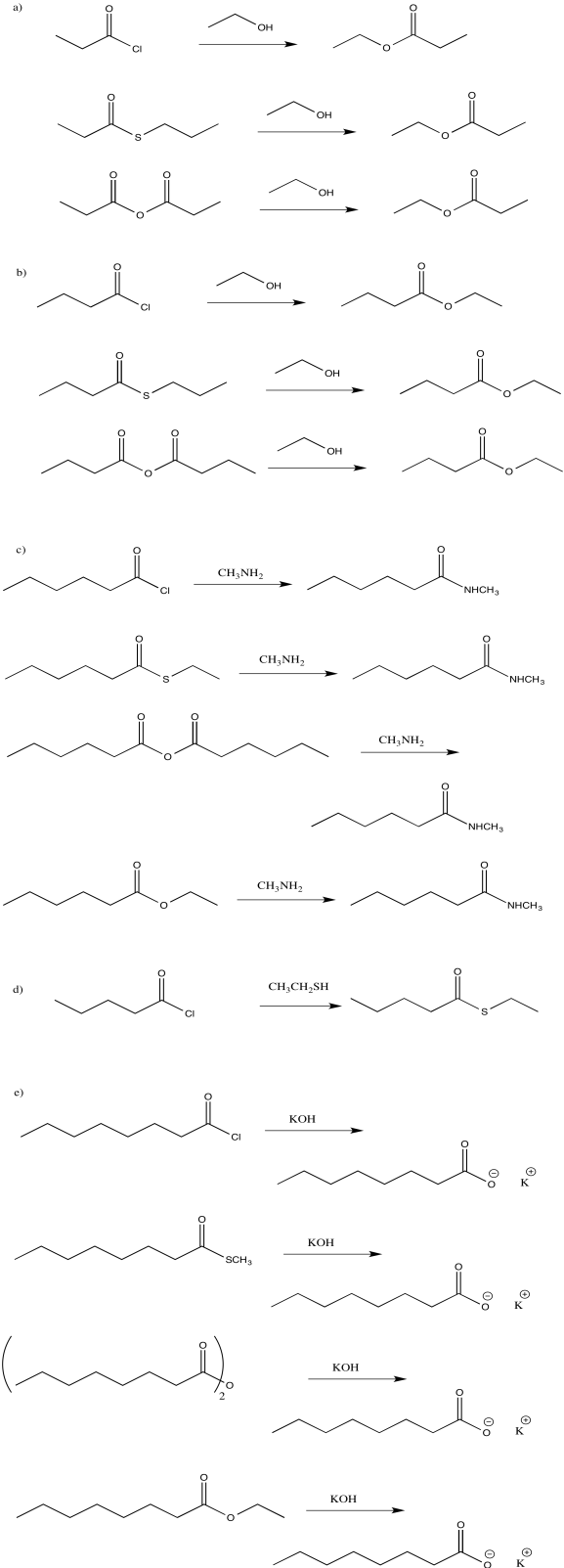
Show all of the ways that you could make the following compounds by going down the ski hill. (Show the starting material, the reagent added and a reaction arrow going to the product.) For help with names, see the appendix.
- ethyl propanoate
- butanoic acid
- N-methylhexanamide
- thioethyl pentanoate
- potassium octanoate
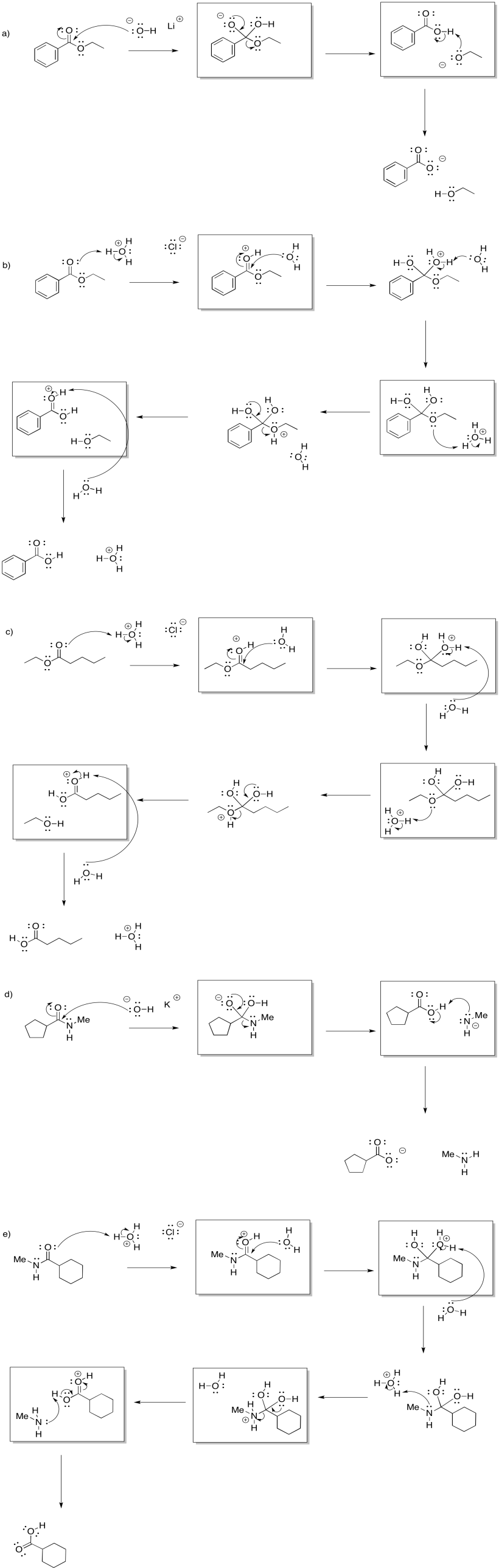
- Answer
-
Exercise \(\PageIndex{2}\)
Converting a carboxylic acid into an amide is complicated by a side reaction, as a result of which amide formation becomes an uphill process.
- Show the mechanism for the conversion of butanoic acid into N-ethylbutanamide via the addition of ethylamine.
- Show the side reaction that would easily occur between these two reactants.
- Explain why amide formation becomes an uphill process as a result of this reaction.
- Answer
-
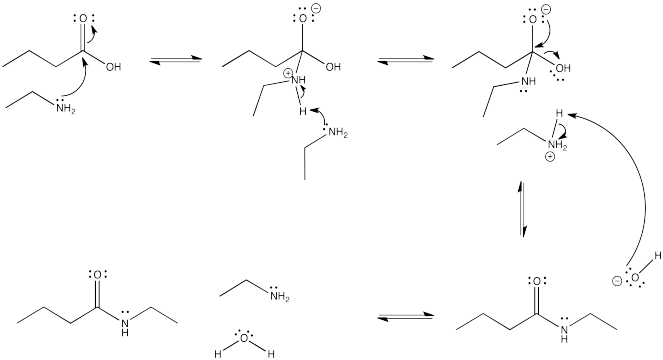
Sometimes, two carboxyloids are close enough on the ski hill that it may be possible to convert in either direction between them. In other words, there is an equilibrium between these two compounds, and the equilibrium constant is close enough to unity (K = 1) that the equilibrium can be pushed in either direction.

For selected cases, we can choose which direction the equilibrium will go by changing the reaction conditions. To do so, we can use an important concept of equilibrium: le Chatelier's principle (luh sha-TELL-yay). According to le Chatelier, if conditions in the reaction cause the reaction to move away from equilibrium, the reaction will shift direction until it is back at equilibrium again. In other words, if the actual ratio of reactants to products strays from what it ought to be, the correct reaction will occur so that the ratio returns to normal.
le Chatelier's principle should be partly intuitive. If a reaction is occurring in both reactions, there are really two reactions, one going in each direction. The ability of these reactions to occur depends partly on the amount of reactants available for the forward reaction or the reverse reaction. If extra starting materials are added (on the left side of the reaction), there is too much reactant as defined by the equilibrium constant. The denominator gets bigger and the ratio of products to reactants goes down. However, because there is extra starting material for the forward reaction, more product is quickly made, until the ratio returns to normal.
The opposite situation applies if too much product is made. From the point of view of the reverse reaction, those products of the forward reaction are really the reactants needed to go in the opposite direction. The reverse reaction has more material to work with, and this material can quickly be converted into the stuff on the left hand side of the reaction.
Exercise \(\PageIndex{3}\)
Draw the mechanism for the conversion of:
- hexyl propanoate to propanoic acid.
- propanoic acid to hexyl propanoate.
- Answer a
-
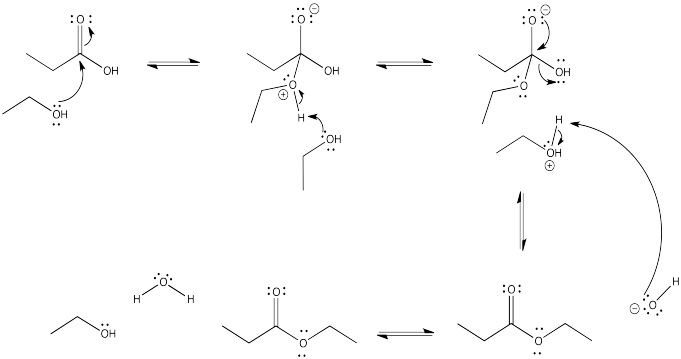
- Answer b
-
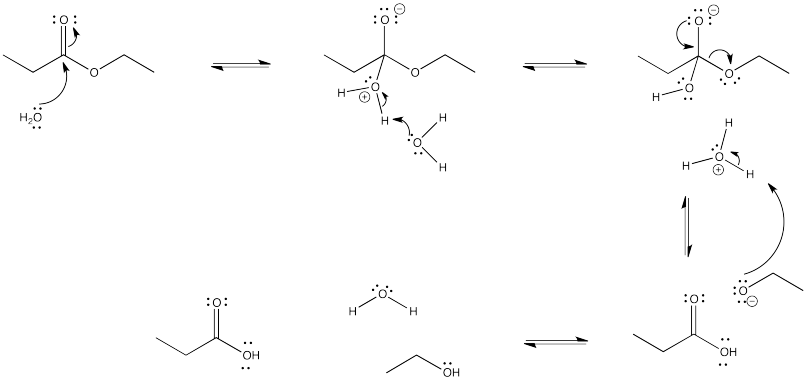
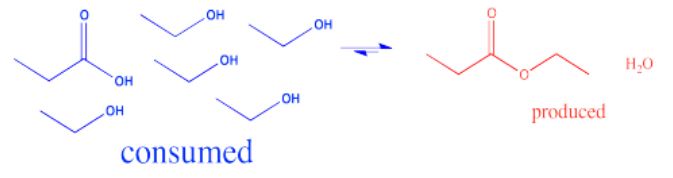
In the interconversion of carboxyloids, equilibrium can be influenced in different ways. The conversion between esters and carboxylic acids can be influenced by the solvent used for the reaction. For example, an ester might be converted to a carboxylic acid under aqueous conditions, but a carboxylic acid might be converted to an ester using the appropriate alcohol as the solvent. In other words, because water and alcohol can be viewed as reactants in these cases, adding more can shift the reaction to one side. Solvent is usually present in concentrations many tens or hundreds or thousands of times higher than the reactants and products. Changing the solvent thus has a big impact on the direction of equilibrium.
Another strategy used to influence the equilibrium involves removal of product. For example, if water is a product of the reaction, a drying agent can be added to absorb the water. Drying agents include compounds such as MgSO4 or zeolites (mixed aluminosilicates containing Al, Si, O and other metal ions such as Mg2+, Ca2+ or Ti4+).
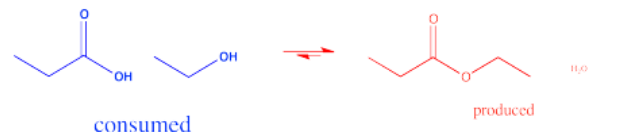
If a carboxylic acid is a product of a reaction, its concentration can be lowered by converting it to a carboxylate salt; this would happen easily in the presence of base. In either case, the disappearance of a product of the reaction (or a side product) would draw the reaction to the right in order to replace those products an re-establish the correct equilibrium ratio.
Exercise \(\PageIndex{4}\)
Show, with curved arrows, how a magnesium ion could remove water from solution.
- Answer
-

Exercise \(\PageIndex{5}\)
Show, with curved arrows, how sodium hydroxide would remove butanoic acid from solution.
- Answer
-

Exercise \(\PageIndex{6}\)
For each of the following reactions:
a. Predict the nucleophile that would be need to make this product.
b. Based on the location on the hill, would this reaction be thermodynamically favored?
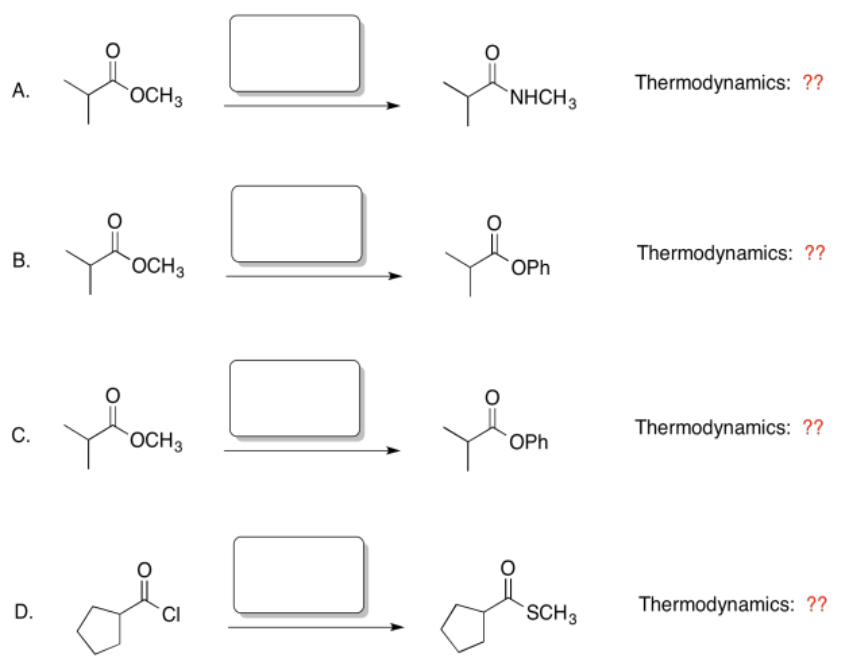
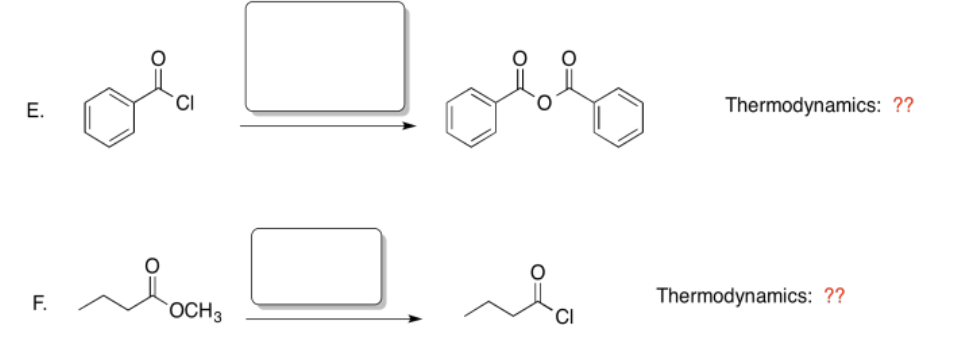
Answer-

Exercise \(\PageIndex{7}\)
Fill in the missing intermediates and add curved arrows to show electron movement.
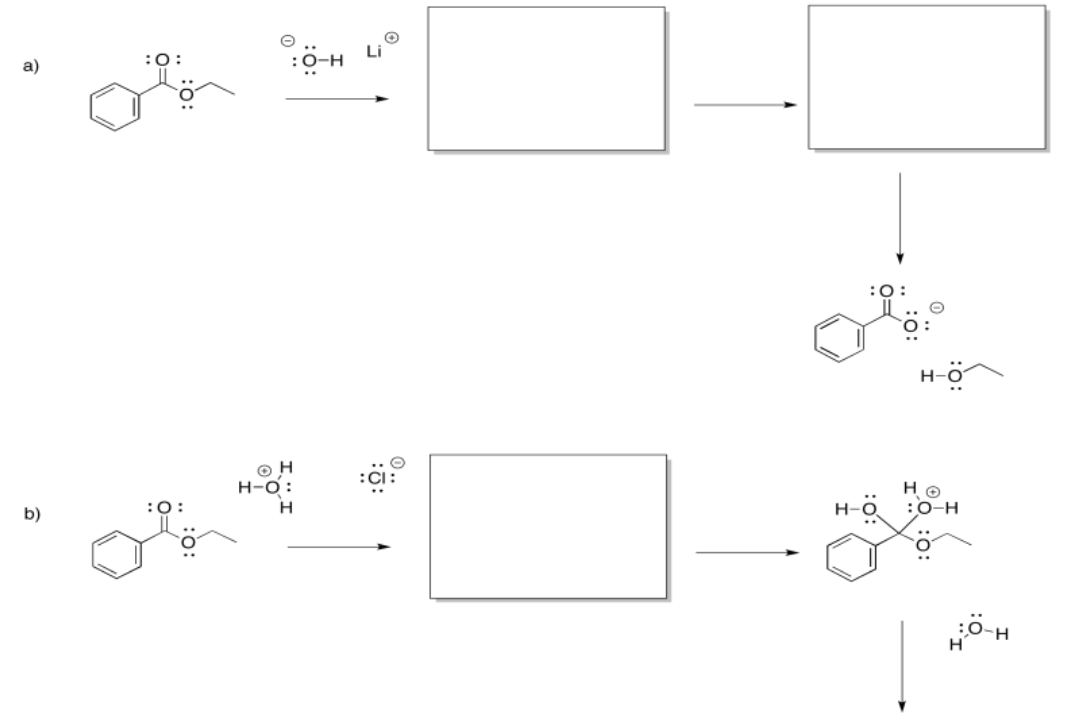
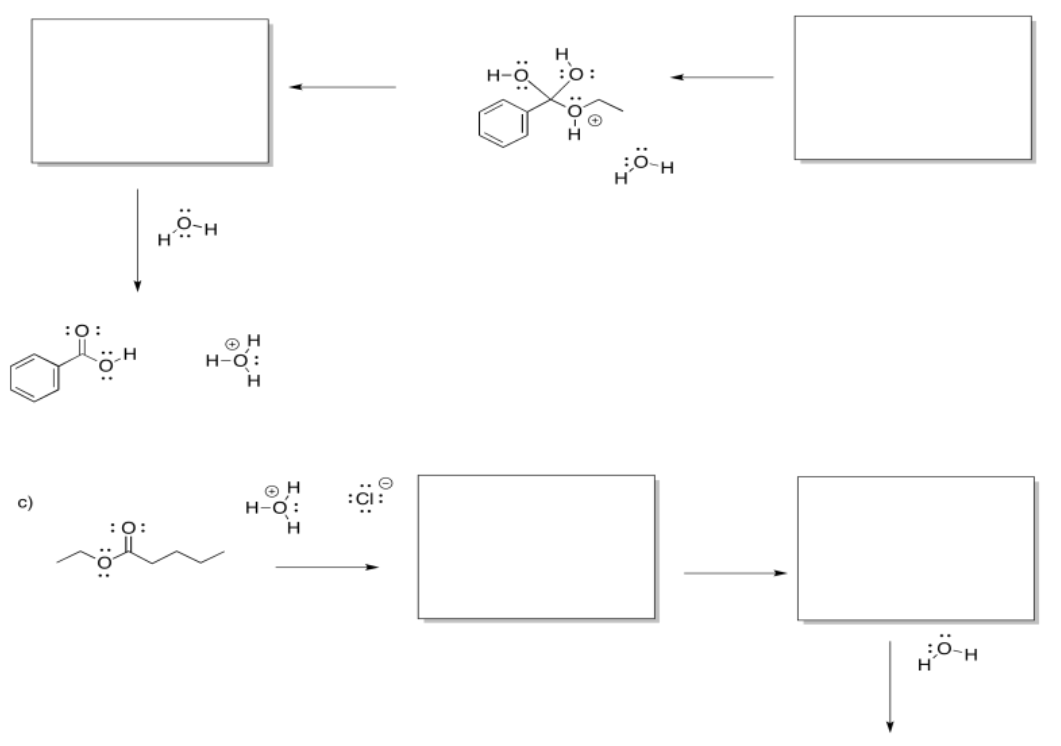
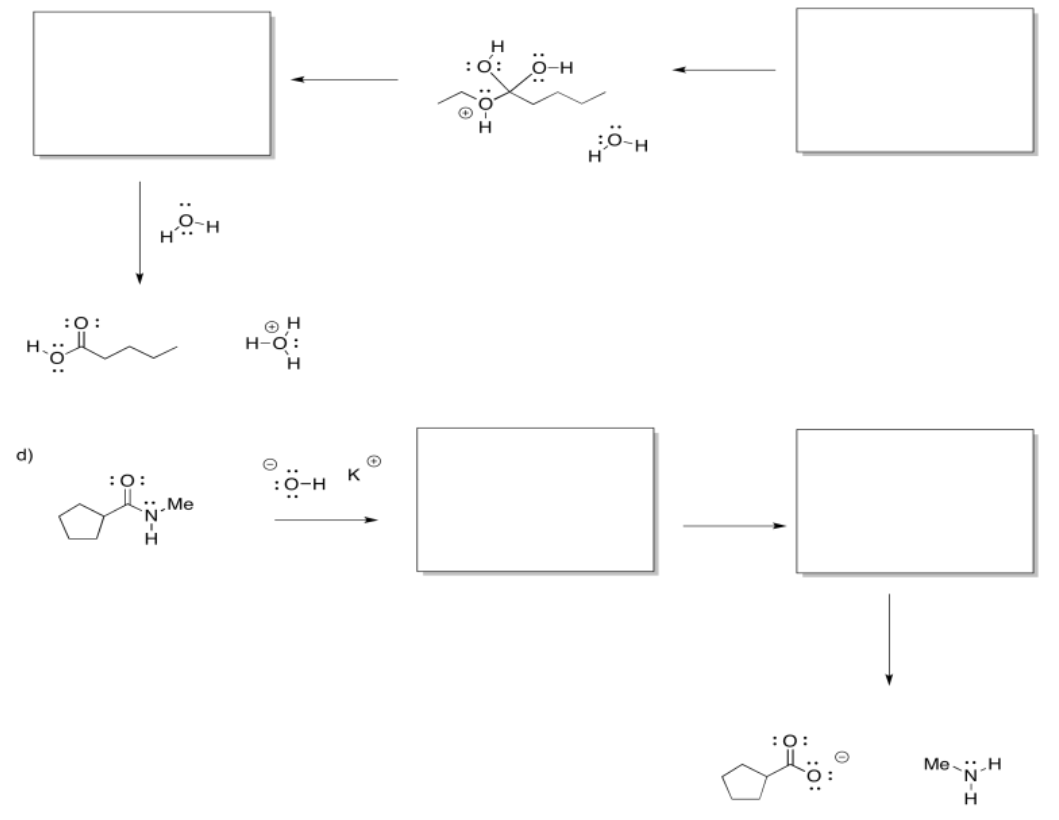
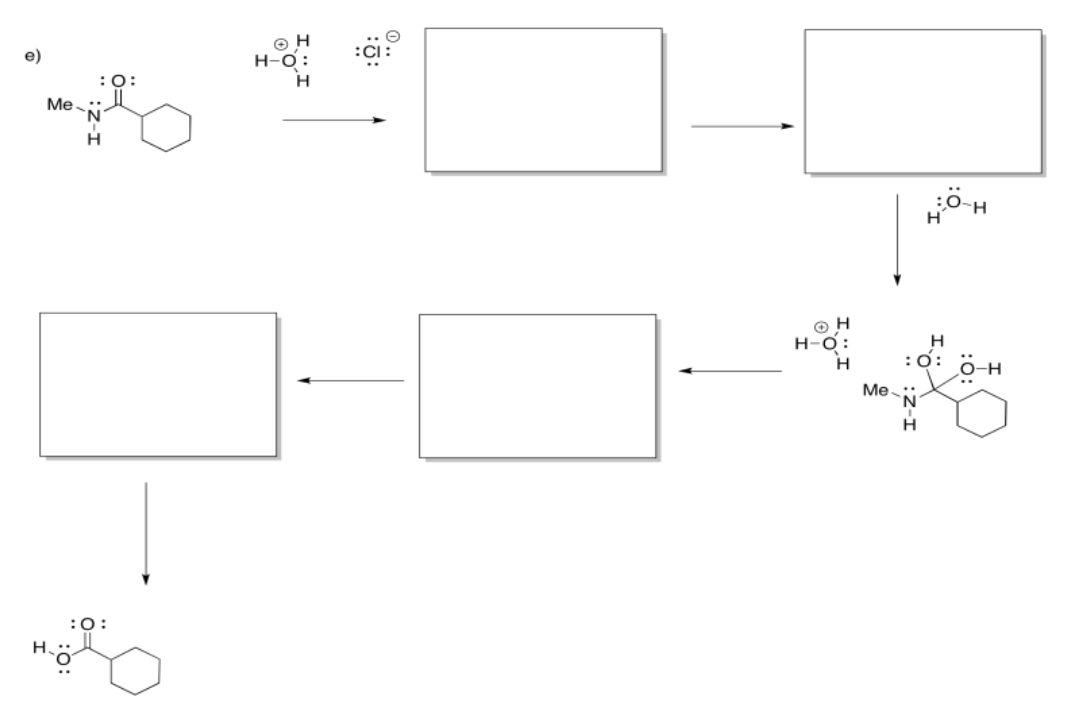
Answer-