2.15: More Solutions to Selected Problems
- Page ID
- 195683
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise 2.7.1:
a) Zn(II), because it is smaller and less polarizable.
b) K+, because it is less electronegative.
c) Fe(III), because of the higher charge.
Exercise 2.7.2:
a) Me3P, because phosphorus is larger and more polarizable than nitrogen.
b) Iodide, which is larger and more polarizable than chloride.
c) Azide, which has a more polarizable, delocalized pi bonding system.
Exercise 2.7.3:
a) ZrO2
b) CdS
c) WO3
d) ZnS
e) Cu2S
Exercise 2.7.4:
a) Hg(I) and Hg(II) are both large, polarizable ions. They are soft cations and should bind well to soft donors.
b) The most common soft donor is a sulfur atom or sulfide ion; in amino acids, that suggests cysteine or methionine.
Exercise 2.7.5:
Fe(III) is a hard cation and should bind well to oxygen donors. Enterobactin has several oxygen donors it could provide to the iron. In fact, there is a pair of OH groups on each of the benzene rings in enterobactin. These benzene rings with two OH groups next to each other are called "catechols". Because there are three of these groups in enterobactin, and there is enough space in between for the groups to fold around a central atom, enterobactin is a chelating (hexadentate) donor with a high binding constant.
Exercise 2.8.1:
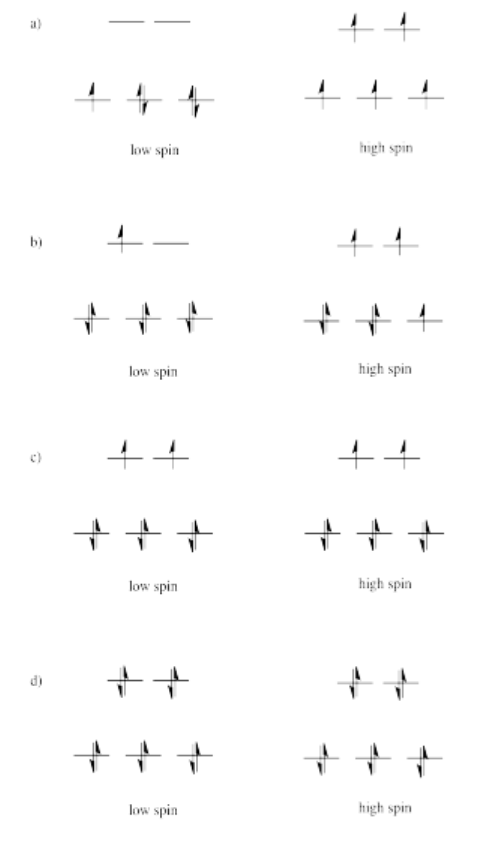
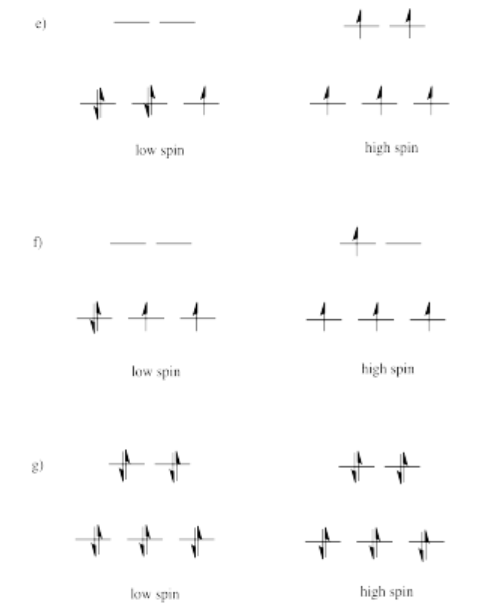
Exercise 2.8.2:
The three orbitals shown above interact a little more strongly with the ligands. The three orbitals shown below interact a little more weakly.
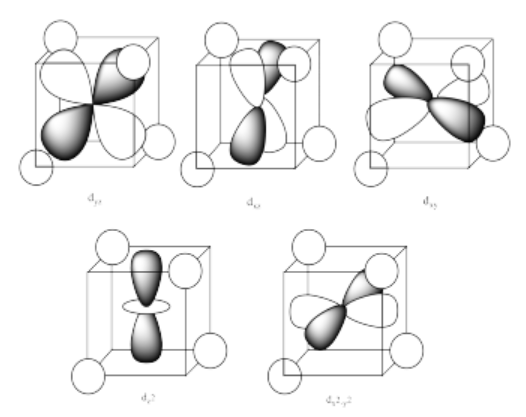
The reason for the difference in the interaction has to do with how close the nearest lobe of a d orbital comes to a ligand. There are really two possible positions: the face of a cube or the edge of a cube. If the ligands are at alternating corners of the cube, then the orbitals pointing at the edges are a little closer than those pointing at the faces of the cube.
Exercise 2.8.3:
The ligands do not overlap with the d orbitals as well in tetrahedral complexes as they do in octahedral complexes. Thus, there is a weaker bonding interaction in the tetrahedral case. That means the antibonding orbital involving the d electrons is not raised as high in energy, so the splitting between the two d levels is smaller.
Exercise 2.8.4:
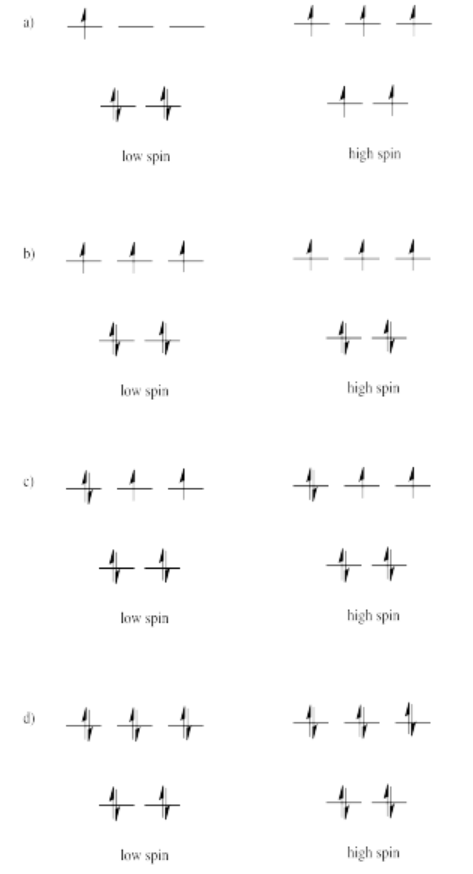
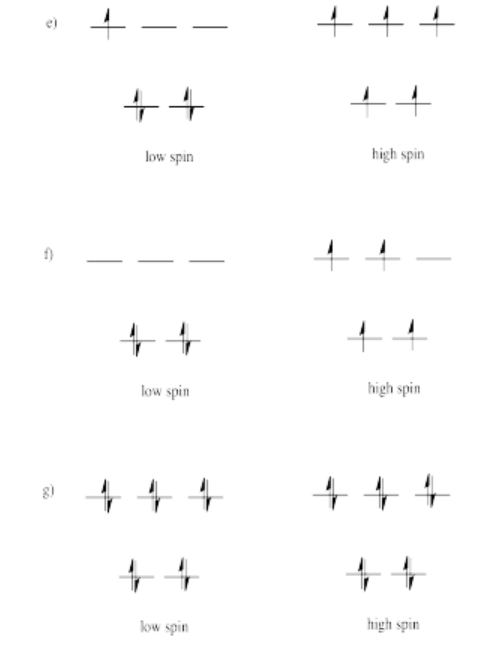
Exercise 2.8.5:
Because the d orbital splitting is much smaller in the tetrahedral case, it is likely that the energy required to pair two electrons in the same orbital will be greater than the energy required to promote an electron to the next energy level. In most cases, the complex will be high spin.
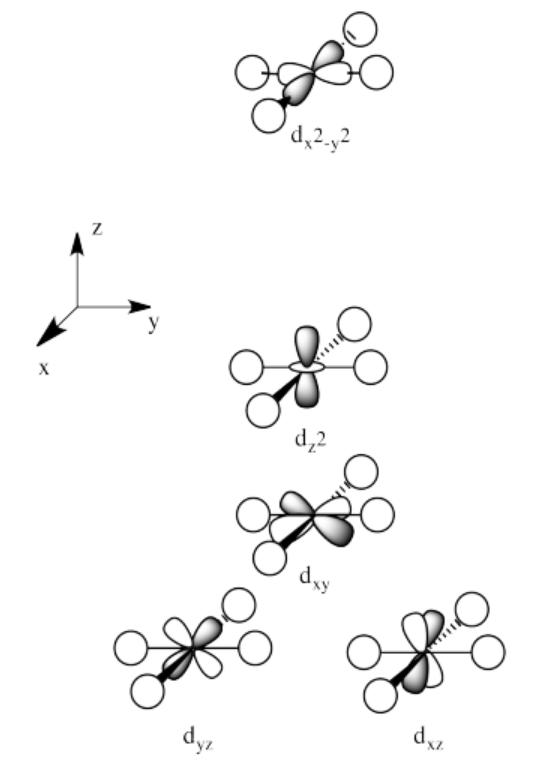
Exercise 2.8.6:
The orbitals are shown in order of energy.
Exercise 2.8.7:
a. [Fe(py)6]2+ 3d metal, M+2, pi acceptor ligand → low spin
b. [Fe(H2O)6]2+ 3d metal, M+2, pi donor ligand → high spin
c. [FeBr6]3- 3d metal, M+3, pi donor ligand → high spin
d. [Co(NH3)6]3+ 3d metal, M+3, sigma donor ligand → low spin
e. [Cu(NH3)6]2+ 3d metal, M+2, sigma donor ligand → low spin
f. [Rh(CO)6]3+ 4d metal, M+3 → low spin
g. [Cr(CO)6]3+ 3d metal, M+3, pi acceptor ligand → low spin
f. [PtCl6]2- 5d metal, M+4 → low spin
Exercise 2.8.8:
a. [Zn(NH3)4] 2+ 3d metal, d10, sigma donor ligand → tetrahedral
b. [NiCl4] 2+ 3d metal, d8, pi donor ligand → tetrahedral
c. [Ni(CN)4] 2- 3d metal, d8, pi acceptor ligand → square planar
d. [Ir(CO)(OH)(PCy3)2] 2+ 5d metal, d8 → square planar
e. [Ag(dppb)2]1+ 4d metal, d10, sigma donor ligand → tetrahedral
f. [PtCl2(NH3)2] 5d metal, d8 → square planar
g. [PdCl2(NH3)2] 4d metal, d8, M+2, sigma donor ligand → square planar
i. [CoCl4] 2– 3d metal, d7, sigma donor ligand → tetrahedral
f. [Rh(PPh3)3Cl] 5d metal, d8 → square planar
Exercise 2.9.1:
a. Fe+2
d6 low spin
\[SE = [-0.4 (6) + 0.6(0)] \Delta_{o} + 3PE \nonumber\]
\( =[-2.4] \Delta_{o} + 3PE\)
d6 high spin
\(SE = [-0.4(4) + 0.6(2)] \Delta_{o} + 1PE\)
\([-.4] \Delta_{o} + 1PE\)
b. Co+2
d7 low spin
\[SE = [-0.4(6) + 0.6(1)] \Delta_{o} + 3PE \nonumber\]
\(= [-1.8] \Delta_{o} + 3PE\)
d7 high spin
\[SE = [-0.4(5) + (0.6)2] \Delta_{o} + 2PE \nonumber\]
\(=[-.8] \Delta_{o} + 1PE\)
c. Co+3
d6 so this looks the same as Fe+2
d. Mn+2
d5 low spin
\[SE= [-0.4(5) + 0.6(0)] \Delta_{o} + 2PE \nonumber\]
\([-2.0] \Delta_o} + 2PE\)
d5 high spin
\(SE = [-0.4(3) + 0.6(2)] \Delta_{o} + 0PE\)
\(= [0] \Delta_{o}\)
e. Ti+3
d1 so there is no possibility of low spin or high spin
Exercise 2.9.2:
a) Δo < PE, so high-spin.
b) Δo > PE, so high-spin.
c) Δo > PE, so high-spin.
Exercise 2.9.3:
high-spin d6
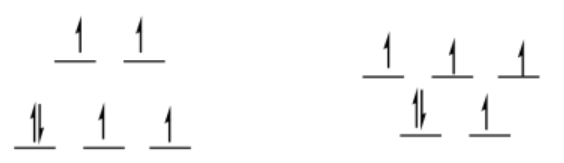
octahedral
\[SE = [2(0.6) -4(0.4)] \Delta_{o} + PE \nonumber\]
\[SE = -0.4 \Delta_{o} + PE \nonumber\]
tetrahedral
\[SE = [3(0.4) - 3(0.6)] \frac{4}{9} \Delta_{o} + PE \nonumber\]
\[SE = -0.6 \Delta_{o} + PE \nonumber\]
\[\Delta SE = SE_{oh} - SE_{td} = -0.4 \Delta_{o} + PE -(-0.6 \Delta_{o} + PE\) = +0.2 \Delta_{o} \nonumber\]
This is a slight preference for tetrahedral.
low-spin d6
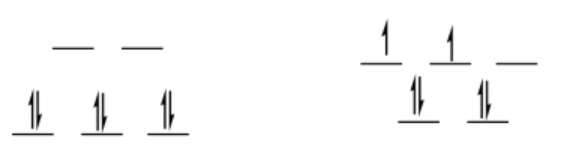
octahedral
\[SE = [0(0.6) -6(0.4)] \Delta_{o} + 3PE \nonumber\]
\[SE = -2.4\Delta_{o} + 3PE \nonumber\]
tetrahedral
\[SE = [2(0.4) -4(0.6)] \frac{4}{9} \Delta_{o} + 2PE \nonumber\]
\[SE = -1.6 \Delta_{o} + PE \nonumber\]
\[\Delta SE = SE_{oh} -SE_{td} = -2.4 \Delta_{o} + 3PE -(-1.6 \Delta_{o} + 2PE) = -0.8 \Delta_{o} + PE \nonumber\]
This is a preference for octahedral, although it would be offset by the pairing energy
Exercise 2.9.4:
high-spin d8

square planar
\[SE = [1.23 + 0.23 -2(0.43) -4(0.51)]\Delta_{o} + 3PE \nonumber\]
\[SE = -1.44 \Delta_{o} + 3PE \nonumber\]
tetrahedral
\[SE = [4(0.4) -4(0.6)] \frac{4}{9} \Delta_{o} + 3PE \nonumber\]
\[SE = -0.36 \Delta_{o} + 3PE \nonumber\]
\[\Delta SE = SE_{sq} - SE_{td} = -1.44 \Delta_{o} + 3PE -(-0.36 \Delta_{o} + 3PE) = -1.08 \Delta_{o} \nonumber\]
This is an appreciable preference for square planar.
low-spin d8
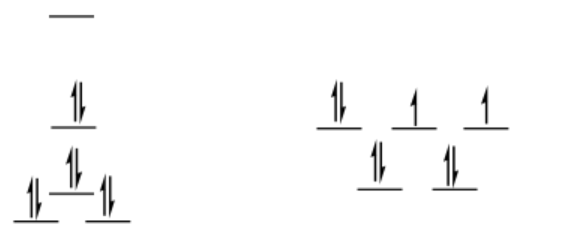
square planar
\[SE = [0 + 2(0.23) -2 (0.43) -4 (0.51)]\Delta_{o} + 4PE \nonumber\]
\[SE = -2.44 \Delta _{O} + 4PE \nonumber\]
tetrahedral = same as before (ls = hs for d8 tetrahedral)
\[\Delta SE = SE_{sq} - SE_{td} = -2.44 \Delta_{O} + 3PE -(-0.36 \Delta _{O} + 3PE) = -2.08 \Delta_{O} + PE \nonumber\]
This is an even more appreciable preference for square planar, although it is offset by pairing energy. Pairing energy would have to be twice as big as Δo in order to completely offet the LFSE.
Exercise 2.10.1:
The weaker donors include halides and oxygen donors. Nitrogen atom donors are mostly a little stronger than that. The strongest donors include carbon donors, especially with pi bonds.
Exercise 2.10.2:
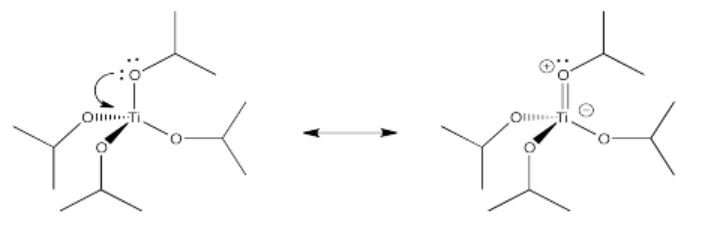
Exercise 2.10.3:
Pi donation raises the t2g electrons (the d electrons of proper symmetry for pi overlap with the ligands in an octahedral geometry).
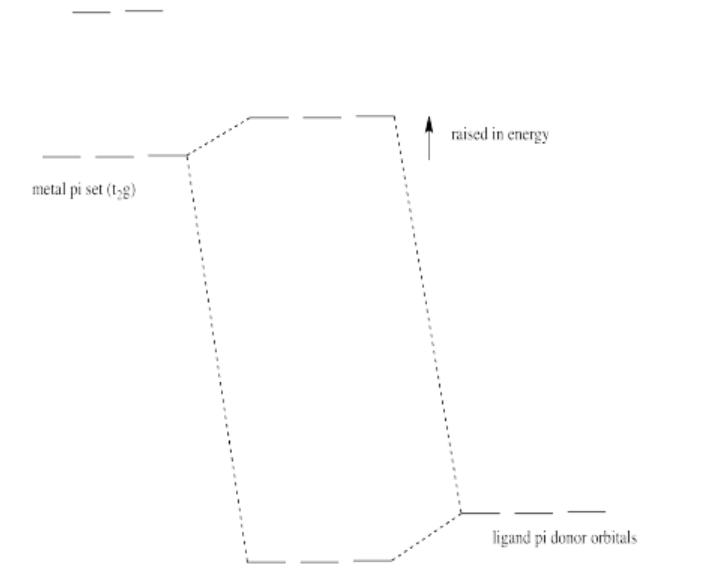
Exercise 2.10.6:
Because chloride is a weaker ligand than hydroxide, the d orbital splitting gets smaller. A d-d transition would involve less energy, so it would move to longer wavelength (red shift).
Exercise 2.10.7:
a) The [Cu(OH2)6]2+ ion appears blue-green, so it absorbs a reddish orange, about 650 nm; whereas the [Cu(NH3)2(OH2)4]2+ ion appears indigo-violet, so it absorbs yellow, about 600 nm.
b) Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon). The [Cu(NH3)2(OH2)4]2+ ion absorbs the shorter wavelength, higher energy photon.
c) The [Cu(NH3)2(OH2)4]2+ ion has the greater d-d gap.
d) The ammonia must be a stronger field ligand than water. In general terms we might think of that as a result of ammonia being only a sigma-donor, whereas water is also a pi-donor.
Exercise 2.10.8:
a) The [Cu(NH3)6]3+ ion appears yellow, so it absorbs violet, about 400 nm; whereas the [Cu(NH3)5Cl]2+ ion appears pink, so it absorbs green, about 550 nm.
b) Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon). The [Cu(NH3)6]3+ ion absorbs the shorter wavelength, higher energy photon.
c) The [Cu(NH3)6]3+ ion has the greater d-d gap.
d) The ammonia must be a stronger field ligand than chloride. In general terms we might think of that as a result of ammonia being only a sigma-donor, whereas chloride is also a pi-donor.
Exercise 2.10.9:
The green compound absorbs red; the violet compound absorbs yellow; the yellow compound absorbs violet.
In terms of energy these absorbances can be ranked:
(high energy) violet photon > yellow photon > red photon (low energy)
or in terms of d-d gap:
large gap > middle gap > small gap
In the spectrochemical series, we would expect the order of corresponding ligands to be:
-CN > H2O > F-
The cyano compound absorbs violet and appears yellow; the aquo compound absorbs yellow and appears violet; the fluoro compound absords red and appears green.
Exercise 2.10.10:
a) The [V(OH2)6]3+ ion appears yellow, so it absorbs violet, about 400 nm; whereas the [V(OH2)6]2+ ion appears pink, so it absorbs green, about 550 nm.
b) Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon). The [V(OH2)6]3+ ion absorbs the shorter wavelength, higher energy photon.
c) The [V(OH2)6]3+ ion has the greater d-d gap.
d) One ion contains V3+, whereas the other ion contains V2+. As charge increases on an ion, electrons contract toward the nucleus. However, low-lying electrons, which are closer to the nucleus to begin with, are attracted even more than are high-lying electrons. thus, as charge increases on the ion, the d-d splitting increases.
Exercise 2.10.11:
a) [Co(NH3)6]+3
The metal is +3 suggesting a large Δ0
The ligands are sigma donors, so medium field ligands
The splitting energy is large thus low spin.
b) [Fe(CN)6]-4
The metal is first row, +2 suggesting intermediate Δ0
The ligands are pi acceptors, so strong field ligands
The splitting energy is large thus low spin.
c) [CoF6]-4
The metal is first row, +2 suggesting a large Δ0
The ligands are pi donors, so weak field ligands
The splitting energy is small thus high spin.
d) [Rh(CN)6]-3
The metal is 2nd row (4d) and +3 suggesting a large Δ0
The ligands are pi acceptors, so strong field ligands
The splitting energy is large thus low spin.
e) [V(OH2)6]+3
The complex is d2, so there is only one possible spin state.
f) [Fe(py)6]+2
The metal is first row, +2 suggesting intermediate Δ0
The ligands are pi acceptors, so strong field ligands
The splitting energy is large thus low spin.
g) [MnCl6]-4
The metal is first row, +2 suggesting intermediate Δ0
The ligands are pi donors, so weak field ligands
The splitting energy is large thus high spin.
h) [Ru(NH3)6]+2
The metal is 2nd row (4d) and +2 suggesting a large Δ0
The ligands are sigma donors, so medium field ligands
The splitting energy is large thus low spin.
Exercise 2.11.1:
a) The ions in LiF are both smaller than in KBr, so the force of attraction between the ions in LiF is greater because of the smaller separation between the charges.
b) Calcium has a 2+ charge in CaCl2, whereas potassium has only a + charge, so the chloride ions are more strongly attracted to the calcium than to the potassium.
Problem CC11.3.
a) labile (electrons in higher energy d orbital set)
b) not labile (all electrons in lower energy d orbitals)
c) not labile (all electrons in lower energy d orbitals)
d) labile (electrons in higher energy d orbital set)
e) labile (electrons in higher energy d orbital set)
Exercise 2.12.1:
a) yes; ls d7 is eg1, so one level has one electron and the other has none - net decrease in energy upon distortion
b) no; d8 is eg2, so both levels have one electron -- no net change in energy upon distortion
Exercise 2.12.2:
a) Co2+ yes; d7 so eg1
b) Ag2+ yes; d9 so eg3
c) Ni2+ no; d8 so eg2
d) Mn2+ no if hs; d5 so eg2. However, if it were low-spin (unlikely with a first-row metal in a moderately low oxidation state and π-donors), then there would be degeneracy and distortion.
e) Ag+ no; d10 so eg4
Exercise 2.12.3:
a) [V(CN)6]3- yes d2 t2g2 b) [Cr(CN)6]3- no d3 t2g3
c) [Mn(CN)6]3- yes d4 t2g4 d) [Fe(CN)6]3- yes d5 t2g5
e) [Cr(CN)6]4- yes d4 t2g4 f) [Mn(CN)6]4- yes d5 t2g5
g) [Fe(CN)6]4- no d6 t2g6


