2.14: Solutions to Selected Problems
- Page ID
- 195682
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise 2.1.1:
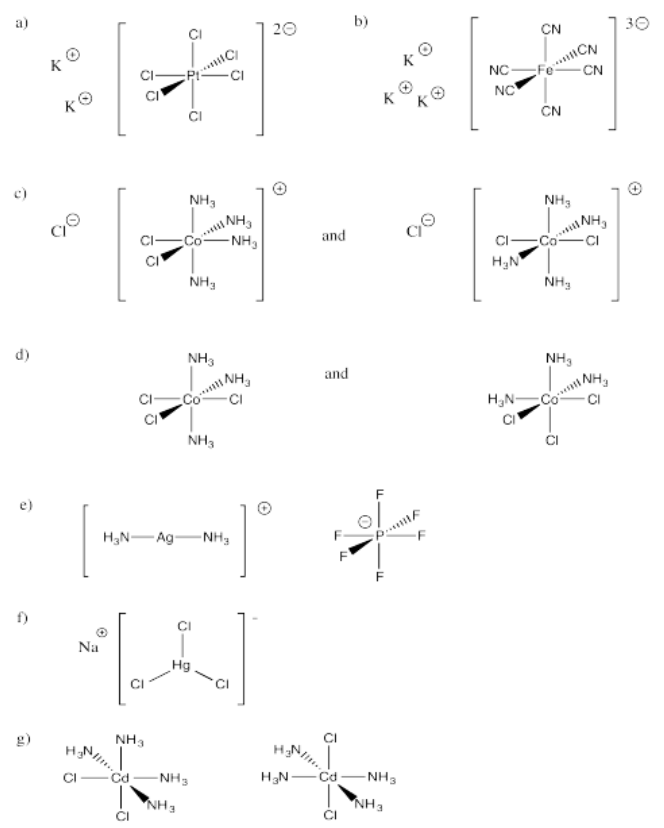

Exercise 2.2.1:
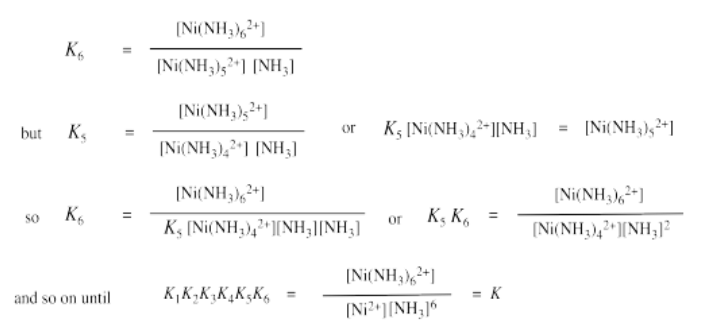
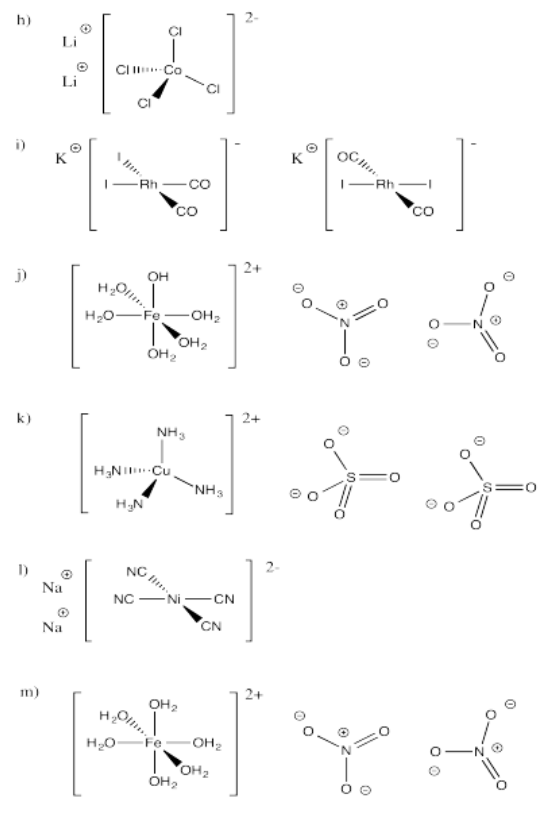
Exercise 2.2.2:
a) \(K = K_{1} \times K_{2} \times K_{3} \times K_{4} \times K_{5} \times K_{6}\)
= \(470 \times 130 \times 41 \times 12 \times 4.2 \times 0.81\)
=\(1.03 \times 10^{8}\)
b) As the nickel binds ammonia ligands, it becomes more electronically saturated. That means it becomes less Lewis acidic. It does not have as strong an attraction for additional ligands.
Exercise 2.2.3:
- This is a Zn2+ ion binding to either NH3 or CN- ligands. The zinc cation is more strongly sttracted to the anionic cyanide ligands than the neutral ammonia ligand, so the binding constant with cyanide is higher than with ammonia.
- Both cases involve cyanide ions. In one case, the CN- binds to Fe2+, whereas the other case involves Fe3+. The ligand is more attracted to the more highly charged ion, so the binding constant is higher.
Exercise 2.3.4:
a) Metal valence count: 9
Metal with charge: 6
Donated by ligands: 6 x 2 = 12
Total: 18
b) Metal valence count: 8
Metal with charge: 5
Donated by ligands: 6 x 2 = 12
Total: 17
c) Metal valence count: 9
Metal with charge: 7
Donated by ligands: 6 x 2 = 12
Total: 19
d) Metal valence count: 7
Metal with charge: 0
Donated by ligands: 4 x 4 = 16
Total: 16
e) Metal valence count: 8
Metal with charge: 8
Donated by ligands: 5 x 2 = 10
Total: 18
f) Metal valence count: 10
Metal with charge: 6
Donated by ligands: 6 x 2 = 12
Total: 18
g) Metal valence count: 6
Metal with charge: 6
Donated by ligands: 6 x 2 = 12
Total: 18
h) Metal valence count: 6
Metal with charge: 0
Donated by ligands: 4 x 4 = 16
Total: 16
i) Metal valence count: 9
Metal with charge: 8
Donated by ligands: 4 x 2 = 8
Total: 16
j) Metal valence count: 8
Metal with charge: 4
Donated by ligands: 3 x 4 = 12
Total: 16
k) Metal valence count: 9
Metal with charge: 7
Donated by ligands: 4 x 2 = 8
Total: 15
Exercise 2.3.5:
a) 6 b) 8 c) 5 d) 5 e) 10 f) 1 g) 10 h) 12 i) 2 j) 9 k) 4
a) Metal valence count: 5
Metal with charge: 0
Donated by ligands: 5 x 2 = 10
Total: 10
b) Metal valence count: 8
Metal with charge: 5
Donated by ligands: 3 x 2 = 6
Total: 11
c) Metal valence count: 6
Metal with charge: 0
Donated by ligands: 6 x 2 = 12
Total: 12
Exercise 2.3.8:
- PF3 (104 vs 870)
- PMe3 (118 vs 870)
- PtBu3 (182 vs 1180)
- PtBu3 (182 vs 1450)
Exercise 2.4.1:
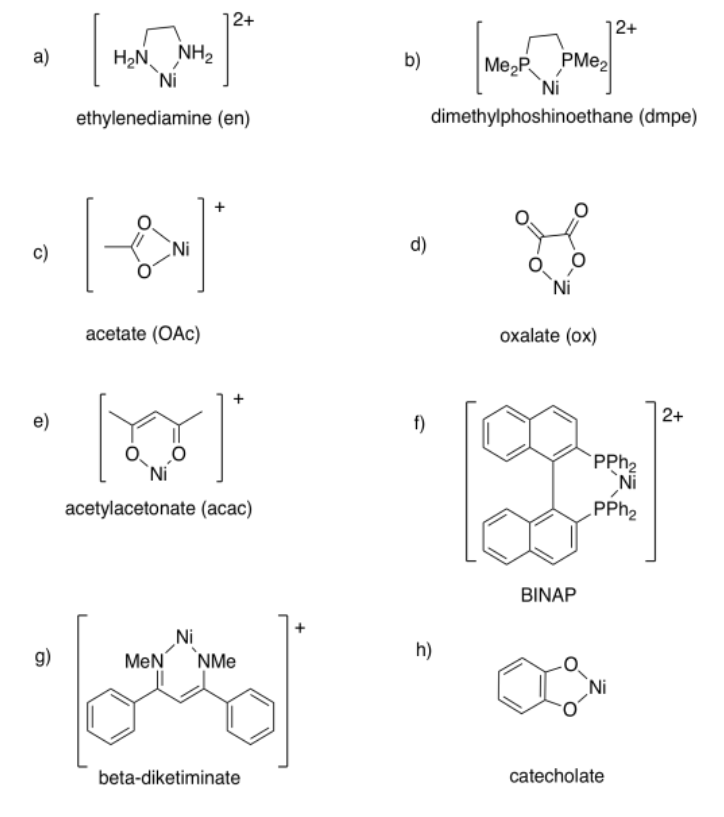
Exercise 2.4.2:
- tridentate or κ3; ligand = 0; metal = 1+
- bidentate or κ2; ligand = 1-; metal = 0
- bidentate or κ2; ligand = 0; metal = 2+
- tetradentate or κ4; ligand = 2-; metal = 2+
- tridentate or κ3; ligand = 0; metal = 1+
- bidentate or κ2; ligand = 0; metal = 1+
Exercise 2.4.3:
- monodentate or κ1; maximum bidentate or κ2; ligand = 0; metal = 2+
- bidentate or κ2; maximum tridentate or κ3; ligand = 1-; metal = 1+
- bidentate or κ2; maximum tridentate or κ3; ligand = 0; metal = 1+
- bidentate or κ2; maximum tetradentate or κ4; ligand = 0; metal = 2+
- tridentate or κ3; maximum tetradentate or κ4; ligand = 1-; metal = 2+
- tridentate or κ3; maximum tetradentate or κ4; ligand = 2-; metal = 2+
Exercise 2.4.4:
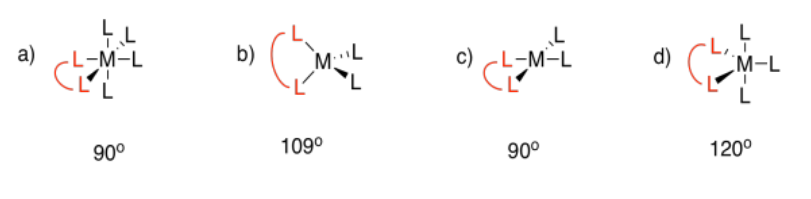
Exercise 2.4.5:
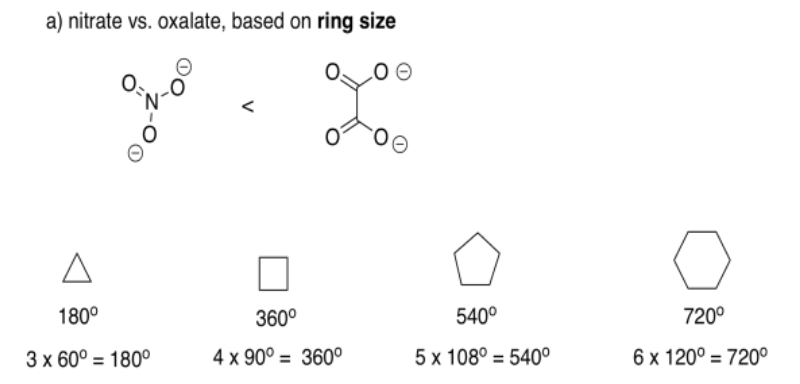
The total of the interior angles of a regular polyhedron is given by (n-2)180o, in which n is the number of sides in the polyhedron. Assuming the ring formed by the bidentate ligand and the metal is a regular polyhedron (it won't be, but we are simplifying), then nitrate gives a triangle with 60° angles, including a 60° O-M-O bite angle. Oxalate gives a square with a larger, 90° bite angle.
In reality, the bite angle for nitrate varies with the complex that is formed, but it is usually somewhere around sixty degrees, whereas oxalate usually gives somewhere around eighty five degrees (see, for example, Alvarez, Chem. Rev. 2015, 115, 13447-13483). The smaller ring size gives a smaller bite angle.
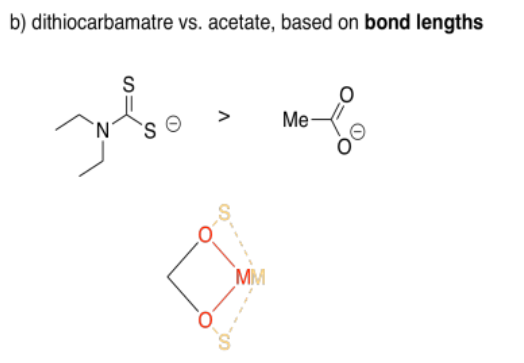
Sulfur is larger than oxygen, so its bonds will be a little longer. As a result, you can imagine those two sides of the square being a little longer with sulfur than with oxygen. From the perspective of the metal, the gap between the two donor atoms widens out a little.
Acetate forms bite angles of around sixty degrees, but dithiocarbamate forms larger bite angles of seventy or seventy five degrees.
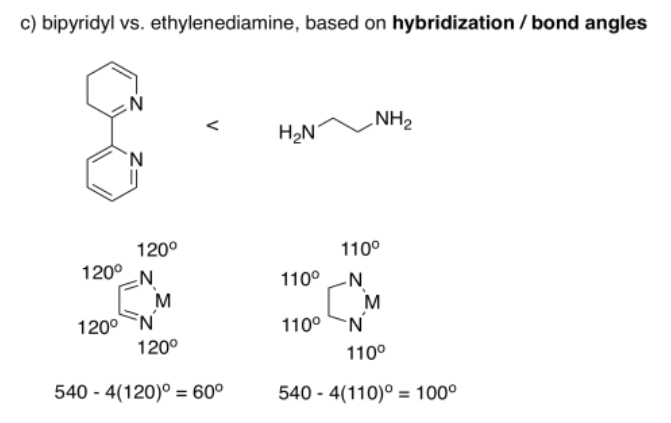
There are lots of differences between these two ligands, but if we simplify and only consider bond angle, we can make a prediction. If the atoms in bipridyl can be considered sp2 hybridised, then they form 120° bond angles. The atoms in ethylenediamine could be considered sp3 hybridised, forming approximately 110° angles. The angle N-M-N still has to complete the shape of the regular pentagon, so if all of the other angles are bigger in the bipyridyl complex, we would expect the bite angle to be smaller.
Really, the bite angles are much closer than this rough estimate suggests. Bipyridyl forms average bite angles of around eighty degrees, whereas ethylenediamine forms average bite angles of around eighty-five degrees. Keep in mind that those are just averages, though. These two values are close enough that their ranges overlap; lots of bipyridyl complexes would have bite angles smaller than ethylenediamine complexes.
Exercise 2.4.6:
Exercise 2.5.1:
Exercise 2.5.2:
Exercise 2.5.3:
Exercise 2.5.4:

Exercise 2.5.5:
Exercise 2.5.6:
Zr(IV) or Zr4+ has no valence d electrons. That means that, although an alkene could certainly donate its pi bond to the zirconium atom, the zirconium has no electrons with which it can stabilize the alkene complex via "back-donation" to the pi antibonding orbital on the alkene.
Nevertheless, d0 metals such as Zr(IV) and Ti(IV) can be used as alkene polymerization catalysts to make common plastics such as HDPE, LDPE and polypropylene. That means that, although an alkene complex isn't directly observed with these metal ions, these metals can evidently bind alkenes briefly and get them to react with other alkenes to form long chains. Even so, most industrial olefin polymerization catalysts use Ti(III).
Exercise 2.5.8:
We will use (a), the binding constant between Ag(I) and ethylene or ethene (CH2=CH2), as our baseline value. Other constants will be compared with this one in order to look for a trend.
In (b), the binding constant is much smaller, so the silver ion binds cis-2-hexene much less tightly than it does ethene. This is just another alkene, like ethene, but instead of having just hydrogen atoms attached to the C=C unit, cis-2-hexene has some other stuff. Maybe this other stuff causes some problem for alkene binding. The obvious difference between hydrogen atoms and this other stuff is that this other stuff is bigger. Maybe the complex gets too crowded when the cis-2-hexene binds to the silver ion.
Very often when we see metal ions on paper, we are not dealing with bare metal ions in reality. The ion often has other ligands already attached to it at the beginning, such as water molecules, and what we are sometimes looking at is replacement of an old ligand with a new ligand. Other ligands attached to the silver could make crowding problems even worse.
There is an alternative explanation as well. If you compare two alkenes that differ only in the number of hydrogens attached to the double bond, such as 1-butene, CH2=CHCH2CH3, and 2-butene, CH3CH=CHCH3, you invariably find that the alkene with fewer hydrogens attached to the double bond (and more other stuff) is more stable. "Terminal alkenes", with double bonds at the ends of the chain, are always less stable than "internal alkenes", with double bonds somewhere along the middle of the chain. This difference can be explained by looking at some quantum mechanical calculations, but we're not going to do that right now.
The point is, the difference in this reaction might be caused, not by the alkene complexes, but by the alkenes themselves, on the other side of the reaction profile. It's important to remember that equilibrium constants always compare two sides of a reaction. Ethene, having fewer substituents on the double bond than cis-2-hexene ("substituents" is a four syllable word for "other stuff"), may simply be less stable and more reactive.
Do either of these ideas hold up in the other examples?
In (c), trans-2-hexene is bound even less tightly than cis-2-hexene. We could argue that in a cis-2-hexene complex, the substituents, which are on the same side of the double bond, might both be held away from other ligands on the metal that may exacerbate crowding problems. That would be more difficult to do with trans-2-hexene, since one substituent is on either side of the double bond. Getting one substituent away from the crowding may be possible, but probably not both.
Once again, the alternative explanation holds up here, too. cis-2-Hexene is less stable than trans-2-hexene, because the substituents on the double bond crowd each other in cis-2-hexene, but are held away from each other in trans-2-hexene. So maybe cis-2-hexene binds to silver ion more easily because it is more reactive.
Exercise 2.6.1:
- There are two double bonds here, and they are conjugated: CH2=CH-CH=CH2. The conjugated double bond would allow the ligand to bind η4.
- There are two double bonds here, but they are not conjugated: CH2=CH-CH2-CH=CH2. Each double bond would bind η2, and the ligand would be able to bind in a bidentate fashion, but since the double bonds are not conjugated and binding all in a row, we would not describe binding as η4. It would most commonly be described as η2,η2; that simply means each double bond is an η2-donor, and there are two of them. It could also be considered a κ2 donor because of its denticity.
- This is another non-conjugated case: CH2=CH-CH2-CH2-CH=CH2. In terms of hapticity, it could be described as η2,η2.
- There are three double bonds here, and they are conjugated: CH2=CH-CH=CH-CH=CH2. The conjugated double bond would allow the ligand to bind η6.
Exercise 2.6.2:
- The ligand is bound η5; it donates 6 electrons, from two double bonds and one lone pair; the ligand has a charge of -1.
- The ligand is bound η4; it donates 4 electrons, from two double bonds; the ligand has no charge.
- The ligand is bound η7; it donates 8 electrons, from three double bonds and one lone pair; the ligand has a charge of -1.
- The ligand is bound η6; it donates 6 electrons, from three double bonds; the ligand has no charge.
Exercise 2.6.3
- The ligand is bound η1; it donates one lone pair; however, it could donate an additional pi bond and then it would bind η3.
- The ligand is bound η2; it donates one pi bond; however, it could donate two more pi bonds and then it would bind η6.
- The ligand is bound η4; it donates two pi bonds; however, it could donate one more pi bond and then it would bind η6.
- The ligand is bound η3; it donates one lone pair and one pi bond; however, it could donate an additional pi bond and then it would bind η5.
- The ligand is bound η4; it donates two pi bonds; however, it could donate one more pi bond and then it would bind η6.
- The ligand is bound η2; it donates one pi bond; however, it could donate one more pi bond and then it would bind η4.
Exercise 2.6.4:
- The resulting anion has aromatic stability. It is cyclic, fully conjugated, flat and has an odd number of electron pairs.
- Cp anion could bind to a metal through just one pair or through two pairs, but in most cases it will bind via three pairs of electrons.
d) Valence count on metal: 8
Count on metal, correcting for +2 charge: 6
Donated from ligands: 2 x 6 = 12
Total: 18
Exercise 2.6.5:
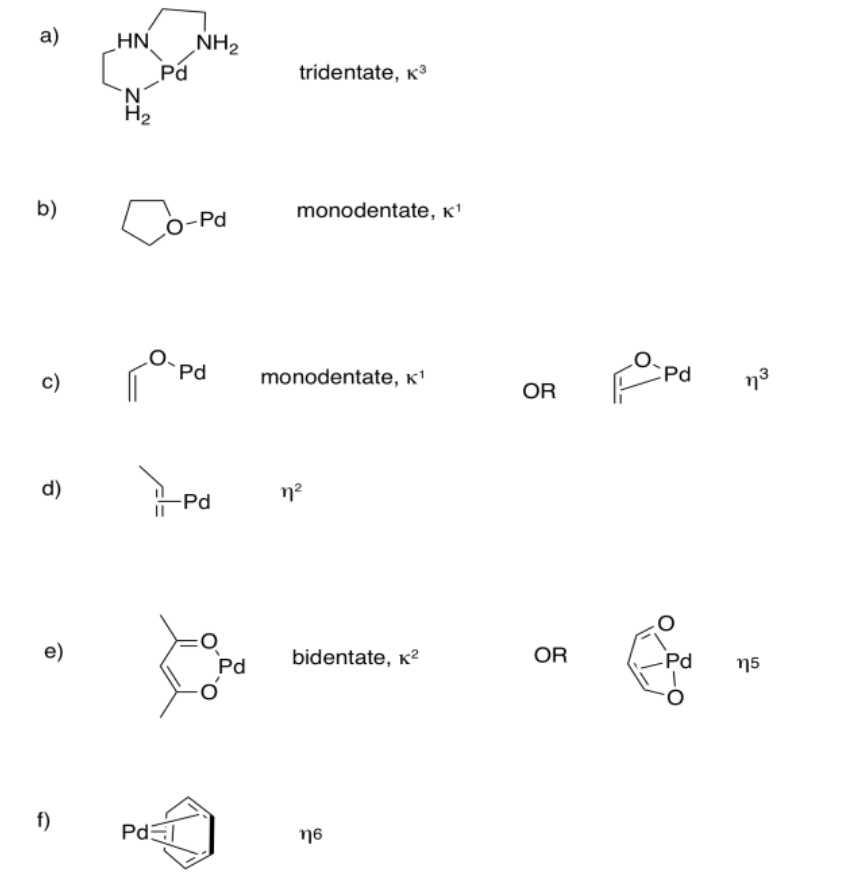
Exercise 2.6.6:
This problem deals with the "bite angle" of the ligand. Remember, a chain of atoms becomes more flexible the longer it gets, because of the possibility for rotation around each bond along the chain. As the two double bonds move further apart from each other (one bond apart in (a), two bonds apart in (b) and three bonds apart in (c)), the chain can "open up" and bind with a more optimal overlap with the metal.


