2.4: Chelation

Monodentate ligands bind through only one donor atom. Monodentate means "one-toothed". The halides, phosphines, ammonia and amines seen previously are monodentate ligands.

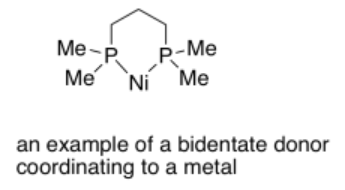
Bidentate ligands bind through two donor sites. Bidentate means "two-toothed". An example of a bidentate ligand is bis(dimethylphosphino)propane. It can bind to a metal via two donor atoms at once: it uses one lone pair on each phosphorus atom.

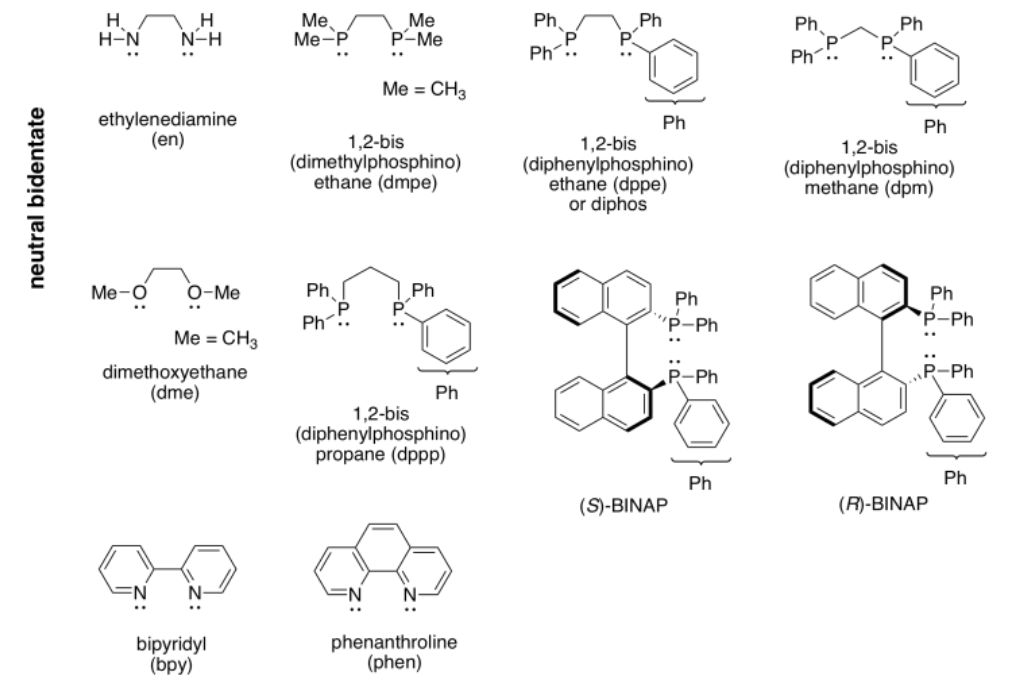
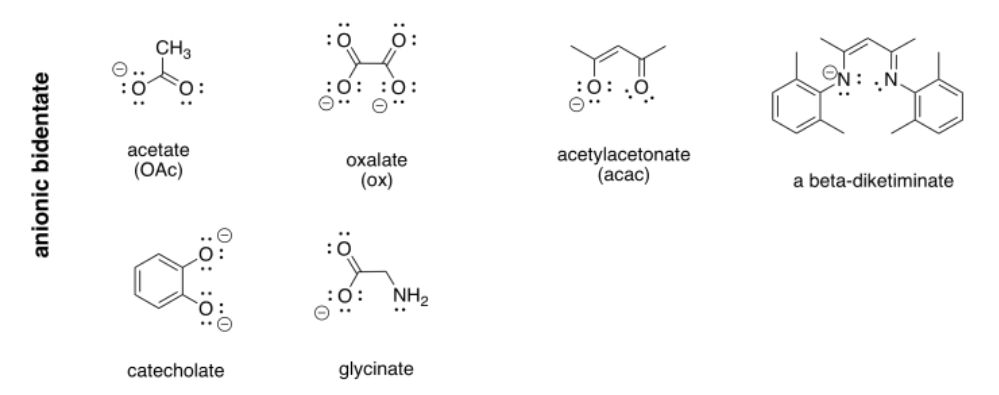
More examples of bidentate ligands are shown below. They all have at least two different atoms with lone pairs. In some cases, there are additional atoms with lone pairs, but only two of them are able to face the metal at one time. Oxalate and glycinate would act as bidentate donors, donating up to two sets of lone pairs at the same time.

Table CC \(\PageIndex{1}\) Some common bidentate ligands

Bidentate binding allows a ligand to bind more tightly. Tridentate ligands, which bind through three donors, can bind even more tightly, and so on. This phenomenon is generally called the "chelate effect". This term comes from the Greek chelos, meaning "crab". A crab does not have any teeth at all, but it does have two claws for tightly holding onto something.for a couple of reasons. A very simple analogy is that, if you are holding something with two hands rather than one, you are not as likely to drop it.

• Multidentate ligands bind more tightly because of the chelate effect

The chemical reasons for the chelate effect involve relative enthalpy and entropy changes upon binding a multidentate ligand. In terms of enthalpy, in order to completely remove a bidentate ligand, two coordinate bonds must be broken. That costs more energy than breaking one coordinate bond for a monodentate ligand.

In terms of entropy, which deals with the distribution of energy within a system, it is generally thought that bringing two molecules together (a bidentate ligand and a metal complex) costs less than bringing three molecules together (two monodentate ligands and a metal complex). That's because individual molecules are free to move around, tumble and vibrate independently. Once they come together, they have to do all these things together. Since these different types of motion represent different ways of distributing energy, if the system becomes more restricted, energy can't be distributed in as many states.

• Energy is lowered even more by two bonding interactions
• Compared to two separate donors, bidentate donation is entropically favored

Exercise \(\PageIndex{1}\)

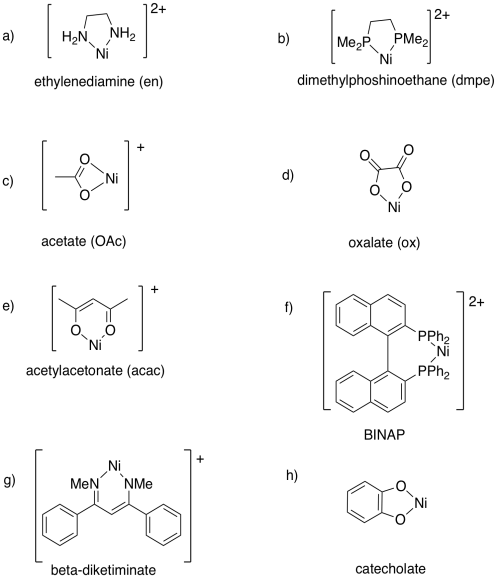
Draw metal complexes using the ligands below, binding to Ni(2+) in a bidentate mode.

Answer

A ligand could be monodentate, meaning it binds through a lone pair on a single atom. It could be bidentate, meaning it binds through lone pairs on two different atoms. It could even be tridentate, with three atoms bearing their own lone pairs, tetradentate, and so on.

Table CC \(\PageIndex{2}\) Examples of polydentate ligands.

There is a symbol for denticity, κ (it's a Greek letter, pronounced "kappa"), which simply describes how many atoms are bound to the metal. For example, in ethylenediamine or 1,2-diaminoethane, NH₂CH₂CH₂NH₂, the two nitrogen atoms can be bound to the metal at the same time, although none of the other atoms in between would be directly attached to the metal. This donor is capable of binding in a κ² mode. However, if for some reason one of the nitrogen atoms lets go of the metal so that the ethylenediamine is hanging on by only one nitrogen, we would say that the ligand is binding in κ¹ mode.

Exercise \(\PageIndex{2}\)

In each of the following cases,

i) describe the denticity;

ii) indicate the charge on the ligand and on the metal.

Answer

Answer a

tridentate or κ³; ligand = 0; metal = 1+

Answer b

bidentate or κ²; ligand = 1-; metal = 0

Answer c

bidentate or κ²; ligand = 0; metal = 2+

Answer d

tetradentate or κ⁴; ligand = 2-; metal = 2+

Answer e

tridentate or κ³; ligand = 0; metal = 1+

Answer f

bidentate or κ²; ligand = 0; metal = 1+

Exercise \(\PageIndex{3}\)

In the following cases, the ligand has slipped, so that it isn't binding as tightly as it possibly could. In each case,

i) describe the denticity as drawn;

ii) state the maximum denticity possible;

iii) indicate the charge on the ligand and on the metal

Answer

Answer a

monodentate or κ¹; maximum bidentate or κ²; ligand = 0; metal = 2+

Answer b

bidentate or κ²; maximum tridentate or κ³; ligand = 1-; metal = 1+

Answer c

bidentate or κ²; maximum tridentate or κ³; ligand = 0; metal = 1+

Answer d

bidentate or κ²; maximum tetradentate or κ⁴; ligand = 0; metal = 2+

Answer e

tridentate or κ³; maximum tetradentate or κ⁴; ligand = 1-; metal = 2+

Answer f

tridentate or κ³; maximum tetradentate or κ⁴; ligand = 2-; metal = 2+

There are more subtle aspects of chelation. For example, two different bidentate ligands may not necessarily bind to the metal in exactly the same way. In the drawing below, it's apparent that the three bidentate phosphine ligands, bis(dimethylphosphino)methane, bis(dimethylphosphino)ethane, and bis(dimethylphosphino)propane, do not all bind the metal with the same geometry. In each case, the metal forms a different angle with the two phosphines.

The term "bite angle" is frequently used to describe how different bidentate ligands will attach to metals at different angles. In the picture, the P-Pd-P angle appears to be about 90 degrees when dmpm is bound; in reality it is even smaller. With dmpe, the bite angle appears larger in the picture than the one for dmpm, and in reality it is larger, although not quite as large as it appears here. Two different ligands that bind with two different bite angles will have different influences on the complex that forms. In fact, chemists often use these differences to "tune" the behavior of transition metals that are used as catalysts for important properties. They might add similar ligands with different bite angles to see which one best promotes the desired catalytic reaction.

Many factors can influence the bite angle, including structural features of the bidentate ligand itself, the metal, and other ligands bound to the metal. However, a particular ligand will usually have a normal range of bite angles that it will be able to adopt under different circumstances.

Exercise \(\PageIndex{4}\)

Certain ligands may have natural bite angles that work better in some cases than in others. Propose the optimum bite angle in each of the following geometries.

Answer

Exercise \(\PageIndex{5}\)

Certain ligands tend to give a certain range of bite angles. Use the suggested criterion to predict which ligand in each pair would give the larger bite angle.

Answer

Answer a

The total of the interior angles of a regular polyhedron is given by (n-2)180^o, in which n is the number of sides in the polyhedron. Assuming the ring formed by the bidentate ligand and the metal is a regular polyhedron (it won't be, but we are simplifying), then nitrate gives a triangle with 60° angles, including a 60° O-M-O bite angle. Oxalate gives a square with a larger, 90° bite angle.

In reality, the bite angle for nitrate varies with the complex that is formed, but it is usually somewhere around sixty degrees, whereas oxalate usually gives somewhere around eighty five degrees (see, for example, Alvarez, Chem. Rev. 2015, 115, 13447-13483). The smaller ring size gives a smaller bite angle.

Answer b

Sulfur is larger than oxygen, so its bonds will be a little longer. As a result, you can imagine those two sides of the square being a little longer with sulfur than with oxygen. From the perspective of the metal, the gap between the two donor atoms widens out a little.

Acetate forms bite angles of around sixty degrees, but dithiocarbamate forms larger bite angles of seventy or seventy five degrees.

Answer c

There are lots of differences between these two ligands, but if we simplify and only consider bond angle, we can make a prediction. If the atoms in bipridyl can be considered sp² hybridised, then they form 120° bond angles. The atoms in ethylenediamine could be considered sp³ hybridised, forming approximately 110° angles. The angle N-M-N still has to complete the shape of the regular pentagon, so if all of the other angles are bigger in the bipyridyl complex, we would expect the bite angle to be smaller.

Really, the bite angles are much closer than this rough estimate suggests. Bipyridyl forms average bite angles of around eighty degrees, whereas ethylenediamine forms average bite angles of around eighty-five degrees. Keep in mind that those are just averages, though. These two values are close enough that their ranges overlap; lots of bipyridyl complexes would have bite angles smaller than ethylenediamine complexes.

Exercise \(\PageIndex{6}\)

Suggest which ligand in each pair would have the larger bite angle, and why.

Answer