11.2: Intermolecular forces
- Page ID
- 349557
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Explain the following laws within the Ideal Gas Law
The properties of liquids are intermediate between those of gases and solids but are more similar to solids. In contrast to intramolecular forces, such as the covalent bonds that hold atoms together in molecules and polyatomic ions, intermolecular forces hold molecules together in a liquid or solid. Intermolecular forces are generally much weaker than covalent bonds. For example, it requires 927 kJ to overcome the intramolecular forces and break both O–H bonds in 1 mol of water, but it takes only about 41 kJ to overcome the intermolecular attractions and convert 1 mol of liquid water to water vapor at 100°C. (Despite this seemingly low value, the intermolecular forces in liquid water are among the strongest such forces known!) Given the large difference in the strengths of intra- and intermolecular forces, changes between the solid, liquid, and gaseous states almost invariably occur for molecular substances without breaking covalent bonds.
Note the Pattern
The properties of liquids are intermediate between those of gases and solids but are more similar to solids.
Intermolecular forces determine bulk properties such as the melting points of solids and the boiling points of liquids. Liquids boil when the molecules have enough thermal energy to overcome the intermolecular attractive forces that hold them together, thereby forming bubbles of vapor within the liquid. Similarly, solids melt when the molecules acquire enough thermal energy to overcome the intermolecular forces that lock them into place in the solid.
Intermolecular forces are electrostatic in nature; that is, they arise from the interaction between positively and negatively charged species. Like covalent and ionic bonds, intermolecular interactions are the sum of both attractive and repulsive components. Because electrostatic interactions fall off rapidly with increasing distance between molecules, intermolecular interactions are most important for solids and liquids, where the molecules are close together. These interactions become important for gases only at very high pressures, where they are responsible for the observed deviations from the ideal gas law at high pressures. (For more information on the behavior of real gases and deviations from the ideal gas law, see Section 7.1.)
In this section, we explicitly consider three kinds of intermolecular interactions:There are two additional types of electrostatic interaction that you are already familiar with: the ion–ion interactions that are responsible for ionic bonding and the ion–dipole interactions that occur when ionic substances dissolve in a polar substance such as water. (For more information on ionic bonding, see Chapter 4. For more information on the dissolution of ionic substances, see Chapter 9) dipole–dipole interactions, London dispersion forces, and hydrogen bonds. The first two are often described collectively as van der Waals forcesThe intermolecular forces known as dipole–dipole interactions and London dispersion forces..
Dipole–Dipole Interactions
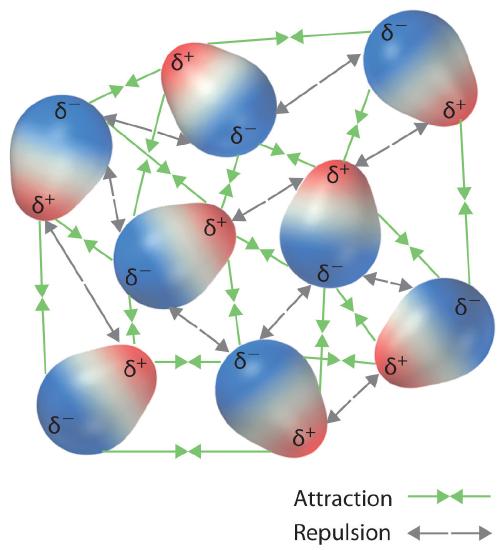
Recall from Chapter 4 that polar covalent bonds behave as if the bonded atoms have localized fractional charges that are equal but opposite (i.e., the two bonded atoms generate a dipole). If the structure of a molecule is such that the individual bond dipoles do not cancel one another, then the molecule has a net dipole moment. Molecules with net dipole moments tend to align themselves so that the positive end of one dipole is near the negative end of another and vice versa, as shown in part (a) in Figure 11.2.1 . These arrangements are more stable than arrangements in which two positive or two negative ends are adjacent (part (c) in Figure 11.2.1). Hence dipole–dipole interactionsA kind of intermolecular interaction (force) that results between molecules with net dipole moments., such as those in part (b) in Figure 11.2.1 , are attractive intermolecular interactions, whereas those in part (d) in Figure 11.2.1 are repulsive intermolecular interactions. Because molecules in a liquid move freely and continuously, molecules always experience both attractive and repulsive dipole–dipole interactions simultaneously, as shown in Figure 11.2.2 . On average, however, the attractive interactions dominate.
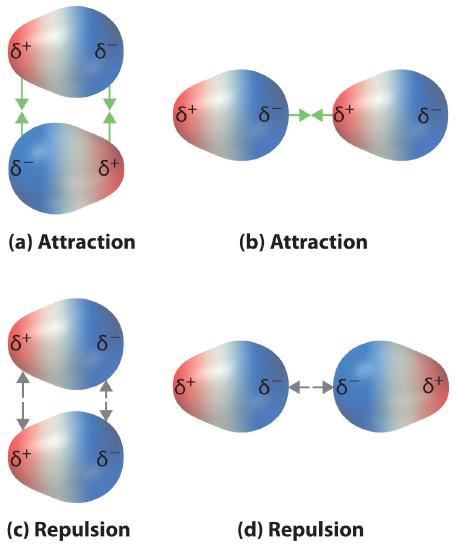
Figure 11.2.2 Both Attractive and Repulsive Dipole–Dipole Interactions Occur in a Liquid Sample with Many Molecules
Because each end of a dipole possesses only a fraction of the charge of an electron, dipole–dipole interactions are substantially weaker than the interactions between two ions, each of which has a charge of at least ±1, or between a dipole and an ion, in which one of the species has at least a full positive or negative charge. In addition, the attractive interaction between dipoles falls off much more rapidly with increasing distance than do the ion–ion interactions we considered in Chapter 4 . Recall that the attractive energy between two ions is proportional to 1/r, where r is the distance between the ions. Doubling the distance (r → 2r) decreases the attractive energy by one-half. In contrast, the energy of the interaction of two dipoles is proportional to 1/r6, so doubling the distance between the dipoles decreases the strength of the interaction by 26, or 64-fold. Thus a substance such as HCl, which is partially held together by dipole–dipole interactions, is a gas at room temperature and 1 atm pressure, whereas NaCl, which is held together by interionic interactions, is a high-melting-point solid. Within a series of compounds of similar molar mass, the strength of the intermolecular interactions increases as the dipole moment of the molecules increases, as shown in Table 11.2.1 . Using what we learned in Chapter 5 about predicting relative bond polarities from the electronegativities of the bonded atoms, we can make educated guesses about the relative boiling points of similar molecules.
Table 11.2.1 Relationships between the Dipole Moment and the Boiling Point for Organic Compounds of Similar Molar Mass
| Compound | Molar Mass (g/mol) | Dipole Moment (D) | Boiling Point (K) |
|---|---|---|---|
| C3H6 (cyclopropane) | 42 | 0 | 240 |
| CH3OCH3 (dimethyl ether) | 46 | 1.30 | 248 |
| CH3CN (acetonitrile) | 41 | 3.9 | 355 |
Note the Pattern
The attractive energy between two ions is proportional to 1/r, whereas the attractive energy between two dipoles is proportional to 1/r6.
Example 11.2.1
Arrange ethyl methyl ether (CH3OCH2CH3), 2-methylpropane [isobutane, (CH3)2CHCH3], and acetone (CH3COCH3) in order of increasing boiling points. Their structures are as follows:
Given: compounds
Asked for: order of increasing boiling points
Strategy:
Compare the molar masses and the polarities of the compounds. Compounds with higher molar masses and that are polar will have the highest boiling points.
Solution:
The three compounds have essentially the same molar mass (58–60 g/mol), so we must look at differences in polarity to predict the strength of the intermolecular dipole–dipole interactions and thus the boiling points of the compounds. The first compound, 2-methylpropane, contains only C–H bonds, which are not very polar because C and H have similar electronegativities. It should therefore have a very small (but nonzero) dipole moment and a very low boiling point. Ethyl methyl ether has a structure similar to H2O; it contains two polar C–O single bonds oriented at about a 109° angle to each other, in addition to relatively nonpolar C–H bonds. As a result, the C–O bond dipoles partially reinforce one another and generate a significant dipole moment that should give a moderately high boiling point. Acetone contains a polar C=O double bond oriented at about 120° to two methyl groups with nonpolar C–H bonds. The C–O bond dipole therefore corresponds to the molecular dipole, which should result in both a rather large dipole moment and a high boiling point. Thus we predict the following order of boiling points: 2-methylpropane < ethyl methyl ether < acetone. This result is in good agreement with the actual data: 2-methylpropane, boiling point = −11.7°C, and the dipole moment (μ) = 0.13 D; methyl ethyl ether, boiling point = 7.4°C and μ = 1.17 D; acetone, boiling point = 56.1°C and μ = 2.88 D.
Exercise
Arrange carbon tetrafluoride (CF4), ethyl methyl sulfide (CH3SC2H5), dimethyl sulfoxide [(CH3)2S=O], and 2-methylbutane [isopentane, (CH3)2CHCH2CH3] in order of decreasing boiling points.
Answer: dimethyl sulfoxide (boiling point = 189.9°C) > ethyl methyl sulfide (boiling point = 67°C) > 2-methylbutane (boiling point = 27.8°C) > carbon tetrafluoride (boiling point = −128°C)
London Dispersion Forces
Thus far we have considered only interactions between polar molecules, but other factors must be considered to explain why many nonpolar molecules, such as bromine, benzene, and hexane, are liquids at room temperature, and others, such as iodine and naphthalene, are solids. Even the noble gases can be liquefied or solidified at low temperatures, high pressures, or both (Table 11.2.2 )
What kind of attractive forces can exist between nonpolar molecules or atoms? This question was answered by Fritz London (1900–1954), a German physicist who later worked in the United States. In 1930, London proposed that temporary fluctuations in the electron distributions within atoms and nonpolar molecules could result in the formation of short-lived instantaneous dipole momentsThe short-lived dipole moment in atoms and nonpolar molecules caused by the constant motion of their electrons, which results in an asymmetrical distribution of charge at any given instant., which produce attractive forces called London dispersion forcesA kind of intermolecular interaction (force) that results from temporary fluctuations in the electron distribution within atoms and nonpolar molecules. between otherwise nonpolar substances.

Table 11.2.2 Normal Melting and Boiling Points of Some Elements and Nonpolar Compounds
| Substance | Molar Mass (g/mol) | Melting Point (°C) | Boiling Point (°C) |
|---|---|---|---|
| Ar | 40 | −189.4 | −185.9 |
| Xe | 131 | −111.8 | −108.1 |
| N2 | 28 | −210 | −195.8 |
| O2 | 32 | −218.8 | −183.0 |
| F2 | 38 | −219.7 | −188.1 |
| I2 | 254 | 113.7 | 184.4 |
| CH4 | 16 | −182.5 | −161.5 |
Consider a pair of adjacent He atoms, for example. On average, the two electrons in each He atom are uniformly distributed around the nucleus. Because the electrons are in constant motion, however, their distribution in one atom is likely to be asymmetrical at any given instant, resulting in an instantaneous dipole moment. As shown in part (a) in Figure 11.2.3, the instantaneous dipole moment on one atom can interact with the electrons in an adjacent atom, pulling them toward the positive end of the instantaneous dipole or repelling them from the negative end. The net effect is that the first atom causes the temporary formation of a dipole, called an induced dipoleA short-lived dipole moment that is created in atoms and nonpolar molecules adjacent to atoms or molecules with an instantaneous dipole moment., in the second. Interactions between these temporary dipoles cause atoms to be attracted to one another. These attractive interactions are weak and fall off rapidly with increasing distance. London was able to show with quantum mechanics that the attractive energy between molecules due to temporary dipole–induced dipole interactions falls off as 1/r6. Doubling the distance therefore decreases the attractive energy by 26, or 64-fold.
Instantaneous dipole–induced dipole interactions between nonpolar molecules can produce intermolecular attractions just as they produce interatomic attractions in monatomic substances like Xe. This effect, illustrated for two H2 molecules in part (b) in Figure 11.2.3 tends to become more pronounced as atomic and molecular masses increase (Table 11.2.2 ). For example, Xe boils at −108.1°C, whereas He boils at −269°C. The reason for this trend is that the strength of London dispersion forces is related to the ease with which the electron distribution in a given atom can be perturbed. In small atoms such as He, the two 1s electrons are held close to the nucleus in a very small volume, and electron–electron repulsions are strong enough to prevent significant asymmetry in their distribution. In larger atoms such as Xe, however, the outer electrons are much less strongly attracted to the nucleus because of filled intervening shells. (For more information on shielding, see Section 2.2) As a result, it is relatively easy to temporarily deform the electron distribution to generate an instantaneous or induced dipole. The ease of deformation of the electron distribution in an atom or molecule is called its polarizabilityThe ease of deformation of the electron distribution in an atom or molecule.. Because the electron distribution is more easily perturbed in large, heavy species than in small, light species, we say that heavier substances tend to be much more polarizable than lighter ones.
Note the Pattern
For similar substances, London dispersion forces get stronger with increasing molecular size.
The polarizability of a substance also determines how it interacts with ions and species that possess permanent dipoles, as we shall see when we discuss solutions in Chapter 13. Thus London dispersion forces are responsible for the general trend toward higher boiling points with increased molecular mass and greater surface area in a homologous series of compounds, such as the alkanes (part (a) in Figure 11.2.4 ). The strengths of London dispersion forces also depend significantly on molecular shape because shape determines how much of one molecule can interact with its neighboring molecules at any given time. For example, part (b) in Figure 11.2.4 shows 2,2-dimethylpropane (neopentane) and n-pentane, both of which have the empirical formula C5H12. Neopentane is almost spherical, with a small surface area for intermolecular interactions, whereas n-pentane has an extended conformation that enables it to come into close contact with other n-pentane molecules. As a result, the boiling point of neopentane (9.5°C) is more than 25°C lower than the boiling point of n-pentane (36.1°C).
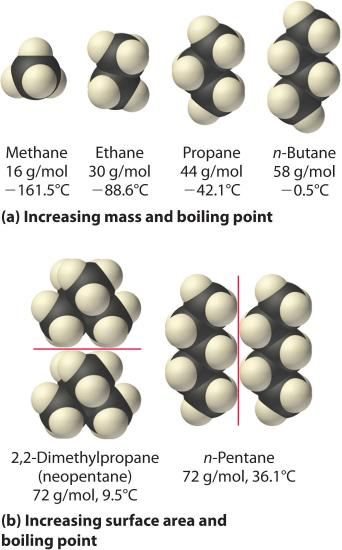
All molecules, whether polar or nonpolar, are attracted to one another by London dispersion forces in addition to any other attractive forces that may be present. In general, however, dipole–dipole interactions in small polar molecules are significantly stronger than London dispersion forces, so the former predominate.
Example 11.2.2
Arrange n-butane, propane, 2-methylpropane [isobutene, (CH3)2CHCH3], and n-pentane in order of increasing boiling points.
Given: compounds
Asked for: order of increasing boiling points
Strategy:
Determine the intermolecular forces in the compounds and then arrange the compounds according to the strength of those forces. The substance with the weakest forces will have the lowest boiling point.
Solution:
The four compounds are alkanes and nonpolar, so London dispersion forces are the only important intermolecular forces. These forces are generally stronger with increasing molecular mass, so propane should have the lowest boiling point and n-pentane should have the highest, with the two butane isomers falling in between. Of the two butane isomers, 2-methylpropane is more compact, and n-butane has the more extended shape. Consequently, we expect intermolecular interactions for n-butane to be stronger due to its larger surface area, resulting in a higher boiling point. The overall order is thus as follows, with actual boiling points in parentheses: propane (−42.1°C) < 2-methylpropane (−11.7°C) < n-butane (−0.5°C) < n-pentane (36.1°C).
Exercise
Arrange GeH4, SiCl4, SiH4, CH4, and GeCl4 in order of decreasing boiling points.
Answer: GeCl4 (87°C) > SiCl4 (57.6°C) > GeH4 (−88.5°C) > SiH4 (−111.8°C) > CH4 (−161°C)
Hydrogen Bonds
Molecules with hydrogen atoms bonded to electronegative atoms such as O, N, and F (and to a much lesser extent Cl and S) tend to exhibit unusually strong intermolecular interactions. These result in much higher boiling points than are observed for substances in which London dispersion forces dominate, as illustrated for the covalent hydrides of elements of groups 14–17 in Figure 11.2.5 . Methane and its heavier congeners in group 14 form a series whose boiling points increase smoothly with increasing molar mass. This is the expected trend in nonpolar molecules, for which London dispersion forces are the exclusive intermolecular forces. In contrast, the hydrides of the lightest members of groups 15–17 have boiling points that are more than 100°C greater than predicted on the basis of their molar masses. The effect is most dramatic for water: if we extend the straight line connecting the points for H2Te and H2Se to the line for period 2, we obtain an estimated boiling point of −130°C for water! Imagine the implications for life on Earth if water boiled at −130°C rather than 100°C.
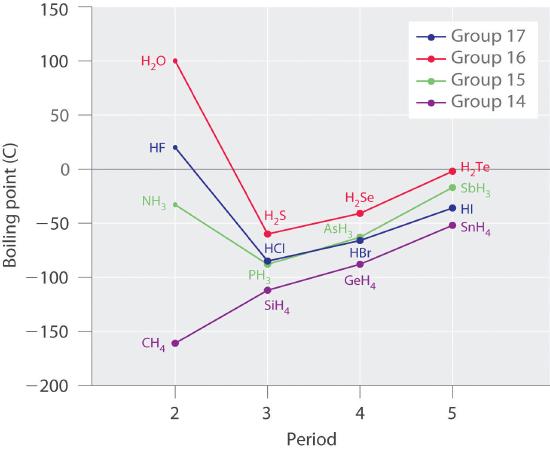
Why do strong intermolecular forces produce such anomalously high boiling points and other unusual properties, such as high enthalpies of vaporization and high melting points? The answer lies in the highly polar nature of the bonds between hydrogen and very electronegative elements such as O, N, and F. The large difference in electronegativity results in a large partial positive charge on hydrogen and a correspondingly large partial negative charge on the O, N, or F atom. Consequently, H–O, H–N, and H–F bonds have very large bond dipoles that can interact strongly with one another. Because a hydrogen atom is so small, these dipoles can also approach one another more closely than most other dipoles. The combination of large bond dipoles and short dipole–dipole distances results in very strong dipole–dipole interactions called hydrogen bondsAn unusually strong dipole-dipole interaction (intermolecular force) that results when hydrogen is bonded to very electronegative elements, such as O, N, and F., as shown for ice in Figure 11.2.6 . A hydrogen bond is usually indicated by a dotted line between the hydrogen atom attached to O, N, or F (the hydrogen bond donor) and the atom that has the lone pair of electrons (the hydrogen bond acceptor). Because each water molecule contains two hydrogen atoms and two lone pairs, a tetrahedral arrangement maximizes the number of hydrogen bonds that can be formed. In the structure of ice, each oxygen atom is surrounded by a distorted tetrahedron of hydrogen atoms that form bridges to the oxygen atoms of adjacent water molecules. The bridging hydrogen atoms are not equidistant from the two oxygen atoms they connect, however. Instead, each hydrogen atom is 101 pm from one oxygen and 174 pm from the other. In contrast, each oxygen atom is bonded to two H atoms at the shorter distance and two at the longer distance, corresponding to two O–H covalent bonds and two O⋅H hydrogen bonds from adjacent water molecules, respectively. The resulting open, cagelike structure of ice means that the solid is actually slightly less dense than the liquid, which explains why ice floats on water rather than sinks.
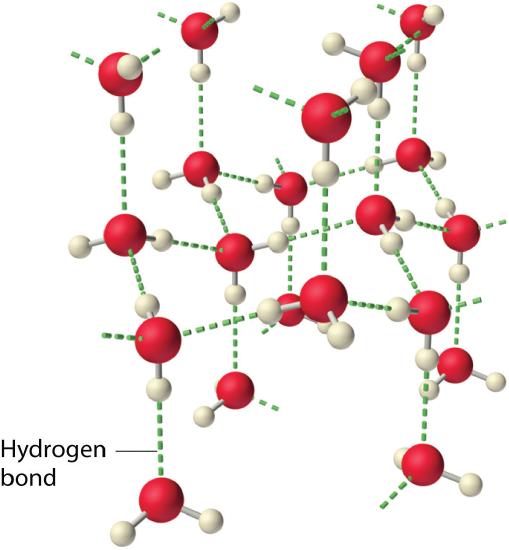
Note the Pattern
Hydrogen bond formation requires both a hydrogen bond donor and a hydrogen bond acceptor.
Because ice is less dense than liquid water, rivers, lakes, and oceans freeze from the top down. In fact, the ice forms a protective surface layer that insulates the rest of the water, allowing fish and other organisms to survive in the lower levels of a frozen lake or sea. If ice were denser than the liquid, the ice formed at the surface in cold weather would sink as fast as it formed. Bodies of water would freeze from the bottom up, which would be lethal for most aquatic creatures. The expansion of water when freezing also explains why automobile or boat engines must be protected by “antifreeze” (we will discuss how antifreeze works in Chapter 13) and why unprotected pipes in houses break if they are allowed to freeze.
Although hydrogen bonds are significantly weaker than covalent bonds, with typical dissociation energies of only 15–25 kJ/mol, they have a significant influence on the physical properties of a compound. Compounds such as HF can form only two hydrogen bonds at a time as can, on average, pure liquid NH3. Consequently, even though their molecular masses are similar to that of water, their boiling points are significantly lower than the boiling point of water, which forms four hydrogen bonds at a time.
Example 11.2.3
Considering CH3OH, C2H6, Xe, and (CH3)3N, which can form hydrogen bonds with themselves? Draw the hydrogen-bonded structures.
Given: compounds
Asked for: formation of hydrogen bonds and structure
Strategy:
A Identify the compounds with a hydrogen atom attached to O, N, or F. These are likely to be able to act as hydrogen bond donors.
B Of the compounds that can act as hydrogen bond donors, identify those that also contain lone pairs of electrons, which allow them to be hydrogen bond acceptors. If a substance is both a hydrogen donor and a hydrogen bond acceptor, draw a structure showing the hydrogen bonding.
Solution:
A Of the species listed, xenon (Xe), ethane (C2H6), and trimethylamine [(CH3)3N] do not contain a hydrogen atom attached to O, N, or F; hence they cannot act as hydrogen bond donors.
B The one compound that can act as a hydrogen bond donor, methanol (CH3OH), contains both a hydrogen atom attached to O (making it a hydrogen bond donor) and two lone pairs of electrons on O (making it a hydrogen bond acceptor); methanol can thus form hydrogen bonds by acting as either a hydrogen bond donor or a hydrogen bond acceptor. The hydrogen-bonded structure of methanol is as follows:
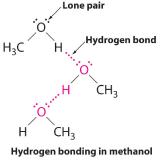
Exercise
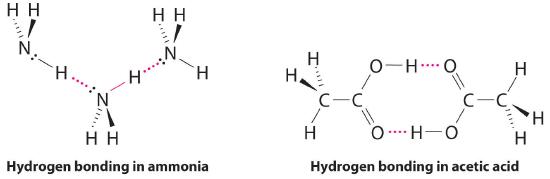
Considering CH3CO2H, (CH3)3N, NH3, and CH3F, which can form hydrogen bonds with themselves? Draw the hydrogen-bonded structures.
Answer: CH3CO2H and NH3;
Example 11.2.4
Arrange C60 (buckminsterfullerene, which has a cage structure), NaCl, He, Ar, and N2O in order of increasing boiling points.
Given: compounds
Asked for: order of increasing boiling points
Strategy:
Identify the intermolecular forces in each compound and then arrange the compounds according to the strength of those forces. The substance with the weakest forces will have the lowest boiling point.
Solution:
Electrostatic interactions are strongest for an ionic compound, so we expect NaCl to have the highest boiling point. To predict the relative boiling points of the other compounds, we must consider their polarity (for dipole–dipole interactions), their ability to form hydrogen bonds, and their molar mass (for London dispersion forces). Helium is nonpolar and by far the lightest, so it should have the lowest boiling point. Argon and N2O have very similar molar masses (40 and 44 g/mol, respectively), but N2O is polar while Ar is not. Consequently, N2O should have a higher boiling point. A C60 molecule is nonpolar, but its molar mass is 720 g/mol, much greater than that of Ar or N2O. Because the boiling points of nonpolar substances increase rapidly with molecular mass, C60 should boil at a higher temperature than the other nonionic substances. The predicted order is thus as follows, with actual boiling points in parentheses: He (−269°C) < Ar (−185.7°C) < N2O (−88.5°C) < C60 (>280°C) < NaCl (1465°C).
Exercise
Arrange 2,4-dimethylheptane, Ne, CS2, Cl2, and KBr in order of decreasing boiling points.
Answer: KBr (1435°C) > 2,4-dimethylheptane (132.9°C) > CS2 (46.6°C) > Cl2 (−34.6°C) > Ne (−246°C)
Summary
Molecules in liquids are held to other molecules by intermolecular interactions, which are weaker than the intramolecular interactions that hold the atoms together within molecules and polyatomic ions. Transitions between the solid and liquid or the liquid and gas phases are due to changes in intermolecular interactions but do not affect intramolecular interactions. The three major types of intermolecular interactions are dipole–dipole interactions, London dispersion forces (these two are often referred to collectively as van der Waals forces), and hydrogen bonds. Dipole–dipole interactions arise from the electrostatic interactions of the positive and negative ends of molecules with permanent dipole moments; their strength is proportional to the magnitude of the dipole moment and to 1/r6, where r is the distance between dipoles. London dispersion forces are due to the formation of instantaneous dipole moments in polar or nonpolar molecules as a result of short-lived fluctuations of electron charge distribution, which in turn cause the temporary formation of an induced dipole in adjacent molecules. Like dipole–dipole interactions, their energy falls off as 1/r6. Larger atoms tend to be more polarizable than smaller ones because their outer electrons are less tightly bound and are therefore more easily perturbed. Hydrogen bonds are especially strong dipole–dipole interactions between molecules that have hydrogen bonded to a highly electronegative atom, such as O, N, or F. The resulting partially positively charged H atom on one molecule (the hydrogen bond donor) can interact strongly with a lone pair of electrons of a partially negatively charged O, N, or F atom on adjacent molecules (the hydrogen bond acceptor). Because of strong O⋅H> hydrogen bonding between water molecules, water has an unusually high boiling point, and ice has an open, cagelike structure that is less dense than liquid water.
Key Takeaway
- Intermolecular forces are electrostatic in nature and include van der Waals forces and hydrogen bonds.
Conceptual Problems
-
What is the main difference between intramolecular interactions and intermolecular interactions? Which is typically stronger? How are changes of state affected by these different kinds of interactions?
-
Describe the three major kinds of intermolecular interactions discussed in this chapter and their major features. The hydrogen bond is actually an example of one of the other two types of interaction. Identify the kind of interaction that includes hydrogen bonds and explain why hydrogen bonds fall into this category.
-
Which are stronger—dipole–dipole interactions or London dispersion forces? Which are likely to be more important in a molecule with heavy atoms? Explain your answers.
-
Explain why hydrogen bonds are unusually strong compared to other dipole–dipole interactions. How does the strength of hydrogen bonds compare with the strength of covalent bonds?
-
Liquid water is essential for life as we know it, but based on its molecular mass, water should be a gas under standard conditions. Why is water a liquid rather than a gas under standard conditions?
-
Describe the effect of polarity, molecular mass, and hydrogen bonding on the melting point and boiling point of a substance.
-
Why are intermolecular interactions more important for liquids and solids than for gases? Under what conditions must these interactions be considered for gases?
-
Using acetic acid as an example, illustrate both attractive and repulsive intermolecular interactions. How does the boiling point of a substance depend on the magnitude of the repulsive intermolecular interactions?
-
In group 17, elemental fluorine and chlorine are gases, whereas bromine is a liquid and iodine is a solid. Why?
-
The boiling points of the anhydrous hydrogen halides are as follows: HF, 19°C; HCl, −85°C; HBr, −67°C; and HI, −34°C. Explain any trends in the data, as well as any deviations from that trend.
-
Identify the most important intermolecular interaction in each of the following.
- SO2
- HF
- CO2
- CCl4
- CH2Cl2
-
Identify the most important intermolecular interaction in each of the following.
- LiF
- I2
- ICl
- NH3
- NH2Cl
-
Would you expect London dispersion forces to be more important for Xe or Ne? Why? (The atomic radius of Ne is 38 pm, whereas that of Xe is 108 pm.)
-
Arrange Kr, Cl2, H2, N2, Ne, and O2 in order of increasing polarizability. Explain your reasoning.
-
Both water and methanol have anomalously high boiling points due to hydrogen bonding, but the boiling point of water is greater than that of methanol despite its lower molecular mass. Why? Draw the structures of these two compounds, including any lone pairs, and indicate potential hydrogen bonds.
-
The structures of ethanol, ethylene glycol, and glycerin are as follows:

Arrange these compounds in order of increasing boiling point. Explain your rationale.
-
Do you expect the boiling point of H2S to be higher or lower than that of H2O? Justify your answer.
-
Ammonia (NH3), methylamine (CH3NH2), and ethylamine (CH3CH2NH2) are gases at room temperature, while propylamine (CH3CH2CH2NH2) is a liquid at room temperature. Explain these observations.
-
Why is it not advisable to freeze a sealed glass bottle that is completely filled with water? Use both macroscopic and microscopic models to explain your answer. Is a similar consideration required for a bottle containing pure ethanol? Why or why not?
-
Which compound in the following pairs will have the higher boiling point? Explain your reasoning.
- NH3 or PH3
- ethylene glycol (HOCH2CH2OH) or ethanol
- 2,2-dimethylpropanol [CH3C(CH3)2CH2OH] or n-butanol (CH3CH2CH2CH2OH)
-
Some recipes call for vigorous boiling, while others call for gentle simmering. What is the difference in the temperature of the cooking liquid between boiling and simmering? What is the difference in energy input?
-
Use the melting of a metal such as lead to explain the process of melting in terms of what is happening at the molecular level. As a piece of lead melts, the temperature of the metal remains constant, even though energy is being added continuously. Why?
-
How does the O–H distance in a hydrogen bond in liquid water compare with the O–H distance in the covalent O–H bond in the H2O molecule? What effect does this have on the structure and density of ice?
-
- Explain why the hydrogen bonds in liquid HF are stronger than the corresponding intermolecular <math display="inline" xml:id="av_1.0-ch11_m003"><semantics><mrow><mtext>H</mtext><mo>⋅</mo><mo>⋅</mo><mo>⋅</mo><mtext>I</mtext></mrow></semantics></math> interactions in liquid HI.
- In which substance are the individual hydrogen bonds stronger: HF or H2O? Explain your reasoning.
- For which substance will hydrogen bonding have the greater effect on the boiling point: HF or H2O? Explain your reasoning.
Answers
-
Water is a liquid under standard conditions because of its unique ability to form four strong hydrogen bonds per molecule.
-
As the atomic mass of the halogens increases, so does the number of electrons and the average distance of those electrons from the nucleus. Larger atoms with more electrons are more easily polarized than smaller atoms, and the increase in polarizability with atomic number increases the strength of London dispersion forces. These intermolecular interactions are strong enough to favor the condensed states for bromine and iodine under normal conditions of temperature and pressure.
-
- The V-shaped SO2 molecule has a large dipole moment due to the polar S=O bonds, so dipole–dipole interactions will be most important.
- The H–F bond is highly polar, and the fluorine atom has three lone pairs of electrons to act as hydrogen bond acceptors; hydrogen bonding will be most important.
- Although the C=O bonds are polar, this linear molecule has no net dipole moment; hence, London dispersion forces are most important.
- This is a symmetrical molecule that has no net dipole moment, and the Cl atoms are relatively polarizable; thus, London dispersion forces will dominate.
- This molecule has a small dipole moment, as well as polarizable Cl atoms. In such a case, dipole–dipole interactions and London dispersion forces are often comparable in magnitude.
-
Water has two polar O–H bonds with H atoms that can act as hydrogen bond donors, plus two lone pairs of electrons that can act as hydrogen bond acceptors, giving a net of four hydrogen bonds per H2O molecule. Although methanol also has two lone pairs of electrons on oxygen that can act as hydrogen bond acceptors, it only has one O–H bond with an H atom that can act as a hydrogen bond donor. Consequently, methanol can only form two hydrogen bonds per molecule on average, versus four for water. Hydrogen bonding therefore has a much greater effect on the boiling point of water.
-
Vigorous boiling causes more water molecule to escape into the vapor phase, but does not affect the temperature of the liquid. Vigorous boiling requires a higher energy input than does gentle simmering.
Contributors
- Anonymous
Modified by Joshua Halpern, Scott Sinex and Scott Johnson