5.2: Enthalpy and Reactions
- Page ID
- 349706
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To know the key features of a state function.
- To understand why enthalpy is an important state function.
To study the flow of energy during a chemical reaction, we need to distinguish between a systemThe small, well-defined part of the universe in which we are interested., the small, well-defined part of the universe in which we are interested (such as a chemical reaction), and its surroundingsAll the universe that is not the system; that is, system + surroundings = universe., the rest of the universe, including the container in which the reaction is carried out (Figure \(\PageIndex{1}\) ). In the discussion that follows, the mixture of chemical substances that undergoes a reaction is always the system, and the flow of heat can be from the system to the surroundings or vice versa.
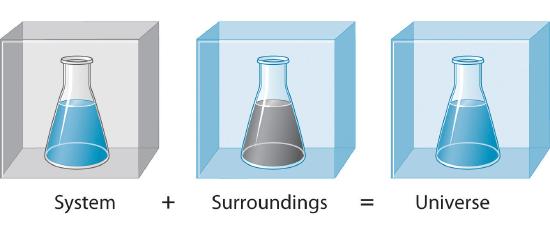
Figure \(\PageIndex{1}\) A System and Its Surroundings The system is that part of the universe we are interested in studying, such as a chemical reaction inside a flask. The surroundings are the rest of the universe, including the container in which the reaction is carried out.
Three kinds of systems are important in chemistry. An open systemA system that can exchange both matter and energy with its surroundings. can exchange both matter and energy with its surroundings. A pot of boiling water is an open system because a burner supplies energy in the form of heat, and matter in the form of water vapor is lost as the water boils. A closed systemA system that can exchange energy but not matter with its surroundings. can exchange energy but not matter with its surroundings. The sealed pouch of a ready-made dinner that is dropped into a pot of boiling water is a closed system because thermal energy is transferred to the system from the boiling water but no matter is exchanged (unless the pouch leaks, in which case it is no longer a closed system). An isolated systemA system that can exchange neither energy nor matter with its suroundings. exchanges neither energy nor matter with the surroundings. Energy is always exchanged between a system and its surroundings, although this process may take place very slowly. A truly isolated system does not actually exist. An insulated thermos containing hot coffee approximates an isolated system, but eventually the coffee cools as heat is transferred to the surroundings. In all cases, the amount of heat lost by a system is equal to the amount of heat gained by its surroundings and vice versa. That is, the total energy of a system plus its surroundings is constant, which must be true if energy is conserved.
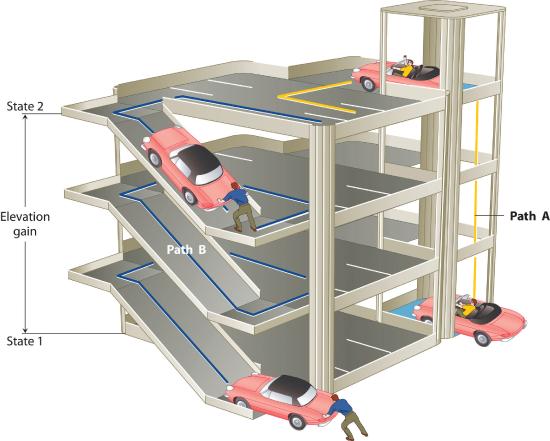
The state of a systemA complete description of the system at a given time, including its temperature and pressure, the amount of matter it contains, its chemical composition, and the physical state of the matter. is a complete description of a system at a given time, including its temperature and pressure, the amount of matter it contains, its chemical composition, and the physical state of the matter. A state functionA property of a system whose magnitude depends on only the present state of the system, not its previous history. is a property of a system whose magnitude depends on only the present state of the system, not its previous history. Temperature, pressure, volume, and potential energy are all state functions. The temperature of an oven, for example, is independent of however many steps it may have taken for it to reach that temperature. Similarly, the pressure in a tire is independent of how often air is pumped into the tire for it to reach that pressure, as is the final volume of air in the tire. Heat and work, on the other hand, are not state functions because they are path dependent. For example, a car sitting on the top level of a parking garage has the same potential energy whether it was lifted by a crane, set there by a helicopter, driven up, or pushed up by a group of students (Figure \(\PageIndex{2}\) ). The amount of work expended to get it there, however, can differ greatly depending on the path chosen. If the students decided to carry the car to the top of the ramp, they would perform a great deal more work than if they simply pushed the car up the ramp (unless, of course, they neglected to release the parking brake, in which case the work expended would increase substantially!). The potential energy of the car is the same, however, no matter which path they choose.
Direction of Heat Flow
The reaction of powdered aluminum with iron(III) oxide, known as the thermite reaction, generates an enormous amount of heat—enough, in fact, to melt steel (see chapter opening image). The balanced chemical equation for the reaction is as follows:
\[ 2Al(s)+Fe_{2}O_{3}(s) \rightarrow 2Fe(s)+Al_{2}O_{3}(s) \]
We can also write this chemical equation as
\[ 2Al(s)+Fe_{2}O_{3}(s) \rightarrow 2Fe(s)+Al_{2}O_{3}(s)+ heat \]
to indicate that heat is one of the products. Chemical equations in which heat is shown as either a reactant or a product are called thermochemical equations. In this reaction, the system consists of aluminum, iron, and oxygen atoms; everything else, including the container, makes up the surroundings. During the reaction, so much heat is produced that the iron liquefies. Eventually, the system cools; the iron solidifies as heat is transferred to the surroundings. A process in which heat (q) is transferred from a system to its surroundings is described as exothermicA process in which heat (q) is transferred from a system to its surroundings.. By convention, q < 0 for an exothermic reaction.
When you hold an ice cube in your hand, heat from the surroundings (including your hand) is transferred to the system (the ice), causing the ice to melt and your hand to become cold. We can describe this process by the following thermochemical equation:
\[ heat + H_{2}O\left (s \right ) \rightarrow H_{2}O\left (l \right ) \]
When heat is transferred to a system from its surroundings, the process is endothermicA process in which heat q>0 is transferred to a system from its surroundings.. By convention, q > 0 for an endothermic reaction.
Enthalpy of Reaction
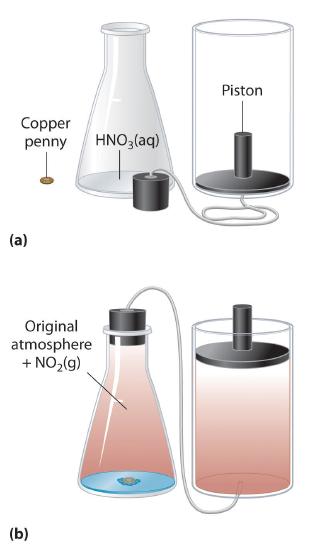
We have stated that the change in energy (ΔE) is equal to the sum of the heat produced and the work performed (Equation 9.1.3). Work done by an expanding gas is called pressure-volume work, also called PV work. Consider, for example, a reaction that produces a gas, such as dissolving a piece of copper in concentrated nitric acid. The chemical equation for this reaction is as follows:
\[ Cu\left (s \right ) + 4HNO_{3}\left (aq \right ) \rightarrow Cu(NO_{3})_{2}\left (aq \right ) + 2H_{2}O\left (l \right ) + 2NO_{3}\left (g \right ) \]
If the reaction is carried out in a closed system that is maintained at constant pressure by a movable piston, the piston will rise as nitrogen dioxide gas is formed (Figure \(\PageIndex{3}\) ). The system is performing work by lifting the piston against the downward force exerted by the atmosphere (i.e., atmospheric pressure). We find the amount of PV work done by multiplying the external pressure P by the change in volume caused by movement of the piston (ΔV). At a constant external pressure (here, atmospheric pressure)
\[ w = -P\Delta V \]
The negative sign associated with PV work done indicates that the system loses energy. If the volume increases at constant pressure (ΔV > 0), the work done by the system is negative, indicating that a system has lost energy by performing work on its surroundings. Conversely, if the volume decreases (ΔV < 0), the work done by the system is positive, which means that the surroundings have performed work on the system, thereby increasing its energy.
The symbol E in Equation \(\PageIndex{3}\) represents the internal energyThe sum of the kinetic and potential energies of all of a system’s component. Internal energy is a state function. of a system, which is the sum of the kinetic energy and potential energy of all its components. Additionally, ΔE = q + w, where q is the heat produced by the system and w is the work performed by the system. It is the change in internal energy that produces heat plus work. Substituting Equation 8.1.5 we find that
\[ \Delta E = q-P \Delta V \]
Thus, if a reaction were carried out in a constant volume system (a pressure cooker for example)
\[ \Delta E = q_{v} \]
Where the subscipt v in qv indicates that the process is carried out at constant volume. Thus, if the volume is held constant, the change in internal energy is equal to the heat flowing into or out of the system. However, we live in a constant pressure world, not a constant volume one. The atmospheric pressure at the surface of the earth where we live is roughly constant allowing for variation in barometric pressure due to weather or altitude.
To measure the energy changes that occur in chemical reactions, chemists usually use a related thermodynamic quantity called enthalpy (H)The sum of a system’s internal energy E and the product of its pressure P and volume V (from the Greek enthalpein, meaning “to warm”). The enthalpy of a system is defined as the sum of its internal energy E plus the product of its pressure P and volume V:
\[ H=E+PV \]
Because internal energy, pressure, and volume are all state functions, enthalpy is also a state function.
If a chemical change occurs at constant pressure (for a given P, ΔP = 0), the change in enthalpy (ΔH)At constant pressure, the amount of heat transferred from the surroundings to the system or ΔH= q is
\[ \Delta H = \Delta (E + PV) = \Delta E + \Delta PV = \Delta E + P\Delta V \]
Substituting q + w for ΔE (Equation \(\PageIndex{9}\) ) and −w for PΔV (Equation \(\PageIndex{5}\) ), we obtain
\[ \Delta H = \Delta E + P\Delta V = q_{p} + w − w = q_{p} \]
The subscript p is used here to emphasize that this equation is true only for a process that occurs at constant pressure. From Equation \(\PageIndex{10}\) we see that at constant pressure the change in enthalpy, ΔH of the system, defined as Hfinal − Hinitial, is equal to the heat gained or lost.
\[\Delta H = H_{final} -H_{initial} = q_{p} \]
Just as with ΔE, because enthalpy is a state function, the magnitude of ΔH depends on only the initial and final states of the system, not on the path taken. The enthalpy change is the same even if the process does not occur at constant pressure. Most importantly, the change in enthalpy for a reaction can be determined by measuring the flow of heat into or out of the system. As we will see below, there are also cases where we want to know the amount of heat generated by a reaction, as for example for combustion of fuel. In that case knowing the molar change in enthalpy provides the information needed.
Finally, looking at Equation 9.2.9 shows that for reactions where the volume does not change, or better put does not change much, ΔHrxn ~ΔErxn. As a practical matter, this includes all reactions where all the products and reactants are either in the solid, liquid or aqueous phases. This is not generally true when there are gases on either side of the equation, a question which we will discuss in the chapter on gases.
Note the Pattern
To find ΔH, measure qp.
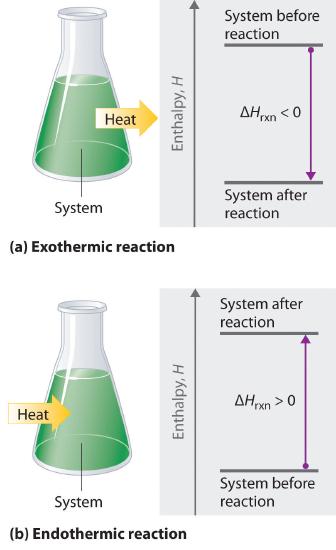
When we study energy changes in chemical reactions, the most important quantity is usually the enthalpy of reaction (ΔHrxn)The change in enthalpy that occurs during a chemical reaction., the change in enthalpy that occurs during a reaction (such as the dissolution of a piece of copper in nitric acid). If heat flows from a system to its surroundings, the enthalpy of the system decreases, so ΔHrxn is negative. Conversely, if heat flows from the surroundings to a system, the enthalpy of the system increases, so ΔHrxn is positive. Thus ΔHrxn < 0 for an exothermic reaction, and ΔHrxn > 0 for an endothermic reaction. In chemical reactions, bond breaking requires an input of energy and is therefore an endothermic process, whereas bond making releases energy, which is an exothermic process. The sign conventions for heat flow and enthalpy changes are summarized in the following table:
| Reaction Type | q | ΔHrxn |
|---|---|---|
| exothermic | < 0 | < 0 (heat flows from a system to its surroundings) |
| endothermic | > 0 | > 0 (heat flows from the surroundings to a system) |
If ΔHrxn is negative, then the enthalpy of the products is less than the enthalpy of the reactants; that is, an exothermic reaction is energetically downhill (part (a) in Figure \(\PageIndex{4}\) ). Conversely, if ΔHrxn is positive, then the enthalpy of the products is greater than the enthalpy of the reactants; thus, an endothermic reaction is energetically uphill (part (b) in Figure \(\PageIndex{4}\) ). Two important characteristics of enthalpy and changes in enthalpy are summarized in the following discussion.
Note the Pattern
Bond breaking requires an input of energy; bond making releases energy.
- Reversing a reaction or a process changes the sign of ΔH. Ice absorbs heat when it melts (electrostatic interactions are broken), so liquid water must release heat when it freezes (electrostatic interactions are formed):
\[ \begin{matrix}
heat+ H_{2}O(s) \rightarrow H_{2}O(l) & \Delta H > 0
\end{matrix} \]\[ \begin{matrix}
H_{2}O(l) \rightarrow H_{2}O(s) + heat & \Delta H < 0
\end{matrix} \]In both cases, the magnitude of the enthalpy change is the same; only the sign is different.
- Enthalpy is an extensive property (like mass). The magnitude of ΔH for a reaction is proportional to the amounts of the substances that react. For example, a large fire produces more heat than a single match, even though the chemical reaction—the combustion of wood—is the same in both cases. For this reason, the enthalpy change for a reaction is usually given in kilojoules per mole of a particular reactant or product. Consider Equation 9.2.12, which describes the reaction of aluminum with iron(III) oxide (Fe2O3) at constant pressure. According to the reaction stoichiometry, 2 mol of Fe, 1 mol of Al2O3, and 851.5 kJ of heat are produced for every 2 mol of Al and 1 mol of Fe2O3 consumed:
\[ 2Al\left (s \right )+Fe_{2}O_{3}\left (s \right ) \rightarrow 2Fe\left (s \right )+Al_{2}O_{3}\left (s \right )+ 815.5 \; kJ \]
Thus ΔH = −851.5 kJ/mol of Fe2O3. We can also describe ΔH for the reaction as −425.8 kJ/mol of Al: because 2 mol of Al are consumed in the balanced chemical equation, we divide −851.5 kJ by 2. When a value for ΔH, in kilojoules rather than kilojoules per mole, is written after the reaction, as in Equation 9.2.13, it is the value of ΔH corresponding to the reaction of the molar quantities of reactants as given in the balanced chemical equation:
\[ 2Al\left (s \right )+Fe_{2}O_{3}\left (s \right ) \rightarrow 2Fe\left (s \right )+Al_{2}O_{3}\left (s \right ) \;\;\;\; \Delta H_{rxn}= - 851.5 \; kJ \]
If 4 mol of Al and 2 mol of Fe2O3 react, the change in enthalpy is 2 × (−851.5 kJ) = −1703 kJ. We can summarize the relationship between the amount of each substance and the enthalpy change for this reaction as follows:
\[ - \dfrac{851.5 \; kJ}{2 \; mol \;Al} = - \dfrac{425.8 \; kJ}{1 \; mol \;Al} = - \dfrac{1703 \; kJ}{4 \; mol \; Al} \]
The relationship between the magnitude of the enthalpy change and the mass of reactants is illustrated in Example \(\PageIndex{1}\).
Certain parts of the world, such as southern California and Saudi Arabia, are short of freshwater for drinking. One possible solution to the problem is to tow icebergs from Antarctica and then melt them as needed. If ΔH is 6.01 kJ/mol for the reaction H2O(s) → H2O(l) at 0°C and constant pressure, how much energy would be required to melt a moderately large iceberg with a mass of 1.00 million metric tons (1.00 × 106 metric tons)? (A metric ton is 1000 kg.)
Given: energy per mole of ice and mass of iceberg
Asked for: energy required to melt iceberg
Strategy:
A Calculate the number of moles of ice contained in 1 million metric tons (1.00 × 106 metric tons) of ice.
B Calculate the energy needed to melt the ice by multiplying the number of moles of ice in the iceberg by the amount of energy required to melt 1 mol of ice.
Solution:
A Because enthalpy is an extensive property, the amount of energy required to melt ice depends on the amount of ice present. We are given ΔH for the process—that is, the amount of energy needed to melt 1 mol (or 18.015 g) of ice—so we need to calculate the number of moles of ice in the iceberg and multiply that number by ΔH (+6.01 kJ/mol):
\( \begin{matrix}
moles \; H_{2}O & = & 1.00\times 10^{6} \; metric \; tons H_{2}O \left ( \dfrac{1000 \; \cancel{kg}}{1 \; \cancel{metric \; ton}} \right ) \left ( \dfrac{1000 \; \cancel{g}}{1 \; \cancel{kg}} \right ) \left ( \dfrac{1 \; mol \; H_{2}O}{18.015 \; \cancel{g \; H_{2}O}} \right )\\
& = & 5.55\times 10^{10} \; mol H_{2}O
\end{matrix} \)
B The energy needed to melt the iceberg is thus
\( \left ( \dfrac{6.01 \; kJ}{\cancel{mol \; H_{2}O}} \right )\left ( 5.55 \times 10^{10} \; \cancel{mol \; H_{2}O} \right )= 3.34 \times 10^{11} \; kJ \)
Because so much energy is needed to melt the iceberg, this plan would require a relatively inexpensive source of energy to be practical. To give you some idea of the scale of such an operation, the amounts of different energy sources equivalent to the amount of energy needed to melt the iceberg are shown in the table below.
| Possible sources of the approximately 3.34 × 1011 kJ needed to melt a 1.00 × 106 metric ton iceberg |
|---|
| Combustion of 3.8 × 103 ft3 of natural gas |
| Combustion of 68,000 barrels of oil |
| Combustion of 15,000 tons of coal |
| 1.1 × 108 kilowatt-hours of electricity |
If 17.3 g of powdered aluminum are allowed to react with excess Fe2O3, how much heat is produced?
- Answer
-
273 kJ
Key Equations
definition of enthalpy
Equation \(\PageIndex{6}\) : H= E + PV
pressure-volume work
Equation \(\PageIndex{5}\) : w = −PΔV
enthalpy change at constant pressure
Equation \(\PageIndex{8}\) : ΔH = ΔE + PΔV
Equation \(\PageIndex{9}\) : ΔH = qp
Summary
In chemistry, the small part of the universe that we are studying is the system, and the rest of the universe is the surroundings. Open systems can exchange both matter and energy with their surroundings, closed systems can exchange energy but not matter with their surroundings, and isolated systems can exchange neither matter nor energy with their surroundings. A state function is a property of a system that depends on only its present state, not its history. A reaction or process in which heat is transferred from a system to its surroundings is exothermic. A reaction or process in which heat is transferred to a system from its surroundings is endothermic.
Enthalpy is a state function used to measure the heat transferred from a system to its surroundings or vice versa at constant pressure. Only the change in enthalpy (ΔH) can be measured. A negative ΔH means that heat flows from a system to its surroundings; a positive ΔH means that heat flows into a system from its surroundings. For a chemical reaction, the enthalpy of reaction (ΔHrxn) is the difference in enthalpy between products and reactants; the units of ΔHrxn are kilojoules per mole. Reversing a chemical reaction reverses the sign of ΔHrxn. The magnitude of ΔHrxn also depends on the physical state of the reactants and the products because processes such as melting solids or vaporizing liquids are also accompanied by enthalpy changes: the enthalpy of fusion (ΔHfus) and the enthalpy of vaporization (ΔHvap), respectively. The overall enthalpy change for a series of reactions is the sum of the enthalpy changes for the individual reactions, which is Hess’s law. The enthalpy of combustion (ΔHcomb) is the enthalpy change that occurs when a substance is burned in excess oxygen. The enthalpy of formation (ΔHf) is the enthalpy change that accompanies the formation of a compound from its elements. Standard enthalpies of formation (ΔHof) are determined under standard conditions: a pressure of 1 atm for gases and a concentration of 1 M for species in solution, with all pure substances present in their standard states (their most stable forms at 1 atm pressure and the temperature of the measurement). The standard heat of formation of any element in its most stable form is defined to be zero. The standard enthalpy of reaction (ΔHorxn) can be calculated from the sum of the standard enthalpies of formation of the products (each multiplied by its stoichiometric coefficient) minus the sum of the standard enthalpies of formation of the reactants (each multiplied by its stoichiometric coefficient)—the “products minus reactants” rule. The enthalpy of solution (ΔHsoln) is the heat released or absorbed when a specified amount of a solute dissolves in a certain quantity of solvent at constant pressure.
Key Takeaway
- Enthalpy is a state function whose change indicates the amount of heat transferred from a system to its surroundings or vice versa, at constant pressure.
Conceptual Problems
Please be sure you are familiar with the topics discussed in Essential Skills 4 (Section 9.9 ) before proceeding to the Conceptual Problems.
-
Heat implies the flow of energy from one object to another. Describe the energy flow in an
a. exothermic reaction.
b. endothermic reaction.
-
When a thermometer is suspended in an insulated thermos that contains a block of ice, the temperature recorded on the thermometer drops. Describe the direction of heat flow.
-
In each scenario, the system is defined as the mixture of chemical substances that undergoes a reaction. State whether each process is endothermic or exothermic.
- Water is added to sodium hydroxide pellets, and the flask becomes hot.
- The body metabolizes glucose, producing carbon dioxide and water.
- Ammonium nitrate crystals are dissolved in water, causing the solution to become cool.
-
In each scenario, the system is defined as the mixture of chemical substances that undergoes a reaction. Determine whether each process is endothermic or exothermic.
- Concentrated acid is added to water in a flask, and the flask becomes warm.
- Water evaporates from your skin, causing you to shiver.
- A container of ammonium nitrate detonates.
-
Is Earth’s environment an isolated system, an open system, or a closed system? Explain your answer.
-
Why is it impossible to measure the absolute magnitude of the enthalpy of an object or a compound?
-
Determine whether energy is consumed or released in each scenario. Explain your reasoning.
- A leaf falls from a tree.
- A motorboat maneuvers against a current.
- A child jumps rope.
- Dynamite detonates.
- A jogger sprints down a hill.
-
The chapter states that enthalpy is an extensive property. Why? Describe a situation that illustrates this fact.
-
The enthalpy of a system is affected by the physical states of the reactants and the products. Explain why.
-
Is the distance a person travels on a trip a state function? Why or why not?
-
Contributors
- Anonymous
Modified by Joshua Halpern


