4.9: Quantitative Analysis Using Titration
- Page ID
- 349390
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To use titration methods to analyze solutions quantitatively.
To determine the amounts or concentrations of substances present in a sample, chemists use a combination of chemical reactions and stoichiometric calculations in a methodology called quantitative analysisA methodology that combines chemical reactions and stoichiometric calculations to determine the amounts or concentrations of substances present in a sample.. Suppose, for example, we know the identity of a certain compound in a solution but not its concentration. If the compound reacts rapidly and completely with another reactant, we may be able to use the reaction to determine the concentration of the compound of interest. In a titrationAn experimental procedure in which a carefully measured volume of a solution of known concentration is added to a measured volume of a solution containing a compound whose concentration is to be determined., a carefully measured volume of a solution of known concentration, called the titrantThe solution of known concentration that is reacted with a compound in a solution of unknown concentration in a titration., is added to a measured volume of a solution containing a compound whose concentration is to be determined (the unknown). The reaction used in a titration can be an acid–base reaction, a precipitation reaction, or an oxidation–reduction reaction. In all cases, the reaction chosen for the analysis must be fast, complete, and specific; that is, only the compound of interest should react with the titrant. The equivalence pointThe point in a titration where a stoichiometric amount (i.e., the amount required to react completely with the unknown) of the titrant has been added. is reached when a stoichiometric amount of the titrant has been added—the amount required to react completely with the unknown.
Determining the Concentration of an Unknown Solution Using a Titration
The chemical nature of the species present in the unknown dictates which type of reaction is most appropriate and also how to determine the equivalence point. The volume of titrant added, its concentration, and the coefficients from the balanced chemical equation for the reaction allow us to calculate the total number of moles of the unknown in the original solution. Because we have measured the volume of the solution that contains the unknown, we can calculate the molarity of the unknown substance. This procedure is summarized graphically here:

The calcium salt of oxalic acid [Ca(O2CCO2)] is found in the sap and leaves of some vegetables, including spinach and rhubarb, and in many ornamental plants. Because oxalic acid and its salts are toxic, when a food such as rhubarb is processed commercially, the leaves must be removed, and the oxalate content carefully monitored.
The reaction of MnO4− with oxalic acid (HO2CCO2H) in acidic aqueous solution produces Mn2+ and CO2:
\( \begin{pmatrix}
MnO_{4}^{-}\left ( aq \right )+HO_{2}CCO_{2}H\left ( aq \right ) &\rightarrow Mn^{2+}\left ( aq \right )&+CO_{2}\left ( g \right )+H_{2}O\left ( l \right ) \\
purple & colorless &
\end{pmatrix} \notag \)
Because this reaction is rapid and goes to completion, potassium permanganate (KMnO4) is widely used as a reactant for determining the concentration of oxalic acid. The following video demonstrates the reaction
Figure \(\PageIndex{1}\) Redox reaction of potassium permanganate and oxalic acid
Suppose you stirred a 10.0 g sample of canned rhubarb with enough dilute H2SO4(aq) to obtain 127 mL of colorless solution. Because the added permanganate is rapidly consumed, adding small volumes of a 0.0247 M KMnO4 solution, which has a deep purple color, to the rhubarb extract does not initially change the color of the extract. When 15.4 mL of the permanganate solution have been added, however, the solution becomes a faint purple due to the presence of a slight excess of permanganate (Figure 8.9.1). If we assume that oxalic acid is the only species in solution that reacts with permanganate, what percentage of the mass of the original sample was calcium oxalate? The video below demonstrates the titration when small, measured amounts of a known permaganate solution are added. At the endpoint, the number of moles of permaganage added equals the number of moles of oxalate in the solution, thus determining how many moles of oxalate we started with
Figure 8.9.2 Titration of a permaganate solution with oxalic acid
As oxalic asci is added to the potassium permaginate solution the purple color a disappears as the permanganate is consumed. As more permanganate is added, eventually all the oxalate is oxidized, and a faint purple color from the presence of excess permanganate appears, marking the endpoint .
Given: equation, mass of sample, volume of solution, and molarity and volume of titrant
Asked for: mass percentage of unknown in sample
Strategy:
A Balance the chemical equation for the reaction using oxidation states.
B Calculate the number of moles of permanganate consumed by multiplying the volume of the titrant by its molarity. Then calculate the number of moles of oxalate in the solution by multiplying by the ratio of the coefficients in the balanced chemical equation. Because calcium oxalate contains a 1:1 ratio of Ca2+:−O2CCO2−, the number of moles of oxalate in the solution is the same as the number of moles of calcium oxalate in the original sample.
C Find the mass of calcium oxalate by multiplying the number of moles of calcium oxalate in the sample by its molar mass. Divide the mass of calcium oxalate by the mass of the sample and convert to a percentage to calculate the percentage by mass of calcium oxalate in the original sample.
Solution
A As in all other problems of this type, the first requirement is a balanced chemical equation for the reaction. Using oxidation states gives
\(2MnO_4^-(aq) + 5HO_2CCO_2H(aq) + 6H^+(aq) \rightarrow 2Mn^{2+}(aq) + 10CO_2(g) + 8H_2O(l) \notag \)
Thus each mole of MnO4− added consumes 2.5 mol of oxalic acid.
B Because we know the concentration of permanganate (0.0247 M) and the volume of permanganate solution that was needed to consume all the oxalic acid (15.4 mL), we can calculate the number of moles of MnO4− consumed. To do this we first convert the volume in mL to a volume in liters. Then simply multiplying the molarity of the solution by the volume in liters we find the number of moles of MnO4−
\( 15.4\; \cancel{mL}\left ( \frac{1 \: \cancel{L}}{1000\; \cancel{mL}} \right )\left ( \frac{0.0247\; mol\; MnO_{4}^{-}}{1\; \cancel{L}} \right )=3.80\times 10^{4\;} mol\; MnO_{4}^{-} \notag \)
The number of moles of oxalic acid, and thus oxalate, present can be calculated from the mole ratio of the reactants in the balanced chemical equation. We can abbreviate the table needed to calculate the number of moles of oxalic acid in the
\(\begin{align} moles\: HO_2 CCO_2 H & = 3 .80 \times 10^{-4}\: \cancel{mol\: MnO_4^-} \left( \dfrac{5\: mol\: HO_2 CCO_2 H} {2\:\cancel{mol\: MnO_4^-}} \right) \notag \\ &= 9 .50 \times 10^{-4}\: mol\: HO_2 CCO_2 H \notag \end{align} \)
C The problem asks for the percentage of calcium oxalate by mass in the original 10.0 g sample of rhubarb, so we need to know the mass of calcium oxalate that produced 9.50 × 10−4 mol of oxalic acid. Because calcium oxalate is Ca(O2CCO2), 1 mol of calcium oxalate gave 1 mol of oxalic acid in the initial acid extraction:
\(Ca(O_2CCO_2)(s) + 2H^+(aq) \rightarrow Ca^{2+}(aq) + HO_2CCO_2H(aq) \notag \)
The mass of calcium oxalate originally present was thus
\(\begin{align} mass\: of\: CaC_2 O_4 &= 9 .50 \times 10^{-4}\: \cancel{mol\: HO_2 CCO_2 H} \left( \dfrac{1\: \cancel{mol\: CaC_2 O_4}} {1\: \cancel{mol\: HO_2 CCO_2 H}} \right) \left( \dfrac{128 .10\: g\: CaC_2 O_4} {1\: \cancel{mol\: CaC_2 O_4}} \right) \notag \\ &= 0 .122\: g\: CaC_2 O_4 \notag \end{align}\)
The original sample contained 0.122 g of calcium oxalate per 10.0 g of rhubarb. The percentage of calcium oxalate by mass was thus
\( \% CaC_2 O_4 = \dfrac{0 .122\: g} {10 .0\: g} \times 100 = 1 .22\% \notag \)
Because the problem asked for the percentage by mass of calcium oxalate in the original sample rather than for the concentration of oxalic acid in the extract, we do not need to know the volume of the oxalic acid solution for this calculation.
Add text here.
Glutathione is a low-molecular-weight compound found in living cells that is produced naturally by the liver. Health-care providers give glutathione intravenously to prevent side effects of chemotherapy and to prevent kidney problems after heart bypass surgery. Its structure is as follows:
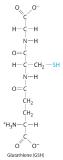
Glutathione is found in two forms: one abbreviated as GSH (indicating the presence of an –SH group) and the other as GSSG (the disulfide form, in which an S–S bond links two glutathione units). The GSH form is easily oxidized to GSSG by elemental iodine:
\(2GSH(aq) + I_2(aq) \rightarrow GSSG(aq) + 2HI(aq) \notag \)
A small amount of soluble starch is added as an indicator. Because starch reacts with excess I2 to give an intense blue color, the appearance of a blue color indicates that the equivalence point of the reaction has been reached.
Adding small volumes of a 0.0031 M aqueous solution of I2 to 194 mL of a solution that contains glutathione and a trace of soluble starch initially causes no change. After 16.3 mL of iodine solution have been added, however, a permanent pale blue color appears because of the formation of the starch-iodine complex. What is the concentration of glutathione in the original solution?
- Answer
-
5.2 × 10−4 M
Standard Solutions

The reaction of KHP with NaOH. As with all acid-base reactions, a salt is formed.
In Example \(\PageIndex{1}\), the concentration of the titrant was accurately known. The accuracy of any titration analysis depends on an accurate knowledge of the concentration of the titrant. Most titrants are first standardized; that is, their concentration is measured by titration with a standard solutionA solution whose concentration is precisely known., which is a solution whose concentration is known precisely. Only pure crystalline compounds that do not react with water or carbon dioxide are suitable for use in preparing a standard solution. One such compound is potassium hydrogen phthalate (KHP), a weak monoprotic acid suitable for standardizing solutions of bases such as sodium hydroxide. The reaction of KHP with NaOH is a simple acid–base reaction. If the concentration of the KHP solution is known accurately and the titration of a NaOH solution with the KHP solution is carried out carefully, then the concentration of the NaOH solution can be calculated precisely. The standardized NaOH solution can then be used to titrate a solution of an acid whose concentration is unknown.
Acid–Base Titrations
Because most common acids and bases are not intensely colored, a small amount of an acid–base indicator is usually added to detect the equivalence point in an acid–base titration. The point in the titration at which an indicator changes color is called the endpointThe point in a titration at which an indicator changes color.. The procedure is illustrated in Example 21.
The structure of vitamin C (ascorbic acid, a monoprotic acid) is as follows:
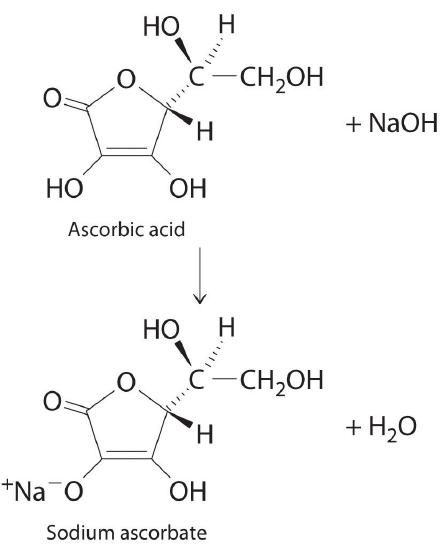
Ascorbic acid. The upper figure shows the three-dimensional representation of ascorbic acid. Hatched lines indicate bonds that are behind the plane of the paper, and wedged lines indicate bonds that are out of the plane of the paper.
An absence of vitamin C in the diet leads to the disease known as scurvy, a breakdown of connective tissue throughout the body and of dentin in the teeth. Because fresh fruits and vegetables rich in vitamin C are readily available in developed countries today, scurvy is not a major problem. In the days of slow voyages in wooden ships, however, scurvy was common. Ferdinand Magellan, the first person to sail around the world, lost more than 90% of his crew, many to scurvy. Although a diet rich in fruits and vegetables contains more than enough vitamin C to prevent scurvy, many people take supplemental doses of vitamin C, hoping that the extra amounts will help prevent colds and other illness.
Suppose a tablet advertised as containing 500 mg of vitamin C is dissolved in 100.0 mL of distilled water that contains a small amount of the acid–base indicator bromothymol blue, an indicator that is yellow in acid solution and blue in basic solution, to give a yellow solution. The addition of 53.5 mL of a 0.0520 M solution of NaOH results in a change to green at the endpoint, due to a mixture of the blue and yellow forms of the indicator What is the actual mass of vitamin C in the tablet? (The molar mass of ascorbic acid is 176.13 g/mol.)
The solution, containing bromothymol blue as an indicator, is initially yellow (a). The addition of a trace excess of NaOH causes the solution to turn green at the endpoint (b) and then blue.
Given: reactant, volume of sample solution, and volume and molarity of titrant
Asked for: mass of unknown
Strategy:
A Write the balanced chemical equation for the reaction and calculate the number of moles of base needed to neutralize the ascorbic acid.
B Using mole ratios, determine the amount of ascorbic acid consumed. Calculate the mass of vitamin C by multiplying the number of moles of ascorbic acid by its molar mass.
Solution
A Because ascorbic acid acts as a monoprotic acid, we can write the balanced chemical equation for the reaction as
\(HAsc(aq) + OH^-(aq) \rightarrow Asc^-(aq) + H_2O(l) \)
where HAsc is ascorbic acid and Asc− is ascorbate. The number of moles of OH− ions needed to neutralize the ascorbic acid is
\( moles\: OH^- = 53 .5\: \cancel{mL} \left( \dfrac{\cancel{1\: L}} {1000\: \cancel{mL}} \right) \left( \dfrac{0 .0520\: mol\: OH^-} {\cancel{1\: L}} \right) = 2 .78 \times 10^{-3}\: mol\: OH^- \)
B The mole ratio of the base added to the acid consumed is 1:1, so the number of moles of OH− added equals the number of moles of ascorbic acid present in the tablet:
\( mass\: ascorbic\: acid = 2 .78 \times 10^{-3}\: \cancel{mol\: HAsc} \left( \dfrac{176 .13\: g\: HAsc} {1 \: \cancel{mol\: HAsc}} \right) = 0 .490\: g\: HAsc \)
Because 0.490 g equals 490 mg, the tablet contains about 2% less vitamin C than advertised.
Vinegar is essentially a dilute solution of acetic acid in water. Vinegar is usually produced in a concentrated form and then diluted with water to give a final concentration of 4%–7% acetic acid; that is, a 4% m/v solution contains 4.00 g of acetic acid per 100 mL of solution. If a drop of bromothymol blue indicator is added to 50.0 mL of concentrated vinegar stock and 31.0 mL of 2.51 M NaOH are needed to turn the solution from yellow to green, what is the percentage of acetic acid in the vinegar stock? (Assume that the density of the vinegar solution is 1.00 g/mL.)
- Answer
-
9.35%
Summary
The concentration of a species in solution can be determined by quantitative analysis. One such method is a titration, in which a measured volume of a solution of one substance, the titrant, is added to a solution of another substance to determine its concentration. The equivalence point in a titration is the point at which exactly enough reactant has been added for the reaction to go to completion. A standard solution, a solution whose concentration is known precisely, is used to determine the concentration of the titrant. Many titrations, especially those that involve acid–base reactions, rely on an indicator. The point at which a color change is observed is the endpoint, which is close to the equivalence point if the indicator is chosen properly.
Key Takeaway
- Quantitative analysis of an unknown solution can be achieved using titration methods.
Conceptual Problems
-
The titration procedure is an application of the use of limiting reactants. Explain why this is so.
-
Explain how to determine the concentration of a substance using a titration.
-
Following are two graphs that illustrate how the pH of a solution varies during a titration. One graph corresponds to the titration of 100 mL 0.10 M acetic acid with 0.10 M NaOH, and the other corresponds to the titration of 100 mL 0.10 M NaOH with 0.10 M acetic acid. Which graph corresponds to which titration? Justify your answer.

-
Following are two graphs that illustrate how the pH of a solution varies during a titration. One graph corresponds to the titration of 100 mL 0.10 M ammonia with 0.10 M HCl, and the other corresponds to the titration of 100 mL 0.10 M NH4Cl with 0.10 M NaOH. Which graph corresponds to which titration? Justify your answer.

-
Following are two graphs that illustrate how the electrical conductivity of a solution varies during a titration. One graph corresponds to the titration of 100 mL 0.10 M Ba(OH)2 with 0.10 M H2SO4 , and the other corresponds to the titration of 100 mL of 0.10 M NaOH with 0.10 M H2SO4. Which graph corresponds to which titration? Justify your answer.

Answers
-
- titration of NaOH with acetic acid
- titration of acetic acid with NaOH
-
- titration of Ba(OH)2 with sulfuric acid
- titration of NaOH with sulfuric acid
Numerical Problems
-
A 10.00 mL sample of a 1.07 M solution of potassium hydrogen phthalate (KHP, formula mass = 204.22 g/mol) is diluted to 250.0 mL. What is the molarity of the final solution? How many grams of KHP are in the 10.00 mL sample?
-
What volume of a 0.978 M solution of NaOH must be added to 25.0 mL of 0.583 M HCl to completely neutralize the acid? How many moles of NaOH are needed for the neutralization?
-
A student was titrating 25.00 mL of a basic solution with an HCl solution that was 0.281 M. The student ran out of the HCl solution after having added 32.46 mL, so she borrowed an HCl solution that was labeled as 0.317 M. An additional 11.5 mL of the second solution was needed to complete the titration. What was the concentration of the basic solution?
Contributors
- Anonymous
Modified by Joshua Halpern (Howard University)


