4.5: Precipitation Reactions
- Page ID
- 349386
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To identify a precipitation reaction and predict solubilities
A precipitation reactionA subclass of an exchange reaction that yields an insoluble product (a precipitate) when two solutions are mixed. is a reaction that yields an insoluble product—a precipitateThe insoluble product that forms in a precipitation reaction.—when two solutions are mixed. In Section 3.4, we described a precipitation reaction in which a colorless solution of silver nitrate was mixed with a yellow-orange solution of potassium dichromate to give a reddish precipitate of silver dichromate:
\[ AgNO_3(aq) + K_2Cr_2O_7(aq) \rightarrow Ag_2Cr_2O_7(s) + KNO_3(aq) \]
This equation has the general form of an exchange reaction:
\[ AC + BD \rightarrow \underset{insoluble}{AD} + BC \]
Thus precipitation reactions are a subclass of exchange reactions that occur between ionic compounds when one of the products is insoluble. Because both components of each compound change partners, such reactions are sometimes called double-displacement reactions. Two important uses of precipitation reactions are to isolate metals that have been extracted from their ores and to recover precious metals for recycling.
Note the Pattern
Precipitation reactions are a subclass of exchange reactions.
Predicting Solubilities
Table \(\PageIndex{1}\) gives guidelines for predicting the solubility of a wide variety of ionic compounds. To determine whether a precipitation reaction will occur, we identify each species in the solution and then refer to Table \(\PageIndex{1}\) to see which, if any, combination(s) of cation and anion are likely to produce an insoluble salt. In doing so, it is important to recognize that soluble and insoluble are relative terms that span a wide range of actual solubilities. We will discuss solubilities in more detail in the second semester, where you will learn that very small amounts of the constituent ions remain in solution even after precipitation of an “insoluble” salt. For our purposes, however, we will assume that precipitation of an insoluble salt is complete.
Table \(\PageIndex{1}\) Guidelines for Predicting the Solubility of Ionic Compounds in Water
| Soluble | Exceptions | ||
| Rule 1 | most salts that contain an alkali metal (Li+, Na+, K+, Rb+, and Cs+) and ammonium (NH4+) | ||
| Rule 2 | most salts that contain the nitrate (NO3−) anion | ||
| Rule 3 | most salts of anions derived from monocarboxylic acids (e.g., CH3CO2−) | but not | silver acetate and salts of long-chain carboxylates |
| Rule 4 | most chloride, bromide, and iodide salts | but not | salts of metal ions located on the lower right side of the periodic table (e.g., Cu+, Ag+, Pb2+, and Hg22+). |
| Insoluble | Exceptions | ||
| Rule 5 | most salts that contain the hydroxide (OH−) and sulfide (S2−) anions | but not | salts of the alkali metals (group 1), the heavier alkaline earths (Ca2+, Sr2+, and Ba2+ in group 2), and the NH4+ ion. |
| Rule 6 | most carbonate (CO32−) and phosphate (PO43−) salts | but not | salts of the alkali metals or the NH4+ ion. |
| Rule 7 | most sulfate (SO42−) salts that contain main group cations with a charge ≥ +2 | but not | salts of +1 cations, Mg2+, and dipositive transition metal cations (e.g., Ni2+) |
Just as important as predicting the product of a reaction is knowing when a chemical reaction will not occur. Simply mixing solutions of two different chemical substances does not guarantee that a reaction will take place. For example, if 500 mL of a 1.0 M aqueous NaCl solution is mixed with 500 mL of a 1.0 M aqueous KBr solution, the final solution has a volume of 1.00 L and contains 0.50 M Na+(aq), 0.50 M Cl−(aq), 0.50 M K+(aq), and 0.50 M Br−(aq). As you will see in the following sections, none of these species reacts with any of the others. When these solutions are mixed, the only effect is to dilute each solution with the other (Figure \(\PageIndex{1}\) ).
Figure \(\PageIndex{1}\) The Effect of Mixing Aqueous KBr and NaCl Solutions
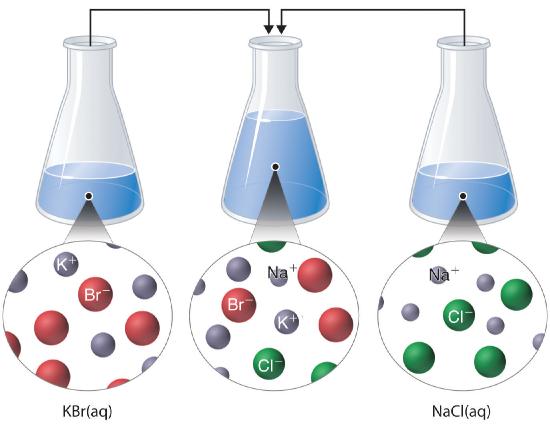
Because no net reaction occurs, the only effect is to dilute each solution with the other. (Water molecules are omitted from molecular views of the solutions for clarity.)
Using the information in Table \(\PageIndex{1}\), predict what will happen in each case involving strong electrolytes. Write the net ionic equation for any reaction that occurs.
- Aqueous solutions of barium chloride and lithium sulfate are mixed.
- Aqueous solutions of rubidium hydroxide and cobalt(II) chloride are mixed.
- Aqueous solutions of strontium bromide and aluminum nitrate are mixed.
- Solid lead(II) acetate is added to an aqueous solution of ammonium iodide.
Given: reactants
Asked for: reaction and net ionic equation
Strategy:
A Identify the ions present in solution and write the products of each possible exchange reaction.
B Refer to Table \(\PageIndex{1}\) to determine which, if any, of the products is insoluble and will therefore form a precipitate. If a precipitate forms, write the net ionic equation for the reaction.
Solution
- A Because barium chloride and lithium sulfate are strong electrolytes, each dissociates completely in water to give a solution that contains the constituent anions and cations. Mixing the two solutions initially gives an aqueous solution that contains Ba2+, Cl−, Li+, and SO42− ions. The only possible exchange reaction is to form LiCl and BaSO4:
B We now need to decide whether either of these products is insoluble. Table 8.2 shows that LiCl is soluble in water (rules 1 and 4), but BaSO4 is not soluble in water (rule 5). Thus BaSO4 will precipitate according to the net ionic equation
\(Ba^{2+}(aq) + SO_4^{2-}(aq) \rightarrow BaSO_4(s) \notag \)
Although soluble barium salts are toxic, BaSO4 is so insoluble that it can be used to diagnose stomach and intestinal problems without being absorbed into tissues. An outline of the digestive organs appears on x-rays of patients who have been given a “barium milkshake” or a “barium enema”—a suspension of very fine BaSO4 particles in water.
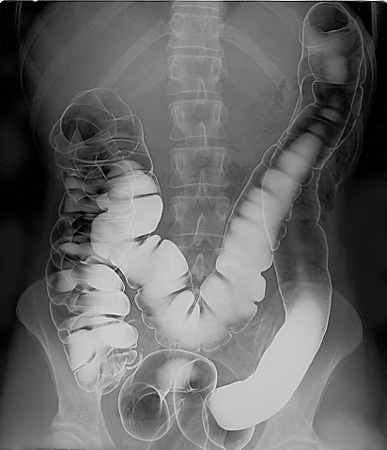
An x-ray of the digestive organs of a patient who has swallowed a “barium milkshake.” A barium milkshake is a suspension of very fine BaSO4 particles in water; the high atomic mass of barium makes it opaque to x-rays. From Wikipedia
- A Rubidium hydroxide and cobalt(II) chloride are strong electrolytes, so when aqueous solutions of these compounds are mixed, the resulting solution initially contains Rb+, OH−, Co2+, and Cl− ions. The possible products of an exchange reaction are rubidium chloride and cobalt(II) hydroxide):
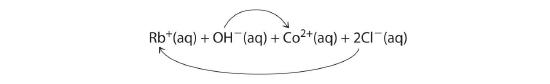
B According to Table \(\PageIndex{1}\), RbCl is soluble (rules 1 and 4), but Co(OH)2 is not soluble (rule 5). Hence Co(OH)2 will precipitate according to the following net ionic equation:
\(Co^{2+}(aq) + 2OH^-(aq) \rightarrow Co(OH)_2(s) \notag \)
- A When aqueous solutions of strontium bromide and aluminum nitrate are mixed, we initially obtain a solution that contains Sr2+, Br−, Al3+, and NO3− ions. The two possible products from an exchange reaction are aluminum bromide and strontium nitrate:

B According to Table \(\PageIndex{1}\) both AlBr3 (rule 4) and Sr(NO3)2 (rule 2) are soluble. Thus no net reaction will occur.
- A According to Table \(\PageIndex{1}\), lead acetate is soluble (rule 3). Thus solid lead acetate dissolves in water to give Pb2+ and CH3CO2− ions. Because the solution also contains NH4+ and I− ions, the possible products of an exchange reaction are ammonium acetate and lead(II) iodide:
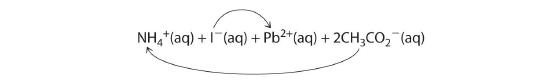
B According to Table 8.2, ammonium acetate is soluble (rules 1 and 3), but PbI2 is insoluble (rule 4). Thus Pb(C2H3O2)2 will dissolve, and PbI2 will precipitate. The net ionic equation is as follows:
\(Pb^{2+} (aq) + 2I^-(aq) \rightarrow PbI_2(s) \notag \)
Using the information in Table \(\PageIndex{1}\), predict what will happen in each case involving strong electrolytes. Write the net ionic equation for any reaction that occurs.
- An aqueous solution of strontium hydroxide is added to an aqueous solution of iron(II) chloride.
- Solid potassium phosphate is added to an aqueous solution of mercury(II) perchlorate.
- Solid sodium fluoride is added to an aqueous solution of ammonium formate.
- Aqueous solutions of calcium bromide and cesium carbonate are mixed.
- Answer
-
- \(Fe^{2+}(aq) + 2OH^-(aq) \rightarrow Fe(OH)_2(s)\)
- \(2PO_4^{3-}(aq) + 3Hg^{2+}(aq) \rightarrow Hg_3(PO_4)_2(s)\)
- \(NaF(s)\) dissolves; no net reaction
- \(Ca^{2+}(aq) + CO_3^{2-}(aq) \rightarrow CaCO_3(s)\)
Precipitation Reactions in Photography
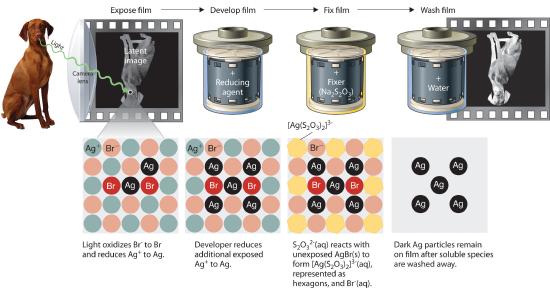
Precipitation reactions can be used to recover silver from solutions used to develop conventional photographic film. Although largely supplanted by digital photography, conventional methods are often used for artistic purposes. Silver bromide is an off-white solid that turns black when exposed to light, which is due to the formation of small particles of silver metal. Black-and-white photography uses this reaction to capture images in shades of gray, with the darkest areas of the film corresponding to the areas that received the most light. The first step in film processing is to enhance the black/white contrast by using a developer to increase the amount of black. The developer is a reductant: because silver atoms catalyze the reduction reaction, grains of silver bromide that have already been partially reduced by exposure to light react with the reductant much more rapidly than unexposed grains.
After the film is developed, any unexposed silver bromide must be removed by a process called “fixing”; otherwise, the entire film would turn black with additional exposure to light. Although silver bromide is insoluble in water, it is soluble in a dilute solution of sodium thiosulfate (Na2S2O3; photographer’s hypo) because of the formation of [Ag(S2O3)2]3− ions. Thus washing the film with thiosulfate solution dissolves unexposed silver bromide and leaves a pattern of metallic silver granules that constitutes the negative. This procedure is summarized in Figure \(\PageIndex{2}\). The negative image is then projected onto paper coated with silver halides, and the developing and fixing processes are repeated to give a positive image. (Color photography works in much the same way, with a combination of silver halides and organic dyes superimposed in layers.) “Instant photo” operations can generate more than a hundred gallons of dilute silver waste solution per day. Recovery of silver from thiosulfate fixing solutions involves first removing the thiosulfate by oxidation and then precipitating Ag+ ions with excess chloride ions.
Figure \(\PageIndex{2}\) Outline of the Steps Involved in Producing a Black-and-White Photograph
A silver recovery unit can process 1500 L of photographic silver waste solution per day. Adding excess solid sodium chloride to a 500 mL sample of the waste (after removing the thiosulfate as described previously) gives a white precipitate that, after filtration and drying, consists of 3.73 g of AgCl. What mass of NaCl must be added to the 1500 L of silver waste to ensure that all the Ag+ ions precipitate?
Given: volume of solution of one reactant and mass of product from a sample of reactant solution
Asked for: mass of second reactant needed for complete reaction
Strategy:
A Write the net ionic equation for the reaction. Calculate the number of moles of AgCl obtained from the 500 mL sample and then determine the concentration of Ag+ in the sample by dividing the number of moles of AgCl formed by the volume of solution.
B Determine the total number of moles of Ag+ in the 1500 L solution by multiplying the Ag+ concentration by the total volume.
C Use mole ratios to calculate the number of moles of chloride needed to react with Ag+. Obtain the mass of NaCl by multiplying the number of moles of NaCl needed by its molar mass.
Solution
We can use the data provided to determine the concentration of Ag+ ions in the waste, from which the number of moles of Ag+ in the entire waste solution can be calculated. From the net ionic equation, we can determine how many moles of Cl− are needed, which in turn will give us the mass of NaCl necessary.
A The first step is to write the net ionic equation for the reaction:
\(Cl^-(aq) + Ag^+(aq) \rightarrow AgCl(s) \notag \)
We know that 500 mL of solution produced 3.73 g of AgCl. We can convert this value to the number of moles of AgCl as follows:
\( moles\: AgCl = \dfrac{grams\: AgCl} {molar\: mass\: AgCl} = 3 .73\: \cancel{g\: AgCl} \left( \dfrac{1\: mol\: AgCl} {143 .32\: \cancel{g\: AgCl}} \right) = 0 .0260\: mol\: AgCl \)
Therefore, the 500 mL sample of the solution contained 0.0260 mol of Ag+. The Ag+ concentration is determined as follows:
\( [Ag^+ ] = \dfrac{moles\: Ag^+} {liters\: soln} = \dfrac{0 .0260\: mol\: AgCl} {0 .500\: L} = 0 .0520\: M \)
B The total number of moles of Ag+ present in 1500 L of solution is as follows:
\( moles\: Ag^+ = 1500\: \cancel{L} \left( \dfrac{0 .520\: mol} {1\: \cancel{L}} \right) = 78 .1\: mol\: Ag^+ \)
C According to the net ionic equation, one Cl− ion is required for each Ag+ ion. Thus 78.1 mol of NaCl are needed to precipitate the silver. The corresponding mass of NaCl is
\( mass\: NaCl = 78 .1 \: \cancel{mol\: NaCl} \left( \dfrac{58 .44\: g\: NaCl} {1\: \cancel{mol\: NaCl}} \right) = 4560\: g\: NaCl = 4 .56\: kg\: NaCl \)
Note that 78.1 mol of AgCl correspond to 8.43 kg of metallic silver, which is worth about $7983 at 2011 prices ($32.84 per troy ounce). Silver recovery may be economically attractive as well as ecologically sound, although the procedure outlined is becoming nearly obsolete for all but artistic purposes with the growth of digital photography.
Because of its toxicity, arsenic is the active ingredient in many pesticides. The arsenic content of a pesticide can be measured by oxidizing arsenic compounds to the arsenate ion (AsO43−), which forms an insoluble silver salt (Ag3AsO4). Suppose you are asked to assess the purity of technical grade sodium arsenite (NaAsO2), the active ingredient in a pesticide used against termites. You dissolve a 10.00 g sample in water, oxidize it to arsenate, and dilute it with water to a final volume of 500 mL. You then add excess AgNO3 solution to a 50.0 mL sample of the arsenate solution. The resulting precipitate of Ag3AsO4 has a mass of 3.24 g after drying. What is the percentage by mass of NaAsO2 in the original sample?
- Answer
-
91.0%
Summary
In a precipitation reaction, a subclass of exchange reactions, an insoluble material (a precipitate) forms when solutions of two substances are mixed. To predict the product of a precipitation reaction, all species initially present in the solutions are identified, as are any combinations likely to produce an insoluble salt.
Key Takeaway
- Predicting the solubility of ionic compounds in water can give insight into whether or not a reaction will occur.
Conceptual Problems
-
Predict whether mixing each pair of solutions will result in the formation of a precipitate. If so, identify the precipitate.
- FeCl2(aq) + Na2S(aq)
- NaOH(aq) + H3PO4(aq)
- ZnCl2(aq) + (NH4)2S(aq)
-
Predict whether mixing each pair of solutions will result in the formation of a precipitate. If so, identify the precipitate.
- KOH(aq) + H3PO4(aq)
- K2CO3(aq) + BaCl2(aq)
- Ba(NO3)2(aq) + Na2SO4(aq)
-
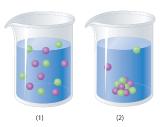
Which representation best corresponds to an aqueous solution originally containing each of the following?
- 1 M NH4Cl
- 1 M NaO2CCH3
- 1 M NaOH + 1 M HCl
- 1 M Ba(OH)2 + 1 M H2SO4
-
Which representation in Problem 3 best corresponds to an aqueous solution originally containing each of the following?
- 1 M CH3CO2H + 1 M NaOH
- 1 M NH3 + 1 M HCl
- 1 M Na2CO3 + 1 M H2SO4
- 1 M CaCl2 + 1 M H3PO4
Answer
-
- 1
- 1
- 1
- 2
Numerical Problems
-
What mass of precipitate would you expect to obtain by mixing 250 mL of a solution containing 4.88 g of Na2CrO4 with 200 mL of a solution containing 3.84 g of AgNO3? What is the final nitrate ion concentration?
-
Adding 10.0 mL of a dilute solution of zinc nitrate to 246 mL of 2.00 M sodium sulfide produced 0.279 g of a precipitate. How many grams of zinc(II) nitrate and sodium sulfide were consumed to produce this quantity of product? What was the concentration of each ion in the original solutions? What is the concentration of the sulfide ion in solution after the precipitation reaction, assuming no further reaction?
Answer
-
3.75 g Ag2CrO4; 5.02 × 10−2 M nitrate



