17.6: Reaction Mechanisms
- Page ID
- 78611
↵
- Distinguish net reactions from elementary reactions (steps)
- Identify the molecularity of elementary reactions
- Write a balanced chemical equation for a process given its reaction mechanism
- Derive the rate law consistent with a given reaction mechanism
A balanced equation for a chemical reaction indicates what is reacting and what is produced, but it reveals nothing about how the reaction actually takes place. The reaction mechanism (or reaction path) is the process, or pathway, by which a reaction occurs. A chemical reaction often occurs in steps, although it may not always be obvious to an observer. The decomposition of ozone, for example, appears to follow a mechanism with two steps:
\[\ce{O3}(g)⟶\ce{O2}(g)+\ce{O}\\
\ce{O}+\ce{O3}(g)⟶\ce{2O2}(g) \label{12.7.1} \]
We call each step in a reaction mechanism an elementary reaction. Elementary reactions occur exactly as they are written and cannot be broken down into simpler steps. Elementary reactions add up to the overall reaction, which, for the decomposition, is:
\[\ce{2O3}(g)⟶\ce{3O2}(g) \label{12.7.2} \]
Notice that the oxygen atom produced in the first step of this mechanism is consumed in the second step and therefore does not appear as a product in the overall reaction. Species that are produced in one step and consumed in a subsequent step are called intermediates.
While the overall reaction equation for the decomposition of ozone indicates that two molecules of ozone react to give three molecules of oxygen, the mechanism of the reaction does not involve the collision and reaction of two ozone molecules. Rather, it involves a molecule of ozone decomposing to an oxygen molecule and an intermediate oxygen atom; the oxygen atom then reacts with a second ozone molecule to give two oxygen molecules. These two elementary reactions occur exactly as they are shown in the reaction mechanism.
Unimolecular Elementary Reactions
The molecularity of an elementary reaction is the number of reactant species (atoms, molecules, or ions). For example, a unimolecular reaction involves the rearrangement of a single reactant species to produce one or more molecules of product:
\[A⟶\ce{products} \label{12.7.2b} \]
The rate equation for a unimolecular reaction is:
\[\ce{rate}=k[A] \label{12.7.3} \]
A unimolecular reaction may be one of several elementary reactions in a complex mechanism. For example, the reaction:
\[\ce{O3 ⟶ O2 + O} \label{12.7.4} \]
illustrates a unimolecular elementary reaction that occurs as one part of a two-step reaction mechanism. However, some unimolecular reactions may have only a single reaction in the reaction mechanism. (In other words, an elementary reaction can also be an overall reaction in some cases.) For example, the gas-phase decomposition of cyclobutane, C4H8, to ethylene, C2H4, occurs via a unimolecular, single-step mechanism:
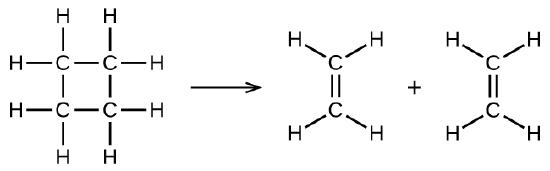
For these unimolecular reactions to occur, all that is required is the separation of parts of single reactant molecules into products.
Chemical bonds do not simply fall apart during chemical reactions. Energy is required to break chemical bonds. The activation energy for the decomposition of C4H8, for example, is 261 kJ per mole. This means that it requires 261 kilojoules to distort one mole of these molecules into activated complexes that decompose into products:

In a sample of C4H8, a few of the rapidly moving C4H8 molecules collide with other rapidly moving molecules and pick up additional energy. When the C4H8 molecules gain enough energy, they can transform into an activated complex, and the formation of ethylene molecules can occur. In effect, a particularly energetic collision knocks a C4H8 molecule into the geometry of the activated complex. However, only a small fraction of gas molecules travel at sufficiently high speeds with large enough kinetic energies to accomplish this. Hence, at any given moment, only a few molecules pick up enough energy from collisions to react.
The rate of decomposition of C4H8 is directly proportional to its concentration. Doubling the concentration of C4H8 in a sample gives twice as many molecules per liter. Although the fraction of molecules with enough energy to react remains the same, the total number of such molecules is twice as great. Consequently, there is twice as much C4H8 per liter, and the reaction rate is twice as fast:
\[\ce{rate}=−\dfrac{Δ[\ce{C4H8}]}{Δt}=k[\ce{C4H8}] \label{12.7.5} \]
A similar relationship applies to any unimolecular elementary reaction; the reaction rate is directly proportional to the concentration of the reactant, and the reaction exhibits first-order behavior. The proportionality constant is the rate constant for the particular unimolecular reaction.
Bimolecular Elementary Reactions
The collision and combination of two molecules or atoms to form an activated complex in an elementary reaction is called a bimolecular reaction. There are two types of bimolecular elementary reactions:
\[A+B⟶\ce{products} \label{12.7.6} \]
and
\[2A⟶\ce{products} \label{12.7.7} \]
For the first type, in which the two reactant molecules are different, the rate law is first-order in A and first order in B:
\[\ce{rate}=k[A][B] \label{12.7.8} \]
For the second type, in which two identical molecules collide and react, the rate law is second order in A:
\[\ce{rate}=k[A][A]=k[A]^2 \label{12.7.9} \]
Some chemical reactions have mechanisms that consist of a single bimolecular elementary reaction. One example is the reaction of nitrogen dioxide with carbon monoxide:
\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{NO}(g)+\ce{CO2}(g) \label{12.7.10} \]
(see Figure \(\PageIndex{1}\))

Bimolecular elementary reactions may also be involved as steps in a multistep reaction mechanism. The reaction of atomic oxygen with ozone is one example:
\[\ce{O}(g)+\ce{O3}(g)⟶\ce{2O2}(g) \label{12.7.12} \]
Termolecular Elementary Reactions
An elementary termolecular reaction involves the simultaneous collision of three atoms, molecules, or ions. Termolecular elementary reactions are uncommon because the probability of three particles colliding simultaneously is less than one one-thousandth of the probability of two particles colliding. There are, however, a few established termolecular elementary reactions. The reaction of nitric oxide with oxygen appears to involve termolecular steps:
\[\ce{2NO + O2 ⟶ 2NO2}\\
\ce{rate}=k[\ce{NO}]^2[\ce{O2}] \label{12.7.13} \]
Likewise, the reaction of nitric oxide with chlorine appears to involve termolecular steps:
\[\ce{2NO + Cl2 ⟶ 2NOCl}\\
\ce{rate}=k[\ce{NO}]^2[\ce{Cl2}] \label{12.7.14} \]
Relating Reaction Mechanisms to Rate Laws
It's often the case that one step in a multistep reaction mechanism is significantly slower than the others. Because a reaction cannot proceed faster than its slowest step, this step will limit the rate at which the overall reaction occurs. The slowest step is therefore called the rate-limiting step (or rate-determining step) of the reaction Figure \(\PageIndex{2}\).

As described earlier, rate laws may be derived directly from the chemical equations for elementary reactions. This is not the case, however, for ordinary chemical reactions. The balanced equations most often encountered represent the overall change for some chemical system, and very often this is the result of some multistep reaction mechanisms. In every case, we must determine the overall rate law from experimental data and deduce the mechanism from the rate law (and sometimes from other data). The reaction of NO2 and CO provides an illustrative example:
\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{CO2}(g)+\ce{NO}(g) \nonumber \]
For temperatures above 225 °C, the rate law has been found to be:
\[\ce{rate}=k[\ce{NO2}][\ce{CO}] \nonumber \]
The reaction is first order with respect to NO2 and first-order with respect to CO. This is consistent with a single-step bimolecular mechanism and it is possible that this is the mechanism for this reaction at high temperatures.
At temperatures below 225 °C, the reaction is described by a rate law that is second order with respect to NO2:
\[\ce{rate}=k[\ce{NO2}]^2 \nonumber \]
This is consistent with a mechanism that involves the following two elementary reactions, the first of which is slower and is therefore the rate-determining step:
\[\ce{NO2}(g)+\ce{NO2}(g)⟶\ce{NO3}(g)+\ce{NO}(g)\:\ce{(slow)}\\
\ce{NO3}(g)+\ce{CO}(g)⟶\ce{NO2}(g)+\ce{CO2}(g)\:\ce{(fast)} \nonumber \]
The rate-determining step gives a rate law showing second-order dependence on the NO2 concentration, and the sum of the two equations gives the net overall reaction.
In general, when the rate-determining (slower) step is the first step in a mechanism, the rate law for the overall reaction is the same as the rate law for this step. However, when the rate-determining step is preceded by a step involving an equilibrium reaction, the rate law for the overall reaction may be more difficult to derive.
An elementary reaction is at equilibrium when it proceeds in both the forward and reverse directions at equal rates. Consider the dimerization of NO to N2O2, with k1 used to represent the rate constant of the forward reaction and k-1 used to represent the rate constant of the reverse reaction:
\[\ce{NO + NO ⇌ N2O2} \nonumber \]
\[\ce{rate_{forward}=rate_{reverse}} \nonumber \]
\[k_1[\ce{NO}]^2=k_{−1}[\ce{N2O2}] \nonumber \]
If N2O2 was an intermediate in a mechanism, this expression could be rearranged to represent the concentration of N2O2 in the overall rate law expression using algebraic manipulation:
\[\mathrm{\left(\dfrac{k_1[NO]^2}{k_{−1}}\right)=[N_2O_2]} \nonumber \]
However, once again, intermediates cannot be listed as part of the overall rate law expression, though they can be included in an individual elementary reaction of a mechanism. Example \(\PageIndex{1}\) will illustrate how to derive overall rate laws from mechanisms involving equilibrium steps preceding the rate-determining step.
Mechanism Nitryl chloride (NO2Cl) decomposes to nitrogen dioxide (NO2) and chlorine gas (Cl2) according to the following mechanism:
- \(\ce{2NO2Cl}(g)⇌\ce{ClO2}(g)+\ce{N2O}(g)+\ce{ClO}(g)\) (fast, k1 represents the rate constant for the forward reaction and k−1 the rate constant for the reverse reaction)
- \(\ce{N2O}(g)+\ce{ClO2}(g)⇌\ce{NO2}(g)+\ce{NOCl}(g)\) (fast, k2 for the forward reaction, k−2 for the reverse reaction)
- \(\ce{NOCl + ClO ⟶ NO2 + Cl2}\) (slow, k3 the rate constant for the forward reaction)
Determine the overall reaction, write the rate law expression for each elementary reaction, identify any intermediates, and determine the overall rate law expression.
Solution
For the overall reaction, simply sum the three steps, cancel intermediates, and combine like formulas:
\[\ce{2NO2Cl}(g)⟶\ce{2NO2}(g)+\ce{Cl2}(g) \nonumber \]
Next, write the rate law expression for each elementary reaction. Remember that for elementary reactions that are part of a mechanism, the rate law expression can be derived directly from the stoichiometry:
\[\begin{align*}
k_1\ce{[NO2Cl]2}&=k_{−1}\ce{[ClO2][N2O][ClO]}\\
k_2\ce{[N2O][ClO2]}&=k_{−2}\ce{[NO2][NOCl]}\\
\ce{Rate}&=k_3\ce{[NOCl][ClO]}
\end{align*} \nonumber \]
The third step, which is the slow step, is the rate-determining step. Therefore, the overall rate law expression could be written as Rate = k3 [NOCl][ClO]. However, both NOCl and ClO are intermediates. Algebraic expressions must be used to represent [NOCl] and [ClO] such that no intermediates remain in the overall rate law expression.
- Using elementary reaction 1, \(\ce{[ClO]}=\dfrac{k_1\ce{[NO2Cl]^2}}{k_{−1}\ce{[ClO2][N2O]}}\).
- Using elementary reaction 2, \(\ce{[NOCl]}=\dfrac{k_2\ce{[N2O][ClO2]}}{k_{−2}\ce{[NO2]}}\).
Now substitute these algebraic expressions into the overall rate law expression and simplify:
\[\begin{align*}
\ce{rate}&=k_3\left(\dfrac{k_2\ce{[N2O][ClO2]}}{k_{−2}\ce{[NO2]}}\right)\left(\dfrac{k_1\ce{[NO2Cl]^2}}{k_{−1}\ce{[ClO2][N2O]}}\right)\\
\ce{rate}&=\dfrac{k_3k_2k_1\ce{[NO2Cl]^2}}{k_{−2}k_{−1}\ce{[NO2]}}
\end{align*} \nonumber \]
Notice that this rate law shows an inverse dependence on the concentration of one of the product species, consistent with the presence of an equilibrium step in the reaction mechanism.
Atomic chlorine in the atmosphere reacts with ozone in the following pair of elementary reactions:
\(\ce{Cl}+\ce{O3}(g)⟶\ce{ClO}(g)+\ce{O2}(g)\hspace{20px}(\textrm{rate constant }k_1)\)
Determine the overall reaction, write the rate law expression for each elementary reaction, identify any intermediates, and determine the overall rate law expression.
- Answer
-
- overall reaction: \(\ce{O3}(g)+\ce{O}⟶\ce{2O2}(g)\)
- rate1 = k1[O3][Cl]; rate2 = k2[ClO][O]
- intermediate: ClO(g)
- overall rate = k2k1[O3][Cl][O]
Summary
The sequence of individual steps, or elementary reactions, by which reactants are converted into products during the course of a reaction is called the reaction mechanism. The overall rate of a reaction is determined by the rate of the slowest step, called the rate-determining step. Unimolecular elementary reactions have first-order rate laws, while bimolecular elementary reactions have second-order rate laws. By comparing the rate laws derived from a reaction mechanism to that determined experimentally, the mechanism may be deemed either incorrect or plausible.
Footnotes
- This question is taken from the Chemistry Advanced Placement Examination and is used with the permission of the Educational Testing Service.
Glossary
- bimolecular reaction
- elementary reaction involving the collision and combination of two reactant species
- elementary reaction
- reaction that takes place precisely as depicted in its chemical equation
- intermediate
- molecule or ion produced in one step of a reaction mechanism and consumed in another
- molecularity
- number of reactant species (atoms, molecules or ions) involved in an elementary reaction
- rate-determining step
- (also, rate-limiting step) slowest elementary reaction in a reaction mechanism; determines the rate of the overall reaction
- reaction mechanism
- stepwise sequence of elementary reactions by which a chemical change takes place
- termolecular reaction
- elementary reaction involving the simultaneous collision and combination of three reactant species
- unimolecular reaction
- elementary reaction involving the rearrangement of a single reactant species to produce one or more molecules of product


