14.1: Brønsted-Lowry Acids and Bases
- Page ID
- 78622
- Identify acids, bases, and conjugate acid-base pairs according to the Brønsted-Lowry definition
- Write equations for acid and base ionization reactions
- Use the ion-product constant for water to calculate hydronium and hydroxide ion concentrations
- Describe the acid-base behavior of amphiprotic substances
Acids and bases have been known for a long time. When Robert Boyle characterized them in 1680, he noted that acids dissolve many substances, change the color of certain natural dyes (for example, they change litmus from blue to red), and lose these characteristic properties after coming into contact with alkalis (bases). In the eighteenth century, it was recognized that acids have a sour taste, react with limestone to liberate a gaseous substance (now known to be CO2), and interact with alkalis to form neutral substances. In 1815, Humphry Davy contributed greatly to the development of the modern acid-base concept by demonstrating that hydrogen is the essential constituent of acids. Around that same time, Joseph Louis Gay-Lussac concluded that acids are substances that can neutralize bases and that these two classes of substances can be defined only in terms of each other. The significance of hydrogen was reemphasized in 1884 when Svante Arrhenius defined an acid as a compound that dissolves in water to yield hydrogen cations (now recognized to be hydronium ions) and a base as a compound that dissolves in water to yield hydroxide anions.
In an earlier chapter on chemical reactions, we defined acids and bases as Arrhenius did: We identified an acid as a compound that dissolves in water to yield hydronium ions (H3O+) and a base as a compound that dissolves in water to yield hydroxide ions (\(\ce{OH-}\)). This definition is not wrong; it is simply limited.
Later, we extended the definition of an acid or a base using the more general definition proposed in 1923 by the Danish chemist Johannes Brønsted and the English chemist Thomas Lowry. Their definition centers on the proton, \(\ce{H^+}\). A proton is what remains when a normal hydrogen atom, \(\ce{^1_1H}\), loses an electron. A compound that donates a proton to another compound is called a Brønsted-Lowry acid, and a compound that accepts a proton is called a Brønsted-Lowry base. An acid-base reaction is the transfer of a proton from a proton donor (acid) to a proton acceptor (base). In a subsequent chapter of this text we will introduce the most general model of acid-base behavior introduced by the American chemist G. N. Lewis.
Acids may be compounds such as HCl or H2SO4, organic acids like acetic acid (\(\ce{CH_3COOH}\)) or ascorbic acid (vitamin C), or H2O. Anions (such as \(\ce{HSO_4^-}\), \(\ce{H_2PO_4^-}\), \(\ce{HS^-}\), and \(\ce{HCO_3^-}\)) and cations (such as \(\ce{H_3O^+}\), \(\ce{NH_4^+}\), and \(\ce{[Al(H_2O)_6]^{3+}}\)) may also act as acids. Bases fall into the same three categories. Bases may be neutral molecules (such as \(\ce{H_2O}\), \(\ce{NH_3}\), and \(\ce{CH_3NH_2}\)), anions (such as \(\ce{OH^-}\), \(\ce{HS^-}\), \(\ce{HCO_3^-}\), \(\ce{CO_3^{2−}}\), \(\ce{F^-}\), and \(\ce{PO_4^{3−}}\)), or cations (such as \(\ce{[Al(H_2O)_5OH]^{2+}}\)). The most familiar bases are ionic compounds such as \(\ce{NaOH}\) and \(\ce{Ca(OH)_2}\), which contain the hydroxide ion, \(\ce{OH^-}\). The hydroxide ion in these compounds accepts a proton from acids to form water:
\[\ce{H^+ + OH^- \rightarrow H_2O} \label{14.11} \]
We call the product that remains after an acid donates a proton the conjugate base of the acid. This species is a base because it can accept a proton (to re-form the acid):
\[\text{acid} \rightleftharpoons \text{proton} + \text{conjugate base}\label{14.12a} \]
\[\ce{HF \rightleftharpoons H^+ + F^-} \label{14.12b} \]
\[\ce{H_2SO_4 \rightleftharpoons H^+ + HSO_4^{−}}\label{14.12c} \]
\[\ce{H_2O \rightleftharpoons H^+ + OH^-}\label{14.12d} \]
\[\ce{HSO_4^- \rightleftharpoons H^+ + SO_4^{2−}}\label{14.12e} \]
\[\ce{NH_4^+ \rightleftharpoons H^+ + NH_3} \label{14.12f} \]
We call the product that results when a base accepts a proton the base’s conjugate acid. This species is an acid because it can give up a proton (and thus re-form the base):
\[\text{base} + \text{proton} \rightleftharpoons \text{conjugate acid} \label{14.13a} \]
\[\ce{OH^- +H^+ \rightleftharpoons H2O}\label{14.13b} \]
\[\ce{H_2O + H^+ \rightleftharpoons H3O+}\label{14.13c} \]
\[\ce{NH_3 +H^+ \rightleftharpoons NH4+}\label{14.13d} \]
\[\ce{S^{2-} +H^+ \rightleftharpoons HS-}\label{14.13e} \]
\[\ce{CO_3^{2-} +H^+ \rightleftharpoons HCO3-}\label{14.13f} \]
\[\ce{F^- +H^+ \rightleftharpoons HF} \label{14.13g} \]
In these two sets of equations, the behaviors of acids as proton donors and bases as proton acceptors are represented in isolation. In reality, all acid-base reactions involve the transfer of protons between acids and bases. For example, consider the acid-base reaction that takes place when ammonia is dissolved in water. A water molecule (functioning as an acid) transfers a proton to an ammonia molecule (functioning as a base), yielding the conjugate base of water, \(\ce{OH^-}\), and the conjugate acid of ammonia, \(\ce{NH4+}\):
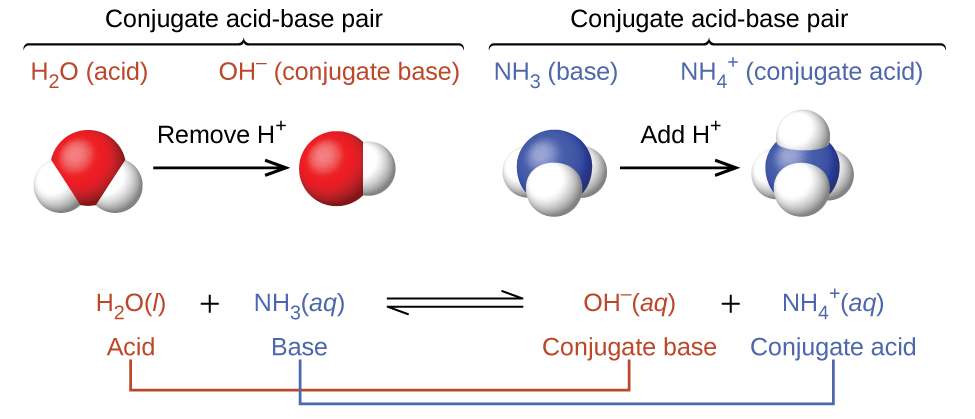
The reaction between a Brønsted-Lowry acid and water is called acid ionization. For example, when hydrogen fluoride dissolves in water and ionizes, protons are transferred from hydrogen fluoride molecules to water molecules, yielding hydronium ions and fluoride ions:

When we add a base to water, a base ionization reaction occurs in which protons are transferred from water molecules to base molecules. For example, adding pyridine to water yields hydroxide ions and pyridinium ions:
Notice that both these ionization reactions are represented as equilibrium processes. The relative extent to which these acid and base ionization reactions proceed is an important topic treated in a later section of this chapter. In the preceding paragraphs we saw that water can function as either an acid or a base, depending on the nature of the solute dissolved in it. In fact, in pure water or in any aqueous solution, water acts both as an acid and a base. A very small fraction of water molecules donate protons to other water molecules to form hydronium ions and hydroxide ions:
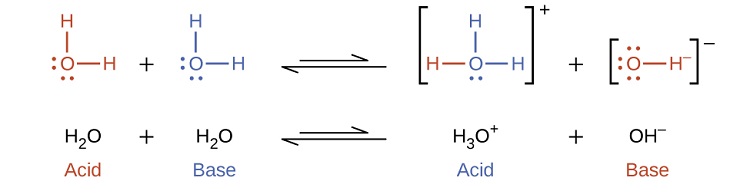
This type of reaction, in which a substance ionizes when one molecule of the substance reacts with another molecule of the same substance, is referred to as autoionization. Pure water undergoes autoionization to a very slight extent. Only about two out of every \(10^9\) molecules in a sample of pure water are ionized at 25 °C. The equilibrium constant for the ionization of water is called the ion-product constant for water (Kw):
\[\ce{H_2O}_{(l)}+\ce{H_2O}_{(l)} \rightleftharpoons \ce{H_3O^+}_{(aq)}+\ce{OH^-}_{(aq)}\;\;\; K_\ce{w}=\ce{[H_3O^+][OH^- ]} \label{14.14} \]
The slight ionization of pure water is reflected in the small value of the equilibrium constant; at 25 °C, Kw has a value of \(1.0 \times 10^{−14}\). The process is endothermic, and so the extent of ionization and the resulting concentrations of hydronium ion and hydroxide ion increase with temperature. For example, at 100 °C, the value for \(K_\ce{w}\) is approximately \(5.1 \times 10^{−13}\), roughly 50-times larger than the value at 25 °C.
What are the hydronium ion concentration and the hydroxide ion concentration in pure water at 25 °C?
Solution
The autoionization of water yields the same number of hydronium and hydroxide ions. Therefore, in pure water, \(\ce{[H_3O^+]} = \ce{[OH^- ]}\). At 25 °C:
\[K_\ce{w}=\ce{[H_3O^+][OH^- ]}=\ce{[H_3O^+]^2}=\ce{[OH^- ]^2}=1.0 \times 10^{−14} \nonumber \]
So:
\[\ce{[H_3O^+]}=\ce{[OH^- ]}=\sqrt{1.0 \times 10^{−14}} =1.0 \times 10^{−7}\; M \nonumber \]
The hydronium ion concentration and the hydroxide ion concentration are the same, and we find that both equal \(1.0 \times 10^{−7}\; M\).
The ion product of water at 80 °C is \(2.4 \times 10^{−13}\). What are the concentrations of hydronium and hydroxide ions in pure water at 80 °C?
- Answer
-
\(\ce{[H_3O^+]} = \ce{[OH^- ]} = 4.9 \times 10^{−7}\; M\)
It is important to realize that the autoionization equilibrium for water is established in all aqueous solutions. Adding an acid or base to water will not change the position of the equilibrium. Example 14.12 demonstrates the quantitative aspects of this relation between hydronium and hydroxide ion concentrations.
The Inverse Proportionality of [H3O+] and [OH-] A solution of carbon dioxide in water has a hydronium ion concentration of \(2.0 \times 10^{−6}\; M\). What is the concentration of hydroxide ion at 25 °C?
Solution
We know the value of the ion-product constant for water at 25 °C:
\[\ce{2 H_2O}_{(l)} \rightleftharpoons \ce{H_3O^+}_{(aq)} + \ce{OH^-}_{(aq)} \nonumber \]
\[K_\ce{w}=\ce{[H3O+][OH^- ]}=1.0 \times 10^{−14} \nonumber \]
Thus, we can calculate the missing equilibrium concentration.
Rearrangement of the Kw expression yields that \([\ce{OH^- }]\) is directly proportional to the inverse of [H3O+]:
\[[\ce{OH^- }]=\dfrac{K_{\ce w}}{[\ce{H_3O^+}]}=\dfrac{1.0 \times 10^{−14}}{2.0 \times 10^{−6}}=5.0 \times 10^{−9} \nonumber \]
The hydroxide ion concentration in water is reduced to \(5.0 \times 10^{−9}\: M\) as the hydrogen ion concentration increases to \(2.0 \times 10^{−6}\; M\). This is expected from Le Chatelier’s principle; the autoionization reaction shifts to the left to reduce the stress of the increased hydronium ion concentration and the \(\ce{[OH^- ]}\) is reduced relative to that in pure water.
A check of these concentrations confirms that our arithmetic is correct:
\[\begin{align*} K_\ce{w} &=\ce{[H_3O^+][OH^- ]} \\[4pt] &=(2.0 \times 10^{−6})(5.0 \times 10^{−9})\\[4pt] &=1.0 \times 10^{−14} \end{align*} \nonumber \]
What is the hydronium ion concentration in an aqueous solution with a hydroxide ion concentration of 0.001 M at 25 °C?
- Answer
-
\[\ce{[H3O+]} = 1 \times 10^{−11} M \nonumber \]
Amphiprotic Species
Like water, many molecules and ions may either gain or lose a proton under the appropriate conditions. Such species are said to be amphiprotic. Another term used to describe such species is amphoteric, which is a more general term for a species that may act either as an acid or a base by any definition (not just the Brønsted-Lowry one). Consider for example the bicarbonate ion, which may either donate or accept a proton as shown here:
\[\ce{HCO^-}_{3(aq)} + \ce{H_2O}_{(l)} \rightleftharpoons \ce{CO^{2-}}_{3(aq)} + \ce{H_3O^+}_{(aq)} \label{14.15a} \]
\[ \ce{HCO^-}_{3(aq)} + \ce{H_2O}_{(l)} \rightleftharpoons \ce{H_2CO}_{3(aq)} + \ce{OH^-}_{(aq)} \label{14.15b} \]
Write separate equations representing the reaction of \(\ce{HSO3-}\)
- as an acid with \(\ce{OH^-}\)
- as a base with HI
Solution
- \(\ce{HSO3-}(aq)+ \ce{OH^-}(aq)\rightleftharpoons \ce{SO3^2-}(aq)+ \ce{H_2O}_{(l)} \)
- \(\ce{HSO3-}(aq)+\ce{HI}(aq)\rightleftharpoons \ce{H2SO3}(aq)+\ce{I-}(aq)\)
Write separate equations representing the reaction of \(\ce{H2PO4-}\)
- as a base with HBr
- as an acid with \(\ce{OH^-}\)
- Answer a
-
\(\ce{H2PO4-}(aq)+\ce{HBr}(aq)\rightleftharpoons \ce{H3PO4}(aq)+\ce{Br-}(aq)\)
- Answer b
-
\(\ce{H2PO4-}(aq)+\ce{OH^-} (aq)\rightleftharpoons \ce{HPO4^2-}(aq)+ \ce{H_2O}_{(l)} \)
Summary
A compound that can donate a proton (a hydrogen ion) to another compound is called a Brønsted-Lowry acid. The compound that accepts the proton is called a Brønsted-Lowry base. The species remaining after a Brønsted-Lowry acid has lost a proton is the conjugate base of the acid. The species formed when a Brønsted-Lowry base gains a proton is the conjugate acid of the base. Thus, an acid-base reaction occurs when a proton is transferred from an acid to a base, with formation of the conjugate base of the reactant acid and formation of the conjugate acid of the reactant base. Amphiprotic species can act as both proton donors and proton acceptors. Water is the most important amphiprotic species. It can form both the hydronium ion, H3O+, and the hydroxide ion, \(\ce{OH^-}\) when it undergoes autoionization:
\[\ce{2 H_2O}_{(l)} \rightleftharpoons \ce{H_3O^+}(aq)+\ce{OH^-} (aq) \nonumber \]
The ion product of water, Kw is the equilibrium constant for the autoionization reaction:
\[K_\ce{w}=\mathrm{[H_3O^+][OH^- ]=1.0 \times 10^{−14} \; at\; 25°C} \nonumber \]
Key Equations
- \[K_{\ce w} = \ce{[H3O+][OH^- ]} = 1.0 \times 10^{−14}\textrm{ (at 25 °C)} \nonumber \]
Glossary
- acid ionization
- reaction involving the transfer of a proton from an acid to water, yielding hydronium ions and the conjugate base of the acid
- amphiprotic
- species that may either gain or lose a proton in a reaction
- amphoteric
- species that can act as either an acid or a base
- autoionization
- reaction between identical species yielding ionic products; for water, this reaction involves transfer of protons to yield hydronium and hydroxide ions
- base ionization
- reaction involving the transfer of a proton from water to a base, yielding hydroxide ions and the conjugate acid of the base
- Brønsted-Lowry acid
- proton donor
- Brønsted-Lowry base
- proton acceptor
- conjugate acid
- substance formed when a base gains a proton
- conjugate base
- substance formed when an acid loses a proton
- ion-product constant for water (Kw)
- equilibrium constant for the autoionization of water


