13.3: The Equilibrium Constant

The constancy of the ratio of the equilibrium concentration of one isomer to the concentration of the other at a given temperature is characteristic of all gaseous equilibria between isomers, i.e.,of all reactions of the general type

\[\text{A}\text{ }({g})\rightleftharpoons \text{B}\text{ }({g})\label{1} \]

The constant ratio of concentrations is called the equilibrium constant and is given the symbol \(K_c\). For reactions of the type given by Equation \(\ref{1}\) the equilibrium constant is thus described by the equation

\[K_{c}=\frac{[\text{ B }]}{[\text{ A }]}\label{2} \]

where, by convention, the concentration of the product B appears in the numerator of the ratio. If, for some reason, we wish to look at this reaction in reverse,

\[\text{B}\text{ }({g})\rightleftharpoons \text{A}\text{ }({g}) \nonumber \]

then the equilibrium constant is denoted as the reciprocal of the constant given in Equation \(\ref{2}\).

\[K_{c}=\frac{[\text{ A }]}{[\text{ B }]} \nonumber \]

In general the equilibrium constant \(K_c\) varies with temperature and also differs based on the substances involved. Examples illustrating this behavior are given in Table \(\PageIndex{1}\) where the experimentally determined equilibrium constants for various cis-trans isomerization equilibria are recorded at various temperatures. Note that the equilibrium changes as the temperature and the composition of the molecule changes.

TABLE \(\PageIndex{1}\) The Equilibrium Constant K_c for some Cis-Trans Interconversions.

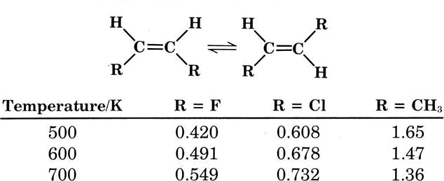
When we turn our attention to more complex equilibrium reactions, we find that the relationship between the concentrations of the various species is no longer a simple ratio. A good demonstration of this fact is provided by the dissociation of dinitrogen tetroxide, N₂O₄. This compound is a colorless gas, but even at room temperature it dissociates partly into a vivid red-brown gas, NO₂, according to the equation

\[\text{N}_{2}\text{O}_{4}\text{ }({g})\rightleftharpoons \text{2NO}_{2} \text{ }({g})\label{5} \]

If 1 mol N₂O₄ contained in a flask of volume 1 L is heated to 407.2 K, exactly one-half of it dissociates into NO₂. If the volume is now increased, the ratio of [NO₂] to [N₂O₄] does not remain constant but increases as more dissociates. As shown in Table \(\PageIndex{2}\) , if we increase the volume still further, even more dissociation occurs. By the time we have increased the volume to 10 L, the fraction of N₂O₄ molecules dissociated has increased to 0.854 (i.e., to 85.4 percent).

Obviously the situation is now not quite so straightforward as in the previous example. Nevertheless there is a simple relationship between the equilibrium concentrations of the reactant and product in this case too. We find that it is the quantity

\[\frac{[\text{ NO}_{2}]^{2}}{[\text{ N}_{2}\text{O}_{4}]} \nonumber \]

rather than the simple ratio of concentrations, which is now constant. Accordingly we also call this quantity an equilibrium constant and give it the symbol K_c. Thus K_c for Equation \(\ref{5}\) is given by the relationship

\[K_{c}=\frac{[\text{ NO}_{2}]^{2}}{[\text{ N}_{2}\text{O}_{4}]} \nonumber \]

where again by convention the product appears in the numerator. It is easy to check that K_c actually is a constant quantity with the value 2.00 mol/L from the data given in Table \(\PageIndex{2}\) . Thus if we take the result from line d, we find that when 1 mol N₂O₄ is placed in a 10 L flask at 407 K, 0.854 mol dissociate.

TABLE \(\PageIndex{2}\) The Dissociation of 1 mol \(N_2O_4\) into NO2 at 407.2 K (134°C) and Various Volumes.

	Amount of N2O4 Added mol	Volume of Flask L	Fraction N2O4 Dissociated	Amount N2O4 at Equilibrium mol	Amount NO2 at Equilibrium mol	Concentration N2O4 at Equilibrium mol/L	Concentration NO2 at Equilibrium mol/L	Equilibrium Constant Kc mol/L
a	1	1	0.500	0.500	1.000	0.500	1.000	2.000
b	1	2	0.618	0.382	1.236	0.191	0.618	2.000
c	1	5	0.766	0.234	1.532	0.0468	0.3064	2.006
d	1	10	0.854	0.146	1.708	0.0146	0.1708	1.998

Since from Equation \(\ref{5}\) each mole which dissociates yields 2 mol NO₂,there will be

\[\text{0.854 mol N}_{2}\text{O}_{4}\times \frac{\text{2 mol NO}_{2}}{\text{1 mol N}_{2}\text{O}_{4}}=\text{1.708 mol NO}_{2} \nonumber \]

present in the reaction vessel. There will also be (1 – 0.854) mol = 0.146 mol N₂O₄ left undissociated in the flask. Since the total volume is 10 L, the equilibrium concentrations are

\[[\text{ NO}_{2}]=\frac{\text{1.708 mol}}{\text{10 L}}=\text{0.1708 mol/L} \nonumber \]

and

\[[\text{ N}_{2}\text{O}_{4}]=\frac{\text{0.146 mol}}{\text{10 L}}=\text{0.0146 mol/L} \nonumber \]

Accordingly

\[K_{c}=\frac{\text{1.708 mol/L}\times \text{ 0.1708 mol/L}}{\text{0.0146 mol/L}}=\text{2.00 mol/L} \nonumber \]

In exactly the same way, if we use the data from line a in Table \(\PageIndex{2}\) , we find

\[K_{c}=\frac{[\text{ NO}_{2}]^{2}}{[\text{ N}_{2}\text{O}_{4}]}=\frac{\text{(1.00 mol/L}\text{)}^{2}}{\text{0.5 mol/L}}=\text{2.00 mol/L} \nonumber \]

You can check for yourself that lines b and c also yield the same value forK_c.

Example \(\PageIndex{1}\) : Equilibrium Constant

When 2 mol N₂O₄ gas is heated to 407 K in a vessel of volume 5 dm³, it is found that 0.656 of the molecules dissociate into NO₂. Show that these data are in agreement with the value for K_c of 2.00 mol dm^–3 given in the text.

Solution

Many equilibrium problems can be solved in a fairly standardized fashion in three stages.

a) Calculate the amount of each substance transformed by the reaction as it comes to equilibrium, i.e., the amount of each reactant consumed by the reaction and the amount of each product produced by the reaction. Stoichiometric ratios derived from the equation must always be used in these calculations.

In this particular example we note that 0.656 of the original N₂O₄ dissociates. Since 2 mol was used, a total of 0.656 × 2 = 1.312 mol N₂O₄ is consumed. The amount of NO₂ produced is accordingly

\(n_{\text{NO}_{2}}=\text{1.312 mol N}_{2}\text{O}_{4}\times \dfrac{\text{2 mol NO}_{2}}{\text{1 mol N}_{2}\text{O}_{4}}=\text{2.624 mol NO}_{2}\)

b) Use the amounts calculated in the first stage to calculate the amount of each substance present at equilibrium. Dividing by the volume, we can obtain the equilibrium concentrations.

Since 1.312 mol N₂O₄ dissociated out of an original 2 mol, we have (2 – 1.312) mol = 0.688 mol N₂O₄ left. The equilibrium concentration of N₂O₄ is thus

\([\text{ N}_{2}\text{O}_{4}] = \dfrac{0.688\text{ mol N}_{2}\text{O}_{4}}{\text{ 5.00 dm}^{3}} = \text{0.1376 mol dm}^{-3}\)

Since no NO₂ was originally present, the amount of NO₂ present at equilibrium is the amount produced by the dissociation, namely, 2.624 mol NO₂. Thus

\([\text{ NO}_{2}]=\dfrac{\text{2.624 mol NO}_{2}}{\text{5.00 dm}^{3}}=\text{0.525 mol dm}^{-3}\)

It is usually worthwhile tabulating these calculations, particularly in more complex examples.

Note that a negative quantity in the column headed Amount Produced indicates that a given substance (such as N₂O₄ in this example) has been consumed. There is less of that substance when equilibrium is reached than was present initially.

Substance	Initial Amount mol	Amount Produced mol	Equilibrium Amount mol	Equilibrium Concentration mol dm^-3
N2O4	2.00	-1.312	0.688	0.688/5
NO2	0.00	2.624	2.624	2.624/5

c) In the third stage we insert the equilibrium concentrations in an expression for the equilibrium constant:

\(K_{c}=\dfrac{[\text{ NO}_{2}]^{2}}{[\text{ N}_{2}\text{O}_{4}]}=\dfrac{\text{0.525 mol dm}^{-3}\times \text{ 0.525 mol dm}^{-3}}{\text{0.1376 mol dm}^{-3}}=\text{2.00 mol dm}^{-3}\)