3.10: Standard Enthalpies of Formation
- Page ID
- 49282
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By now chemists have measured the enthalpy changes for so many reactions that it would take several large volumes to list all the thermochemical equations. Fortunately Hess' law makes it possible to list a single value, the standard enthalpy of formation ΔHf, for each compound. The standard enthalpy of formation is the enthalpy change when 1 mol of a pure substance is formed from its elements. Each element must be in the physical and chemical form which is most stable at normal atmospheric pressure and a specified temperature (usually 25°C).
For example, if we know that \[ \Delta H_{f} [ \text{H}_{2} \text{O} (l) ] = –285.8 \text{ kJ } \text{mol}^{-1} \nonumber \], we can immediately write the thermochemical equation
\[ \text{H}_{2} (g) + \frac{1}{2} \text{O}_{2} (g) \rightarrow \text{H}_{2} \text{O} (l) ~~~~~~~~~~~~ \Delta H_{m} = –285.8 \text{ kJ} \text{mol}^{-1} \label{1} \]
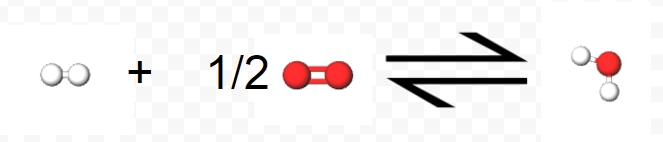

The elements H and O appear as diatomic molecules and in gaseous form because these are their most stable chemical and physical states. Note also that 285.8 kJ are given off per mole of H2O(l) formed. Equation \(\ref{1}\) must specify formation of 1 mol H2O(l), and so the coefficient of O2 must be ½. Note the 3 different views of this reaction, the equation providing a symbolic view, the 3D molecules providing a microscopic view, and the photos providing a macroscopic view of the reaction as we would see it with our own 2 eyes.
In some cases, such as that of water, the elements will react directly to form a compound, and measurement of the heat absorbed serves to determine ΔHf. Quite often, however, elements do not react directly with each other to form the desired compound, and ΔHf must be calculated by combining the enthalpy changes for other reactions. A case in point is the gas acetylene, C2H2. In Example 1 from the Hess' law section we showed that the thermochemical equation
\[2 \text{C} (s) + \text{H}_{2} (g) \rightarrow \text{C}_{2} \text{H}_{2} (g) ~~~~~~~~~ \Delta H_{m} = 227.0 \text{ kJ } \text{mol}^{-1} \nonumber \]
was valid. Since it involves 1 mol C2H2 and the elements are in their most stable forms, we can say that ΔHf[C2H2(g)] = 227.0 kJ mol–1.
One further point arises from the definition of ΔHf. The standard enthalpy of formation for an element in its most stable state must be zero. If we form mercury from its elements, for example, we are talking about the reaction
\[ \text{Hg} (l) \rightarrow \text{Hg} (l) \nonumber \]
Since the mercury is unchanged, there can be no enthalpy change, and \[ \Delta H_{f} = 0 \text{ kJ} \text{ mol}^{-1} \nonumber \].
| Compound |
ΔHf/kJ mol–1 |
ΔHf/kcal mol–1 |
Compound |
ΔHf/kJ mol–1 |
ΔHf/kcal mol–1 |
|---|---|---|---|---|---|
| AgCl(s) |
–127.068
|
–30.35
|
H2O(g) |
–241.818
|
–57.79
|
| AgN3(s) |
+620.6
|
+148.3
|
H2O(l) |
–285.8
|
–68.3
|
| Ag2O(s) |
–31.0
|
–7.41
|
H2O2(l) |
–187.78
|
–44.86
|
| Al2O3(s) |
–1675.7
|
–400.40
|
H2S(g) |
–20.63
|
–4.93
|
| Br2(l) |
0.0
|
0.00
|
HgO(s) |
–90.83
|
–21.70
|
| Br2(g) |
+30.907
|
+7.385
|
I2(s) |
0.0
|
0.0
|
| C(s), graphite |
0.0
|
0.00
|
I2(g) |
+62.438
|
+14.92
|
| C(s), diamond |
+1.895
|
+0.453
|
KCl(s) |
–436.747
|
–104.36
|
| CH4(g) |
–74.81
|
–17.88
|
KBr(s) |
–393.798
|
–94.097
|
| CO(g) |
–110.525
|
–26.41
|
MgO(s) |
–601.7
|
–143.77
|
| CO2(g) |
–393.509
|
–94.05
|
NH3(g) |
–46.11
|
–11.02
|
| C2H2(g) |
+226.73
|
+54.18
|
NO(g) |
+90.25
|
+21.57
|
| C2H4(g) |
+52.26
|
+12.49
|
NO2(g) |
+33.18
|
+7.93
|
| C2H6(g) |
–84.68
|
–20.23
|
N2O4(g) |
+9.16
|
+2.19
|
| C6H6(l) |
+49.03
|
+11.72
|
NF3(g) |
–124.7
|
–29.80
|
| CaO(s) |
–635.09
|
–151.75
|
NaBr(s) |
–361.062
|
–86.28
|
| CaCO3(s) |
–1206.92
|
–288.39
|
NaCl(s) |
–411.153
|
–98.24
|
| CuO(s) |
–157.3
|
–37.59
|
O3(g) |
+142.7
|
+34.11
|
| Fe2O3(s) |
–824.2
|
–196.9
|
SO2(g) |
–296.83
|
–70.93
|
| HBr(g) |
–36.4
|
–8.70
|
SO3(g) |
–395.72
|
–94.56
|
| HCl(g) |
–92.307
|
–22.06
|
ZnO(s) |
–348.28
|
–83.22
|
| HI(g) |
+26.48
|
+6.33
|
Standard enthalpies of formation for some common compounds are given in Table \(\PageIndex{1}\). These values may be used to calculate ΔHm for any chemical reaction so long as all the compounds involved appear in the tables. To see how and why this may be done, consider the following example.
Use standard enthalpies of formation to calculate ΔHm for the reaction
\[ 2 \text{CO} (g) + \text{O}_{2} (g) \rightarrow 2 \text{C} \text{O}_{2} (g) \nonumber \]
Solution:
We can imagine that the reaction takes place in two steps, each of which involves only a standard enthalpy of formation. In the first step CO (carbon monoxide) is decomposed to its elements:
\[ 2 \text{CO} (g) \rightarrow 2 \text{C} (s) + \text{O}_{2} (g) ~~~~~~~~~~ \Delta H_{m} = \Delta H_{1}\label{2} \]
Since this is the reverse of formation of 2 mol CO from its elements, the enthalpy change is
\[ \Delta H_{1} = 2 \times { – \Delta H_{f} [ \text{CO} (g) ] } = 2 \times [ – ( – 110.5 \text{ kJ} \text{ mol}^{-1} ) ] = +221.0 \text{ kJ} \text{ mol}^{-1} \nonumber \]
In the second step the elements are combined to give 2 mol CO2(carbon dioxide):
\[ 2 \text{C} (s) + 2 \text{O}_{2} (g) \rightarrow 2 \text{C} \text{O}_{2} (g) ~~~~~~~~~ \Delta H_{m} = \Delta H_{2} \label{3} \]
In this case
\[ \Delta H_{2} = 2 \times \Delta H_{f} [ \text{C} \text{O}_{2} (g)] = 2 \times (– 393.5 \text{ kJ } \text{mol}^{-1}) = – 787.0 \text{ kJ } \text{mol}^{-1} \nonumber \]
You can easily verify that the sum of Equations \(\ref{2}\) and \(\ref{3}\) is
\[ 2 \text{CO} (g) + 2 \text{O}_{2} (g) \rightarrow 2 \text{C} \text{O}_{2} (g) ~~~~~~~~~~~ \Delta H_{m} = \Delta H_{net} \nonumber \]
Therefore
\[ \Delta H_{net} = \Delta H_{1} + \Delta H_{2} = 221.0 \text{ kJ } \text{mol}^{-1} – 787.0 \text{mol}^{-1} = – 566.0 \text{mol}^{-1} \nonumber \]
Note carefully how Example \(\PageIndex{1}\) was solved. In step 1 the reactant compound CO(g) was hypothetically decomposed to its elements. This equation was the reverse of formation of the compound, and so ΔH1 was opposite in sign from ΔHf. Step 1 also involved 2 mol CO(g) and so the enthalpy change had to be doubled. In step 2 we had the hypothetical formation of the product CO2(g) from its elements. Since 2 mol were obtained, the enthalpy change was doubled but its sign remained the same.
Any chemical reaction can be approached similarly. To calculate ΔHm we add all the ΔHf values for the products, multiplying each by the appropriate coefficient, as in step 2 above. Since the signs of ΔHf for the reactants had to be reversed in step 1, we subtract them, again multiplying by appropriate coefficients. This can he summarized by the equation
\[ \Delta H_{m} = \sum \Delta H_{f} \text{ (products)} – \sum \Delta H_{f} \text{ (reactants)} \label{4} \]
The symbol Σ means “the sum of.” Since ΔHf values are given per mole of compound, you must be sure to multiply each ΔHf by an appropriate coefficient derived from the equation for which ΔHm is being calculated.
Use the table of standard enthalpies of formation at 25°C to calculate ΔHm for the reaction
\[ 4 \text{N} \text{H}_{3} (g) + 5 \text{O}_{2} (g) \rightarrow 6 \text{H}_{2} \text{O} (g) + 4 \text{NO} (g) \nonumber \]
Solution
Using Equation \(\ref{4}\), we have
\[ \begin{align} \Delta H_{m} & = \sum \Delta H_{f} \text{ (products)} – \sum \Delta H_{f} \text{ (reactants)} \\ & = [ 6 \Delta H_{f} ( \text{H}_{2} \text{O} ) + 4 \Delta H_{f} \text{(NO)]} – [4 \Delta H_{f} \text{ (N} \text{H}_{3} ) + 5 \Delta H_{f} \text{ (O}_{2} )] \\ & = 6 ( – 241.8) \text{ kJ} \text{ mol}^{-1} + 4 ( 90.3 ) \text{ kJ} \text{ mol}^{-1} – 4(–46.1 \text{ kJ} \text{ mol}^{-1} ) – 5 \times 0 \\ & = –1450.8 \text{ kJ} \text{ mol}^{-1} + 361.2 \text{ kJ} \text{ mol}^{-1} + 184.4 \text{ kJ} \text{ mol}^{-1} \\ & = –905.2 \text{ kJ} \text{ mol}^{-1} \end{align} \nonumber \]
Note that we were careful to use ΔHf [H2O(g)] not ΔHf [H2O(l)]. Even though water vapor is not the most stable form of water at 25°C, we can still use its ΔHf value. Also the standard enthalpy of formation of the element O2(g) is zero by definition. Obviously it would be a waste of space to include it in the table above.


