11.5: Equilibrium Calculations
- Page ID
- 3528
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The five Examples presented above were carefully selected to span the range of problem types that students enrolled in first-year college chemistry courses are expected to be able to deal with. If you are able to reproduce these solutions on your own, you should be well prepared on this topic.
- The first step in the solution of all but the simplest equilibrium problems is to sketch out a table showing for each component the initial concentration or pressure, the change in this quantity (for example, +2x), and the equilibrium values (for example, .0036 + 2x). In doing so, the sequence of calculations required to get to the answer usually becomes apparent.
- Equilibrium calculations often involve quadratic- or higher-order equations. Because concentrations, pressures, and equilibrium constants are seldom known to a precision of more than a few significant figures, there is no need to seek exact solutions. Iterative approximations (as in Example \(\PageIndex{3}\)) or use of a graphical calculator (Example \(\PageIndex{4}\)) are adequate and convenient.
- Phase distribution equilibria play an important role in chemical separation processes on both laboratory and industrial scales. They are also involved in the movement of chemicals between different parts of the environment, and in the bioconcentration of pollutants in the food chain.
This page presents examples that cover most of the kinds of equilibrium problems you are likely to encounter in a first-year university course. Reading this page will not teach you how to work equilibrium problems! The only one who can teach you how to interpret, understand, and solve problems is yourself. So don't just "read" this and think you are finished. You need to find and solve similar problems on your own. Look over the problems in your homework assignment or at the end of the appropriate chapter in a textbook, and see how they fit into the general types described below. When you can solve them without looking at the examples below, you will be well on your way!
Calculating Equilibrium Constants
Clearly, if the concentrations or pressures of all the components of a reaction are known, then the value of \(K\) can be found by simple substitution. Observing individual concentrations or partial pressures directly may be not always be practical, however. If one of the components is colored, the extent to which it absorbs light of an appropriate wavelength may serve as an index of its concentration. Pressure measurements are ordinarily able to measure only the total pressure of a gaseous mixture, so if two or more gaseous products are present in the equilibrium mixture, the partial pressure of one may need to be inferred from that of the other, taking into account the stoichiometry of the reaction.
In an experiment carried out by Taylor and Krist (J. Am. Chem. Soc. 1941: 1377), hydrogen iodide was found to be 22.3% dissociated at 730.8 K. Calculate \(K_c\) for
\[\ce{ 2 HI(g) <=> H2(g) + I2} \nonumber \]
Solution
No explicit molar concentrations are given, but we do know that for every \(n\) moles of \(\ce{HI}\), \(0.223n\) moles of each product is formed and \((1–0.223)n = 0.777n\) moles of \(\ce{HI}\) remains. For simplicity, we assume that \(n=1\) and that the reaction is carried out in a 1.00-L vessel, so that we can substitute the required concentration terms directly into the equilibrium expression for \(K_c\).
\[\begin{align*} K_c &= \dfrac{[\ce{H2}][\ce{I2}]}{[\ce{HI}]^2} \\[4pt] &= \dfrac{(0.223)(0.223)}{(0.777)^2} \\[4pt] &= 0.082 \end{align*}\]
Ordinary white phosphorus, \(\ce{P4}\), forms a vapor which dissociates into diatomic molecules at high temperatures:
\[\ce{P4(g) <=> 2 P2(g)} \nonumber\]
A sample of white phosphorus, when heated to 1000°C, formed a vapor having a total pressure of 0.20 atm and a density of 0.152 g L–1. Use this information to evaluate the equilibrium constant \(K_p\) for this reaction.
Solution
Before worrying about what the density of the gas mixture has to do with \(K_p\), start out in the usual way by laying out the information required to express \(K_p\) in terms of an unknown \(x\)
| ICE Table | \(P_{4(g)}\) | \(P_{2(g)}\) | comment |
|---|---|---|---|
| Initial (moles) | 1 | 0 | Since \(K\) is independent of the number of moles, assume the simplest initial case. |
| Change (moles) | \(-x\) | \(2x\) | x is the fraction of P4 that dissociates. |
| Equilibrium (moles) | \(1-x\) | \(2x\) | The denominator is the total number of moles: |
| Mole Fraction | \(\chi_{P_4}=\dfrac{1-x}{1+x}\) | \(\chi_{P_2}=\dfrac{2x}{1+x}\) | The denominator is the total number of moles: |
| Equilibrium (pressures) |
\(p_{P_4} = \chi_{P_4} 0.2 = \left( \dfrac{1-x}{1+x}\right) 0.2 \) | \(p_{P_2} = \chi_{P_2} 0.2 = \left( \dfrac{2x}{1+x}\right) 0.2 \) | Partial pressure is the mole fraction times the total pressure. |
The partial pressures in the bottom row were found by multiplying the mole fraction of each gas by the total pressure:
\[P_i = \chi_i P_{tot} \nonumber\]
with the term in the denominator of each mole fraction is the total number of moles of gas present at equilibrium:
\[P_{tot} = 1-x + 2x = 1+x \nonumber\]
Expressing the equilibrium constant in terms of \(x\) gives
\[ \begin{align*} K_p &= \dfrac{p^2_{P_2}}{p_{P_4}} \\[4pt] &= \dfrac{\left(\dfrac{2x}{1+x}\right)^2 0.2^2} {\left(\dfrac{1-x}{1+x}\right) 0.2} \\[4pt] &= \left(\dfrac{4x^2}{(1-x)(1+x)}\right) 0.2 \\[4pt] &= \left(\dfrac{4x^2}{1+x^2}\right) 0.2 \end{align*}\]
Now we need to find the dissociation fraction \(x\) of \(P_4\), and at this point we hope you remember those gas laws that you were told you would be needing later in the course! The density of a gas is directly proportional to its molecular weight, so you need to calculate the densities of pure \(P_4\) and pure \(P_2\) vapors under the conditions of the experiment. One of these densities will be greater than 0.152 gL–1 and the other will be smaller; all you need to do is to find where the measured density falls in between the two limits, and you will have the dissociation fraction.
The molecular weight of phosphorus is 31.97, giving a molar mass of 127.9 g for \(\ce{P4}\). This mass must be divided by the volume to find the density; assuming ideal gas behavior, the volume of 127.9 g (1 mole) of \(\ce{P4}\) is given by RT/P, which works out to 522 L (remember to use the absolute temperature here.) The density of pure \(\ce{P4}\) vapor under the conditions of the experiment is then
\[\rho = \dfrac{m}{V} = (128\; g \;mol^{–1}) \times x = (522\; L mol^{–1}) = 0.245\; g\; L^{–1} \nonumber\]
The density of pure \(P_2\) would be half this, or 0.122 g L–1. The difference between these two limiting densities is 0.123 g L–1, and the difference between the density of pure \(\ce{P4}\) and that of the equilibrium mixture is (0.245 – 0.152) g L–1 or 0.093 g L–1. The ratio 0.093/0.123 = 0.76 is therefore the fraction of \(\ce{P4}\) that remains and its fractional dissociation is (1 – 0.76) = 0.24. Substituting into the equilibrium expression above gives \(K_p = 1.2\).
Solve Example \(\PageIndex{2}\) by using a different set of initial conditions to demonstrated that the initial conditions indeed have no effect on determining the Equilibrium state and \(K_p\).
Calculating Equilibrium Concentrations
This is by far the most common kind of equilibrium problem you will encounter: starting with an arbitrary number of moles of each component, how many moles of each will be present when the system comes to equilibrium? The principal source of confusion and error for beginners relates to the need to determine the values of several unknowns (a concentration or pressure for each component) from a single equation, the equilibrium expression. The key to this is to make use of the stoichiometric relationships between the various components, which usually allow us to express the equilibrium composition in terms of a single variable. The easiest and most error-free way of doing this is adopt a systematic approach in which you create and fill in a small table as shown in the following problem example. You then substitute the equilibrium values into the equilibrium constant expression, and solve it for the unknown.
This very often involves solving a quadratic or higher-order equation. Quadratics can of course be solved by using the familiar quadratic formula, but it is often easier to use an algebraic or graphical approximation, and for higher-order equations this is the only practical approach. There is almost never any need to get an exact answer, since the equilibrium constants you start with are rarely known all that precisely anyway.
Phosgene (\(\ce{COCl2}\)) is a poisonous gas that dissociates at high temperature into two other poisonous gases, carbon monoxide and chlorine. The equilibrium constant Kp = 0.0041 at 600°K. Find the equilibrium composition of the system after 0.124 atm of \(\ce{COCl2}\) is allowed to reach equilibrium at this temperature.
Solution
First we need a balanced chemical reaction
\[\ce{COCl_2 <=> CO(g) + Cl2(g)} \nonumber\]
Start by drawing up a table showing the relationships between the components:
| ICE Table | \(COCl_2\) | \(CO_{(g)}\) | \(Cl_{2(g)}\) |
|---|---|---|---|
| Initial (pressure) | 0.124 atm | 0 | 0 |
| Change (pressure) | -x | +x | +x |
| Equilibrium (pressure) | 0.124 – x | +x | +x |
Substitution of the equilibrium pressures into the equilibrium expression gives
\[ \dfrac{x^2}{0.124 - x} = 0.0041 \nonumber\]
This expression can be rearranged into standard polynomial form
\[x^2 +0.0041 x – 0.00054 = 0 \nonumber\]
and solved by the quadratic formula, but we will simply obtain an approximate solution by iteration. Because the equilibrium constant is small, we know that x will be rather small compared to 0.124, so the above relation can be approximated by
\[ \dfrac{x^2}{0.124 - x} \approx \dfrac{x^2}{0.124}= 0.0041 \nonumber\]
which gives x = 0.0225. To see how good this is, substitute this value of x into the denominator of the original equation and solve again:
\[ \dfrac{x^2}{0.124 - 0.0225} = \dfrac{x^2}{0.102}= 0.0041 \nonumber\]
This time, solving for \(x\) gives 0.0204. Iterating once more, we get
\[ \dfrac{x^2}{0.124 - 0.0204} = \dfrac{x^2}{0.104}= 0.0041 \nonumber\]
and x = 0.0206 which is sufficiently close to the previous to be considered the final result. The final partial pressures are then 0.104 atm for COCl2, and 0.0206 atm each for CO and Cl2.
Comment: Using the quadratic formula to find the exact solution yields the two roots –0.0247 (which we ignore) and 0.0206, which show that our approximation is quite good.
The gas-phase dissociation of phosphorus pentachloride to the trichloride has \(K_p = 3.60\) at 540°C:
\[\ce{PCl5(g) <=> PCl3(g) + Cl2(g)} \nonumber\]
What will be the partial pressures of all three components if 0.200 mole of \(\ce{PCl5}\) and 3.00 moles of \(\ce{PCl3}\) are combined and brought to equilibrium at this temperature and at a total pressure of 1.00 atm?
Solution
As always, set up a table showing what you know (first two rows) and then expressing the equilibrium quantities:
| ICE Table | \(\ce{PC5(g)}\) | \(\ce{PCl3(g)}\) | \(\ce{Cl2(g)}\) |
|---|---|---|---|
| Initial (moles) | 0.200 | 3.00 | 0 |
| Change (moles) | –x | +x | +x |
| Equilibrium (moles) | 0.200 – x | 3.00 + x | x |
| Equilibrium (partial pressures) | \(\dfrac{2.00 - x }{ 3.20 + x}\) | \(\dfrac{3.00 + x }{ 3.20 + x}\) | \(\dfrac{ x }{ 3.20 + x}\) |
The partial pressures in the bottom row were found by multiplying the mole fraction of each gas by the total pressure:
\[P_i = \chi_i P_{tot} \nonumber\]
with the term in the denominator of each mole fraction is the total number of moles of gas present at equilibrium:
\[P_{tot} = (0.200 – x) + (3.00 + x) + x = 3.20 + x \nonumber\]
Substituting the equilibrium partial pressures into the equilibrium expression, we have
\[ \dfrac{ (3.00 +x)(x)}{(0.200 -x)(3.20 +x)} = 3.60 \nonumber\]
whose polynomial form is
\[4.60x^2 + 13.80x – 2.304 = 0. \nonumber\]
You can use the quadratic question to solve this or you can do it graphically (more useful for higher order equations). Plotting this on a graphical calculator yields \(x = 0.159\) as the positive root:
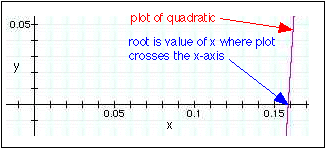
Substitution of this root into the expressions for the equilibrium partial pressures in the table yields the following values:
- \(P_{\ce{PCl5}}\) = 0.012 atm,
- \(P_{\ce{PCl3}}\) = 0.94 atm,
- \(P_{\ce{Cl2}}\) = 0.047 atm.
Effects of Dilution on Equilibrium
In the section that introduced the Le Chatelier principle, it was mentioned that diluting a weak acid such as acetic acid \(\ce{CH3COOH}\) (“\(\ce{HAc}\)”) will shift the dissociation equilibrium to the right:
\[\ce{HAc + H_2O \rightleftharpoons H_3O^{+} + Ac^{–}} \nonumber\]
Thus a \(0.10\,M\) solution of acetic acid is 1.3% ionized, while in a 0.01 M solution, 4.3% of the \(\ce{HAc}\) molecules will be dissociated. This is because as the solution becomes more dilute, the product [H3O+][Ac–] decreases more rapidly than does the \(\ce{[HAc]}\) term. At the same time the concentration of \(\ce{H2O}\) becomes greater, but because it is so large to start with (about 55.5 M), any effect this might have is negligible, which is why no \(\ce{[H2O]}\) term appears in the equilibrium expression.
For a reaction such as
\[\ce{CH_3COOH (l) + C_2H_5OH (l) \rightleftharpoons CH_3COOC_2H_5 (l) + H_2O (l) }\]
(in which the water concentration does change), dilution will have no effect on the equilibrium; the situation is analogous to the way the pressure dependence of a gas-phase reaction depends on the number of moles of gaseous components on either side of the equation (i.e., \(\Delta n_g\)).
The biochemical formation of a disaccharide (double) sugar from two monosaccharides is exemplified by the reaction
\[\text{fructose} (aq) + \text{glucose-6-phosphate} (aq) → \text{sucrose-6-phosphate} (aq) + \ce{H2O} (l)\]
(Sucrose is ordinary table sugar.) To what volume should a solution containing 0.050 mol of each monosaccharide be diluted in order to bring 5% conversion to sucrose phosphate? The equilibrium constant for this reaction is \(K_{c} = 7.1 \times 10^{-6}\) at room temperature.
Solution
The initial and final numbers of moles in this equation are as follows:
| ICE Table | fructose (\(\text{fruc}\)) | glucose-6-P (\(\text{gluc6P}\)) | sucrose-6-P (\(\text{suc6P}\)) | water \( \ce{H2O}\)) |
|---|---|---|---|---|
| Initial (moles) | 0.05 | 0.05 | 0 | - |
| Change (moles) | -x | -x | +x | - |
| Equilibrium (moles) | 0.05-x | 0.05-x | +x | - |
What is the value of \(x\)? That is when 5% of the reaction has proceeded or when 5% of the fructose (or glucose-6-P) is consumed:
\[\dfrac{x}{0.05} = 0.05 \nonumber\]
so \(x = 0.0025 \nonumber\). The equilibrated concentrations are then
- \([\text{suc6P}]_{equil} = \dfrac{0.0025}{V}\)
- \([\text{fruc}]_{equil} = \dfrac{0.0475}{V}\)
- \([\text{glu6P}]_{equil} = \dfrac{0.0475}{V}\)
Substituting into the values in for the expression of \(K_c\) (in which the solution volume is the unknown), we have
\[\begin{align*} K_{c} &= \dfrac{[\text{suc6P}]_{equil} }{[\text{fruc}]_{equil} [\text{gluc6P}]_{equil} } \\[4pt] &= \dfrac{\left(\dfrac{0.0025}{V}\right)}{\left(\dfrac{0.0475}{V}\right)^2} = 7.1 \times 10^{-6} \end{align*}\]
\[V = (7.1 \times 10^{-6}) \dfrac{(0.0475)^2}{0.0025} \nonumber\]
Solving for \(V\) gives a final solution volume of \(6.4 \times 10^{-4}\,L\) or \(640 \mu L\). Why so small? The reaction is not favored and to push it forward, large concentrations of reactants are needed (Le Chatelier principle in action).


