8.10.9C: Weak and Strong Electrolytes
- Page ID
- 20111
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The serious study of electrolytic solutions began in the latter part of the 19th century, mostly in Germany — and before the details of dissociation and ionization were well understood. These studies revealed that the equivalent conductivities of electrolytes all diminish with concentration (or more accurately, with the square root of the concentration), but they do so in several distinct ways that are distinguished by their behaviors at very small concentrations. This led to the classification of electrolytes as weak, intermediate, and strong.
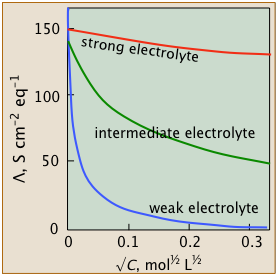
You will notice that plots of conductivities vs. √c start at c=0. It is of course impossible to measure the conductance of an electrolyte at vanishingly small concentrations (not to mention zero!), but for strong and intermediate electrolytes, one can extrapolate a series of observations to zero. The resulting values are known as limiting equivalent conductances or sometimes as "equivalent conductances at infinite dilution", designated by Λ°.
- Strong electrolytes
- These well-behaved systems include many simple salts such as NaCl, as well as all strong acids.
The Λ vs. √c plots closely follow the linear relation - Λ = Λ° – b √c
- Intermediate electrolytes
- These "not-so-strong" salts can't quite conform to the linear equation above, but their conductivities can be extrapolated to infinite dilution.
- Weak electrolytes
- "Less is more" for these oddities which possess the remarkable ability to exhibit infinite equivalent conductivity at infinite dilution. Although Λ° cannot be estimated by extrapolation, there is a clever work-around.
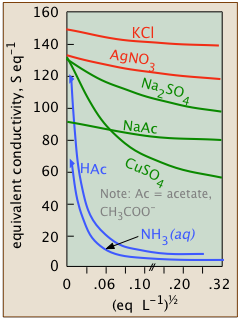
Conductivity diminishes as concentrations increase
Since ions are the charge carriers, we might expect the conductivity of a solution to be directly proportional to their concentrations in the solution. So if the electrolyte is totally dissociated, the conductivity should be directly proportional to the electrolyte concentration. But this ideal behavior is never observed; instead, the conductivity of electrolytes of all kinds diminishes as the concentration rises.
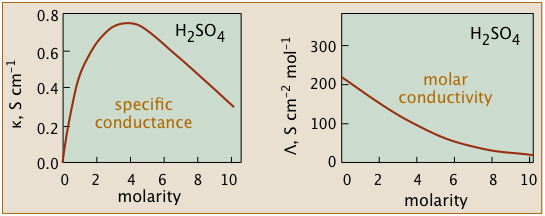
The non-ideality of electrolytic solutions is also reflected in their colligative properties, especially freezing-point depression and osmotic pressure. The primary cause of this is the presence of the ionic atmosphere that was introduced above. To the extent that ions having opposite charge signs are more likely to be closer together, we would expect their charges to partially cancel, reducing their tendency to migrate in response to an applied potential gradient.
A secondary effect arises from the fact that as an ion migrates through the solution, its counter-ion cloud does not keep up with it. Instead, new counter-ions are continually acquired on the leading edge of the motion, while existing ones are left behind on the opposite side. It takes some time for the lost counter-ions to dissipate, so there are always more counter-ions on the trailing edge. The resulting asymmetry of the counter-ion field exerts a retarding effect on the central ion, reducing its rate of migration, and thus its contribution to the conductivity of the solution.
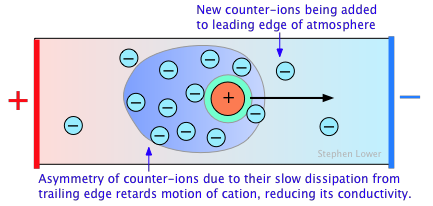
The quantitative treatment of these effects was first worked out by P. Debye and W. Huckel in the early 1920's, and was improved upon by Ostwald a few years later. This work represented one of the major advances in physical chemistry in the first half of the 20th Century, and put the behavior of electrolytic solutions on a sound theoretical basis. Even so, the Debye-Huckel theory breaks down for concentrations in excess of about 10–3 M L–1 for most ions.
Not all Electrolytes Totally Dissociate in Solution
plots for strong electrolytes is largely explained by the effects discussed immediately above. The existence of intermediate electrolytes served as the first indication that many salts are not completely ionized in water; this was soon confirmed by measurements of their colligative properties.
The curvature of the plots for intermediate electrolytes is a simple consequence of the Le Chatelier effect, which predicts that the equilibrium
\[MX_{(aq)} = M^+_{(aq)} + X^–_{(aq)}\]
will shift to the left as the concentration of the "free" ions increases. In more dilute solutions, the actual concentrations of these ions is smaller, but their fractional abundance in relation to the undissociated form is greater. As the solution approaches zero concentration, virtually all of the \(MX_{(aq)}\) becomes dissociated, and the conductivity reaches its limiting value.
Weak electrolytes are dissociated only at extremely high dilution
| hydrofluoric acid | HF | Ka = 10–3.2 |
| acetic acid | CH3COOH | Ka = 10–6.3 |
| bicarbonate ion | HCO3– | Ka = 10–10.3 |
| ammonia | NH3 | Kb = 10–4.7 |
Dissociation, of course, is a matter of degree. The equilibrium constants for the dissociation of an intermediate electrolyte salt MX are typically in the range of 1-200. This stands in contrast to the large number of weak acids (as well as weak bases) whose dissociation constants typically range from 10–3 to smaller than 10–10.
These weak electrolytes, like the intermediate ones, will be totally dissociated at the limit of zero concentration; if the scale of the weak-electrolyte plot (blue) shown above were magnified by many orders of magnitude, the curve would resemble that for the intermediate electrolyte above it, and a value for Λ° could be found by extrapolation. But at such a high dilution, the conductivity would be so minute that it would be masked by that of water itself (that is, by the H+ and OH– ions in equilibrium with the massive 55.6 M L–1 concentration of water) — making values of Λ in this region virtually unmeasurable.


