8.8: Ideal vs. Real Solutions
- Page ID
- 78439
Make sure you thoroughly understand the following essential ideas:
- Describe the physical reasons that a binary liquid solution might exhibit non-ideal behavior
The popular liquor vodka consists mainly of ethanol (ethyl alcohol) and water in roughly equal portions. Ethanol and water both have substantial vapor pressures, so both components contribute to the total pressure of the gas phase above the liquid in a closed container of the two liquids. One might expect the vapor pressure of a solution of ethanol and water to be directly proportional to the sums of the values predicted by Raoult's law for the two liquids individually, but in general, this does not happen. The reason for this can be understood if you recall that Raoult's law reflects a single effect: the smaller proportion of vaporizable molecules (and thus their reduced escaping tendency) when the liquid is diluted by otherwise "inert" (non-volatile) substance.
Ideal Solutions
There are some solutions whose components follow Raoult's law quite closely. An example of such a solution is one composed of hexane C6H14 and heptane C7H16. The total vapor pressure of this solution varies in a straight-line manner with the mole fraction composition of the mixture.
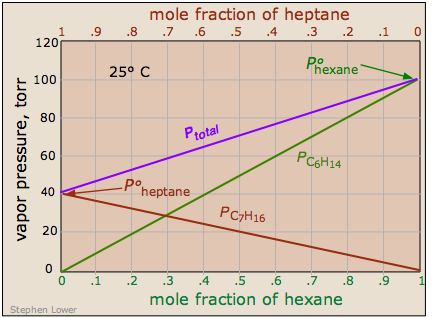
Note that the mole fraction scales at the top and bottom run in opposite directions, since by definition,
\[\chi_{hexane} = 1 – \chi_{heptane}\]
If this solution behaves ideally, then is the sum of the Raoult's law plots for the two pure compounds:
\[P_{total} = P_{ heptane } + P_{ hexane }\]
An ideal solution is one whose vapor pressure follows Raoult's law throughout its range of compositions. Experience has shown solutions that approximate ideal behavior are composed of molecules having very similar structures. Thus hexane and heptane are both linear hydrocarbons that differ only by a single –CH2 group. This provides a direct clue to the underlying cause of non-ideal behavior in solutions of volatile liquids. In an ideal solution, the interactions are there, but they are all energetically identical. Thus in an ideal solution of molecules A and B, A—A and B—B attractions are the same as A—B attractions. This is the case only when the two components are chemically and structurally very similar.
Ideal Solutions vs. Ideal Gases
The ideal solution differs in a fundamental way from the definition of an ideal gas, defined as a hypothetical substance that follows the ideal gas law. The kinetic molecular theory that explains ideal gas behavior assumes that the molecules occupy no space and that intermolecular attractions are totally absent.
The definition of an ideal gas is clearly inapplicable to liquids, whose volumes directly reflect the volumes of their component molecules. And of course, the very ability of the molecules to form a condensed phase is due to the attractive forces between the molecules. So the most we can say about an ideal solution is that the attractions between its all of its molecules are identical — that is, A-type molecules are as strongly attracted to other A molecules as to B-type molecules. Ideal solutions are perfectly democratic: there are no favorites.
Real Solutions
Real solutions are more like real societies, in which some members are "more equal than others." Suppose, for example, that unlike molecules are more strongly attracted to each other than are like molecules. This will cause A–B pairs that find themselves adjacent to each other to be energetically more stable than A–A and B–B pairs. At compositions in which significant numbers of both kind of molecules are present, their tendencies to escape the solution — and thus the vapor pressure of the solution, will fall below what it would be if the interactions between all the molecules were identical. This gives rise to a negative deviation from Raoult's law. The chloroform-acetone system, illustrated above, is a good example.

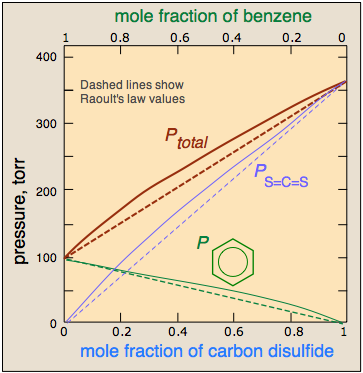
Conversely, if like molecules of each kind are more attracted to each other than to unlike ones, then the molecules that happen to be close to their own kind will be stabilized. At compositions approaching 50 mole-percent, A and B molecules near each other will more readily escape the solution, which will therefore exhibit a higher vapor pressure than would otherwise be the case. It should not be surprising molecules as different as benzene and \(CS_2\) should interact more strongly with their own kind, hence the positive deviation illustrated here.
You will recall that all gases approach ideal behavior as their pressures approach zero. In the same way, as the mole fraction of either component approaches unity, the behavior of the solution approaches ideality. This is a simple consequence of the fact that at these limits, each molecule is surrounded mainly by its own kind, and the few A-B interactions will have little effect. Raoult's law is therefore a limiting law:
\[P_i = \lim_{x_i \rightarrow 0} P^o \chi_i\]
it gives the partial pressure of a substance in equilibrium with the solution more and more closely as the mole fraction of that substance approaches unity.


