Water Physics

Physical Properties of Water

Chemical and physical properties of water are often discussed together. These properties are fundamentals of many disciplines such as hydrology, environmental studies, chemical engineering, environmental engineering, civil engineering etc. They are of interest to chemists and physicists of course.

Here are some highlights of the physical properties of water. Pure liquid water has a high heat capacity of 4.182 J K^-1 g^-1; it is a good heat conductor, but a poor electric conductor. It is a solvent for dissolving ionic and polar substances, but interact with non-polar substance weakly. Surface tension of water is rather high, and little quantities aggregate into drops rather than spread out as thin layers.

Hydrogen bonding contributes to many of the physical and chemical properties, such as the unusual but normally known freezing point of 273.15 K, and 373.15 K respectively. The critical temperature and pressure are 647.3 K and 220.5 bar (22050 kPa) and critical volume = 0.056 m³ kmol^-1.

Because of the many applications of water, some more details on the properties of water are desirable. Thus, keeping track of water properties is of national interest. For example, the American Society of Mechanical Engineers (ASME) is such an organization. International co-operation on research and information exchange are more economical, and for thermal properties, The International Association for the Properties of Water and Steam (IAPWS) is set up. Canada is a member of this organization.

From the application point of view, the variations of the following properties as functions of temperature and pressure are required.

• Compressibility of steam and water as a function of pressure at various temperature
• Density of water as a function of temperature
• Viscosity of water as a function of temperature
• Enthalpy of water for various thermodynamic evaluations
• Molar volumes and expansion coefficients of water and vapor as functions of pressure and temperature
• Speed of sound in water and vapor and speed of sound in air-vapor mixture as functions of temperature and pressure
• Entropy of water as a function of temperature and pressure
• Thermal conductivity of water and steam
• Viscosity of water at any temperature for pipe and pump design
• Dielectric constant as functions of temperature and pressure
• Surface tension as functions of temperature and pressure
• Gibbs energy at various temperature and pressure
• Properties such as dielectric constants and ion products of supercritical water (fluid)
• Applications of supercritical water: Plastic waste recycle, recovery of toluenediamine, hydrolysis of PET (polyethylene terephthalate) etc.

We will discuss some of these to illustrate the point, but not all of them.

Density of Water

Density of Water
T /K	Density g/mL	D2O
273	0.999841	1.10469
274	0.999900
275	0.999941
276	0.999965
277	0.999973	1.1057
278	0.999965	1.10562
279	0.999941
280	0.999902
281	0.999849
282	0.999781
281	0.999700

Density is the mass per unit volume. The density of water is usually taken as 1.0 g/mL or 1.000e3 kg m^-3 at 277 K. This suggests that the density varies with temperature and water density is the highest at 277 K, and the density between 273 and 281 K from the CRC Handbook of Chemistry and Physics are given in the Table here. These data are calculated from experimental data for pure water based on the standard at 276.98 K. The same source gives the density of ordinary water as 1.000000 g/mL at 277 K.

The volume occupied by one mole of substance is called the molar volume. The molar volume of liquid water is 18.016/density. At 277 K, the molar volume is 18.016 mL. For liquid water, the molar volumes of liquid water increase to 18.03 mL at both 269 K and 285 K.

The density of ice is 0.917 at 273 K, and the molar volume is 19.65 mL, 9% more than the molar of liquid. Thus, 9% of an ice cube containing no air bubble float above the surface, and 91% of it is below the waterline. The density makes behavior of icebergs interesting. Ice bergs are major tourist attractions in Newfoundland and Labrador, Canada.

Electric Dipole Moment and Dielectric Constant

Charged ions interact with each other due to electrostatic attraction or repulsion. The force F between two charge particles with charges q₁, and q₂ separated by a distance r is

q1 q2
F = ------------
4 p eo r2

Cl d- | Na d+

Uncharged molecules still interact with each other, not due to electrostatic interaction, but due to electric dipole interaction. The electric dipole moment is a vector due to uneven distribution of unlike charges. In diatomic systems, the magnitude of the electric dipole moment can be estimated as the difference between the Pauling electronegativities of the two atoms. For convenience, let us assume that centres of positive and negatives of Na-Cl are separated by a distance l, then the electric dipole moment, \(\mu\) is

m = q l

Traditionally, the dipole moments of molecules have been tabulated in electrostatic units, in which case the charge of an electron is 4.80e-10 esu (= (1.6e-19 C) (3e9 esu/C)). In NaCl crystals, the distance between Na and Cl ions is 240 pm. If the NaCl molecule (in a gas) has the same distance between the ideallized ions, then the dipole moment is calculated below:

m = q l
= (1.60e-19) (240e-12 m)
= 3.84e-29 C m.

or in cgs-esu units
m = 4.8e-10 esu * 2.40e-8 cm
= 11.5e-18 esu cm

In the cgs-esu unit, 1e-18 esu cm is define a Debye (symbol D). Thus, we have

1 D = 1e-18 esu cm
= 3.355e-30 C m (from the calculation above)
m = 11.5 D for ideallized NaCl gas molecule
but
mobserved = 9 D in NaCl gas =3e-29 C m.

Electric Dipole Moment of Some Gas Molecules
Molecule	m /D
NaCl	9.0
KCl	10.3
CO	0.1
HF	1.8
HCl	1.1
HBr	0.8
H2O	1.8
SO2	1.6
N2O	0.2
NH3	1.5

However, experimental dipole moment = 9 D for NaCl gas. Thus, the model for the calculation has to be modified to account for the partial delocalization of the charges or by including some covalent character in the Na-Cl bond. In any case, the model shows a physical method (model) for the evaluation of dipole moment. Dipole moments of some gas molecules are given in the table here.

The dipole moment is a vector from the negative to the positive charge along the bond. For triatomic moecules such as those of water, the total electric dipole moment is the sum of al dipoles for each bond. The experimental dipole moment for water is 1.8 D, which is the same as that of H-F. Water is a very polar compound. Ammonia with three N-H bonds has a dipole moment of 1.5 D.

Homonuclear diatomic molecules have zero dipole moment, of course. So are linear CO₂ and CS₂ molecules.

The high dipole moment makes water a very special substance. Water has a very high dielectric constant, 80. Due to dipole-charge interaction, water is the universal solvent for ionic substances, especially mono-valent ions. The diagram below shows some typical ion-dipole and dipole-dipole interaction in solutions. The dissolution in water is called hydration.

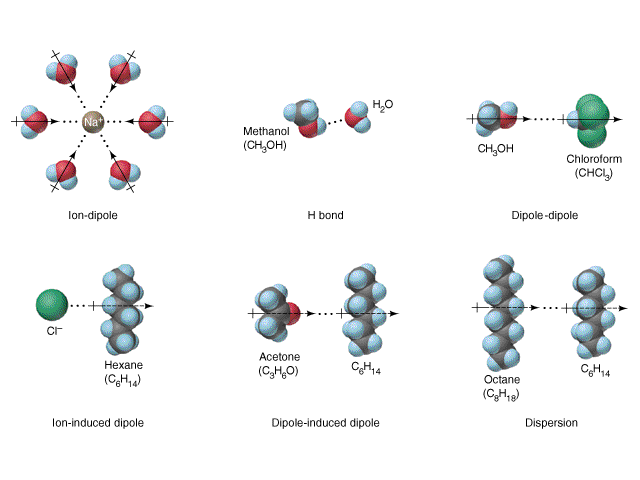
The dipole moment has something to do with its interaction with microwave. Application of Ground Penetrating Radar in Glaciology is a web site that gives the theory of radar and discusses the interaction of radar with water. It further illustrates the application in glaciology.

In contrast, supercritical water has a low dielectric constant, making it a good solvent for non-polar substances.

Example 1

Let us assume the H-F molecule as composed of two ions, a positive and a negative ion. What is the distance that separating these two ions in order to give a dipole moment of 1.8 D?

Solution
Recall the first formula from the discussion of dipole moment above, and proceed with the calculation as shown:

m = q l

q l = 4.8e-10 esu * l
= 1.8e-18 esu cm.

1.8e-18 esu cm
l = ----------------- = 0.375e-8 cm (37.5 pm)
4.8e-10 esu

DISCUSSION
What is the normal H-F bond distance? (Ans. 92 pm).

Dividing the apparent bondlength of 38 pm by the observed bondlength 92 pm gives the ionic character 38/92 = 41 % ionic character.

Questions

1. In a fire or nuclear power generator, steam at 600ºC under pressure is often used to transfer the heat from the boiler to the turbine. What phase is this steam?

Solutions

1. Hint: supercritical fluid of water.

Contributors and Attributions

• Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)