5.3: Hydrophobic Collapse

Hydrophobic Collapse¹

We see that hydrophobic particles in water will attempt to minimize their surface area with water by aggregating or phase separating. This process, known as hydrophobic collapse, is considered to be the dominant effect driving the folding of globular proteins.

Let’s calculate the free energy change for two oil droplets coalescing into one. The smaller droplets both have a radius R₀ and the final droplet a radius of \(R\).

\[\Delta G_{\text{collapse}} = \Delta G_{\text{sol}} (R) - 2 \Delta G_{\text{sol}} (R_0) \nonumber\]

The total volume of oil is constant—only the surface area changes. If the total initial surface area is \(A_0\), and the final total surface area is \(A\), then

\[\Delta G_{\text{collapse}} = (A - A_0) \gamma \nonumber\]

which is always negative since \(A < A_0\) and \(\gamma\) is positive.

This neglects the change in translational entropy due to two drops coalescing into one. Considering only the translational degrees of freedom of the drops, this should be approximately \(\Delta S_{\text{collapse}} \approx k_B \ln (3/6)\). In other words, a small number compared to the surface term.

We can readily generalize this to a chain of \(n\) beads, each of radius \(R_0\), which collapse toward a single sphere with the same total volume. In this case, let’s consider how the free energy of the system varies with the number of beads that have coalesced.

Again the total volume is constant, \(V=n\left(\dfrac{4}{3} \pi R_{0}^{3}\right)\) and the surface area changes. The initial surface area is \(A_{0}=m 4 \pi R_{0}^{2}\) and the final surface area is \(A_{\min }=4 \pi \left (R_{\min } \right)^{2} = m^{2/3} 4 \pi R_{0}^{2}\). Along the path, there is a drop of total surface area for each bead that coalesces. Let’s consider one path, in which an individual bead coalesces with one growing drop. The total surface area once \(n\) of \(m\) particles have coalesced is

\(A_n\) = (surface area of drop formed by \(n\) coalesced beads) + (total area of remaining \(m-n\) beads)

\[\begin{array} {rcl} {A_n} & = & {(n^{2/3} 4\pi R_0^2) + (m - n) 4\pi R_0^2} \\ {} & = & {(m + n^{2/3} - n)4\pi R_0^2} \\ {} & = & {A_0 + (n^{2/3} - n)4\pi R_0^2} \end{array}\nonumber\]

The free energy change for coalescing \(n\) beads is

\[\begin{array} {rcl} {\Delta G_{\text{coll}}} & = & {(A_n - A_0) \gamma } \\ {} & = & {(n^{2/3} - n) 4\pi R_0^2 \gamma} \end{array} \nonumber\]

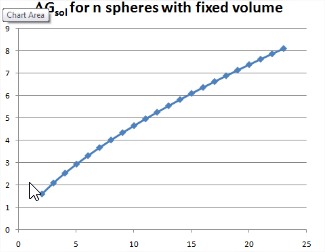
This free energy is plotted as a function of the bead number at fixed volume. This is an energy landscape that illustrates that the downhill direction of spontaneous change leads to a smaller number of beads. The driving force for the collapse of this chain can be considered to be the decrease in free energy as a function of the number of beads in the chain:

\[\begin{array} {c} {f_{\text{coll}} = -\dfrac{\partial \Delta G_{\text{coll}}}{\partial r} \propto - \dfrac{\partial \Delta G_{\text{coll}}}{\partial n}} \\ {-\dfrac{\partial \Delta G_{\text{coll}}}{\partial n} = 4\pi R_0^2 \gamma \left (1 - \dfrac{2}{3} n^{-1/3} \right )} \end{array} \nonumber\]

This is not a real force expressed in Newtons, but we can think of it as a pseudo-force, with the bead number acting as a proxy for the chain extension. If you want to extend a hydrophobic chain, you must do work against this. Written in terms of the extension of the chain \(x\) (not the drop area \(A\))

\[w=-\int_{x_{0}}^{x} f_{ext} d x = \int_{x_{0}}^{x} \left (\dfrac{\partial \Delta G_{coll}}{\partial A_{n}}\right) \left(\dfrac{\partial A_{n}}{\partial x}\right) d x\nonumber\]

Here we still have to figure out the relationship between extension and surface area, \(\partial A_{n} / \partial x\).

Alternatively, we can think of the collapse coordinate as the number of coalesced beads, \(n\).

Hydrophobic Collapse and Shape Fluctuations

An alternate approach to thinking about this problem is in terms of the collapse of a prolate ellipsoid to a sphere as is seeks to minimize its surface area. We take the ellipsoid to have a longradius \(\ell /2\) and a short radius \(r\). The area and volume are then:

\[
\begin{array}{l}
A=2 \pi\left(r^{2}+\frac{\ell^{2}}{4} \frac{\alpha}{\tan \alpha}\right) \quad \alpha=\cos ^{-1}\left(\frac{2 r}{\ell}\right) \\
V=\frac{2}{3} \pi r^{2} \ell \quad(\text { constant }) \\
\therefore \quad r^{2}=3 V / 2 \pi \ell \\
A=\left(\frac{3 V}{\ell}+\pi \frac{\ell^{2}}{2} \frac{\alpha}{\tan \alpha}\right)
\end{array}
\nonumber\]

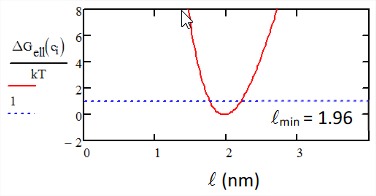
Let’s plot the free energy of this ellipsoid as a function of \(\ell\). For \(V = 4\ nm^3\), \(k_B T = 4.1\ pN/nm\) we find \(\ell_{\min} = 1.96\ nm\). Note that at \(k_B T\) the dimensions of the ellipsoid can fluctuate over many \(\sim 5 \mathring{A}\).

Readings

1. N. T. Southall, K. A. Dill and A. D. J. Haymet, A view of the hydrophobic effect, J. Phys. Chem. B 106, 521–533 (2002).
2. D. Chandler, Interfaces and the driving force of hydrophobic assembly, Nature 437, 640–647 (2005).
3. G. Hummer, S. Garde, A. E. García, M. E. Paulaitis and L. R. Pratt, Hydrophobic effects on a molecular scale, J. Phys. Chem. B 102, 10469–10482 (1998).
4. B. J. Berne, J. D. Weeks and R. Zhou, Dewetting and hydrophobic interaction in physical and biological systems, Annu. Rev. Phys. Chem. 60, 85–103 (2009).

____________________________________________

1. See K. Dill and S. Bromberg, Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience. (Taylor & Francis Group, New York, 2010), p. 675.