Writing Equations for Redox Reactions
- Page ID
- 3659
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page explains how to work out electron-half-reactions for oxidation and reduction processes, and then how to combine them to give the overall ionic equation for a redox reaction. This is an important skill in inorganic chemistry.
Electron-half-equations
The ionic equation for the magnesium-aided reduction of hot copper(II) oxide to elemental copper is given below :
\[\ce{Cu^{2+} + Mg \rightarrow Cu + Mg^{2+}}\nonumber \]
The equation can be split into two parts and considered from the separate perspectives of the elemental magnesium and of the copper(II) ions. This arrangement clearly indicates that the magnesium has lost two electrons, and the copper(II) ion has gained them.
\[ \ce{ Mg \rightarrow Mg^{2+} + 2e^-}\nonumber \]
\[\ce{Cu^{2+} + 2e^-} \rightarrow Cu\nonumber \]
These two equations are described as "electron-half-equations," "half-equations," or "ionic-half-equations," or "half-reactions." Every redox reaction is made up of two half-reactions: in one, electrons are lost (an oxidation process); in the other, those electrons are gained (a reduction process).
Working out electron-half-equations and using them to build ionic equations
In the example above, the electron-half-equations were obtained by extracting them from the overall ionic equation. In practice, the reverse process is often more useful: starting with the electron-half-equations and using them to build the overall ionic equation.
Chlorine gas oxidizes iron(II) ions to iron(III) ions. In the process, the chlorine is reduced to chloride ions. From this information, the overall reaction can be obtained. The chlorine reaction, in which chlorine gas is reduced to chloride ions, is considered first:
\[\ce{ Cl_2 \rightarrow Cl^{-}}\nonumber \]
The atoms in the equation must be balanced:
\[\ce{ Cl_2 \rightarrow 2Cl^{-}}\nonumber \]
This step is crucial. If any atoms are unbalanced, problems will arise later.
To completely balance a half-equation, all charges and extra atoms must be equal on the reactant and product sides. In order to accomplish this, the following can be added to the equation:
- electrons
- water
- hydrogen ions (unless the reaction is being done under alkaline conditions, in which case, hydroxide ions must be added and balanced with water)
In the chlorine case, the only problem is a charge imbalance. The left-hand side of the equation has no charge, but the right-hand side carries 2 negative charges. This is easily resolved by adding two electrons to the left-hand side. The fully balanced half-reaction is:
\[\ce{ Cl_2 +2 e^- \rightarrow 2Cl^{-}}\nonumber \]
Next the iron half-reaction is considered. Iron(II) ions are oxidized to iron(III) ions as shown:
\[ \ce{Fe^{2+} \rightarrow Fe^{3+}}\nonumber \]
The atoms balance, but the charges do not. There are 3 positive charges on the right-hand side, but only 2 on the left. To reduce the number of positive charges on the right-hand side, an electron is added to that side:
\[ \ce{Fe^{2+} \rightarrow Fe^{3+} } + e-\nonumber \]
The next step is combining the two balanced half-equations to form the overall equation. The two half-equations are shown below:
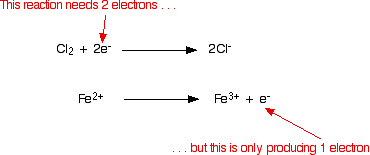
It is obvious that the iron reaction will have to happen twice for every chlorine reaction. This is accounted for in the following way: each equation is multiplied by the value that will give equal numbers of electrons, and the two resulting equations are added together such that the electrons cancel out:
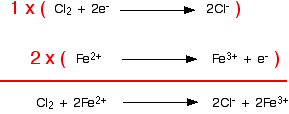
At this point, it is important to check once more for atom and charge balance. In this case, no further work is required.
The first example concerned a very simple and familiar chemical equation, but the technique works just as well for more complicated (and perhaps unfamiliar) chemistry.
Manganate(VII) ions, MnO4-, oxidize hydrogen peroxide, H2O2, to oxygen gas. The reaction is carried out with potassium manganate(VII) solution and hydrogen peroxide solution acidified with dilute sulfuric acid. As the oxidizing agent, M anganate (VII) is reduced to manganese(II).
The hydrogen peroxide reaction is written first according to the information given:
\[ \ce{H_2O_2 \rightarrow O_2} \nonumber \]
The oxygen is already balanced, but the right-hand side has no hydrogen.
All you are allowed to add to this equation are water, hydrogen ions and electrons. Adding water is obviously unhelpful: if water is added to the right-hand side to supply extra hydrogen atoms, an additional oxygen atom is needed on the left. Hydrogen ions are a better choice.
Adding two hydrogen ions to the right-hand side gives:
\[ \ce{ H_2O_2 \rightarrow O_2 + 2H^{+}} \nonumber \]
Next the charges are balanced by adding two electrons to the right, making the overall charge on both sides zero:
\[ \ce{ H_2O_2 \rightarrow O_2 + 2H^{+} + 2e^{-}}\nonumber \]
Next the manganate(VII) half-equation is considered:
\[MnO_4^- \rightarrow Mn^{2+}\nonumber \]
The manganese atoms are balanced, but the right needs four extra oxygen atoms. These can only come from water, so four water molecules are added to the right:
\[ MnO_4^- \rightarrow Mn^{2+} + 4H_2O\nonumber \]
The water introduces eight hydrogen atoms on the right. To balance these, eight hydrogen ions are added to the left:
\[ MnO_4^- + 8H^+ \rightarrow Mn^{2+} + 4H_2O\nonumber \]
Now that all the atoms are balanced, only the charges are left. There is a net +7 charge on the left-hand side (1- and 8+), but only a charge of +2 on the right. 5 electrons are added to the left-hand side to reduce the +7 to +2:
\[ MnO_4^- + 8H^+ + 5e^- \rightarrow Mn^{2+} _ 4H_2O\nonumber \]
This illustrates the strategy for balancing half-equations, summarized as followed:
- Balance the atoms apart from oxygen and hydrogen.
- Balance the oxygens by adding water molecules.
- Balance the hydrogens by adding hydrogen ions.
- Balance the charges by adding electrons.
Now the half-equations are combined to make the ionic equation for the reaction.
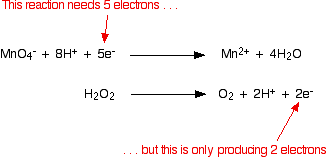
As before, the equations are multiplied such that both have the same number of electrons. In this case, the least common multiple of electrons is ten:
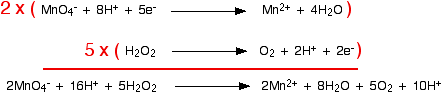
The equation is not fully balanced at this point. There are hydrogen ions on both sides which need to be simplified:

This often occurs with hydrogen ions and water molecules in more complicated redox reactions. Subtracting 10 hydrogen ions from both sides leaves the simplified ionic equation.
\[ 2MnO_4^- + 6H^+ + 5H_2O_2 \rightarrow 2Mn^{2+} + 8H_2O + 5O_2\nonumber \]
This technique can be used just as well in examples involving organic chemicals. Potassium dichromate(VI) solution acidified with dilute sulfuric acid is used to oxidize ethanol, CH3CH2OH, to ethanoic acid, CH3COOH.
The oxidizing agent is the dichromate(VI) ion, Cr2O72-, which is reduced to chromium(III) ions, Cr3+. The ethanol to ethanoic acid half-equation is considered first:
\[ CH_3CH_2OH \rightarrow CH_3COOH\nonumber \]
The oxygen atoms are balanced by adding a water molecule to the left-hand side:
\[ CH_3CH_2OH + H_2O \rightarrow CH_3COOH\nonumber \]
Four hydrogen ions to the right-hand side to balance the hydrogen atoms:
\[ CH_3CH_2OH + H_2O \rightarrow CH_3COOH + 4H^+\nonumber \]
The charges are balanced by adding 4 electrons to the right-hand side to give an overall zero charge on each side:
\[ CH_3CH_2OH + H_2O \rightarrow CH_3COOH + 4H^+ + 4e^-\nonumber \]
The unbalanced dichromate (VI) half reaction is written as given:
\[ Cr_2O_7^{2-} \rightarrow Cr^{3+}\nonumber \]
At this stage, students often forget to balance the chromium atoms, making it impossible to obtain the overall equation. To avoid this, the chromium ion on the right is multiplied by two:
\[ Cr_2O_7^{2-} \rightarrow 2Cr^{3+}\nonumber \]
The oxygen atoms are balanced by adding seven water molecules to the right:
\[ Cr_2O_7^{2-} \rightarrow 2Cr^{3+} + 7H_2O\nonumber \]
The resulting hydrogen atoms are balanced by adding fourteen hydrogen ions to the left:
\[ Cr_2O_7^{2-} + 14H^+ \rightarrow 2Cr^{3+} + 7H_2O\nonumber \]
Six electrons are added to the left to give a net +6 charge on each side.
\[ Cr_2O_7^{2-} + 14H^+ + 6e^- \rightarrow 2Cr^{3+} + 7H_2O\nonumber \]
The two balanced half reactions are summarized:
\[ CH_3CH_2OH + H_2O \rightarrow CH_3COOH + 4H^+ + 4e^-\nonumber \]
\[ Cr_2O_7^{2-} + 14H^+ + 6e^- \rightarrow 2Cr^{3+} + 7H_2O\nonumber \]
The least common multiple of 4 and 6 is 12. Therefore, the first equation is multiplied by 3 and the second by 2, giving 12 electrons in each equation:
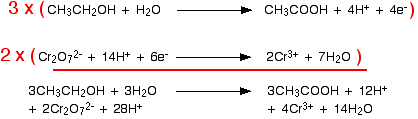
Simplifying the water molecules and hydrogen ions gives final equation:
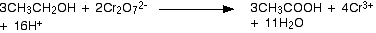
Balancing reactions under alkaline conditions
Working out half-equations for reactions in alkaline solution is decidedly more tricky than the examples above. As some curricula do not include this type of problem, the process for balancing alkaline redox reactions is covered on a separate page.


