7.4: Low Energy Electron Diffraction
- Page ID
- 55907
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Low energy electron diffraction (LEED) is a very powerful technique that allows for the characterization of the surface of materials. Its high surface sensitivity is due to the use of electrons with energies between 20-200 eV, which have wavelengths equal to 2.7 – 0.87 Å (comparable to the atomic spacing). Therefore, the electrons can be elastically scattered easily by the atoms in the first few layers of the sample. Its features, such as little penetration of low–energy electrons have positioned it as one of the most common techniques in surface science for the determination of the symmetry of the unit cell (qualitative analysis) and the position of the atoms in the crystal surface (quantitative analysis).
History: Davisson and Germer Experiment
In 1924 Louis de Brogile postulated that all forms of matter, such as electrons, have a wave-particle nature. Three years later after this postulate, the American physicists Clinton J. Davisson and Lester H. Germer (Figure \(\PageIndex{1}\)) proved experimentally the wave nature of electrons at Bell Labs in New York, see Figure 1. At that time, they were investigating the distribution-in-angle of the elastically scattered electrons (electrons that have suffered no loss of kinetic energy) from the (111) face of a polycrystalline nickel, material composed of many randomly oriented crystals.

The experiment consisted of a beam of electrons from a heated tungsten filament directed against the polycrystalline nickel and an electron detector, which was mounted on an arc to observe the electrons at different angles. During the experiment, air entered in the vacuum chamber where the nickel was, producing an oxide layer on its surface. Davisson and Clinton reduced the nickel by heating it at high temperature. They did not realize that the thermal treatment changed the polycrystalline nickel to a nearly monocrystalline nickel, material composed of many oriented crystals. When they repeated the experiment, it was a great surprise that the distribution-in-angle of the scattered electrons manifested sharp peaks at certain angles. They soon realized that these peaks were interference patterns, and, in analogy to X-ray diffraction, the arrangement of atoms and not the structure of the atoms was responsible for the pattern of the scattered electrons.
The results of Davisson and Germer were soon corroborated by George Paget Thomson, J. J. Thomson’s son. In 1937, both Davisson and Thomson were awarded with the Nobel Prize in Physics for their experimental discovery of the electron diffraction by crystals. It is noteworthy that 31 years after J. J. Thomson showed that the electron is a particle, his son showed that it is also a wave.
Although the discovery of low-energy electron diffraction was in 1927, it became popular in the early 1960’s, when the advances in electronics and ultra-high vacuum technology made possible the commercial availability of LEED instruments. At the beginning, this technique was only used for qualitative characterization of surface ordering. Years later, the impact of computational technologies allowed the use of LEED for quantitative analysis of the position of atoms within a surface. This information is hidden in the energetic dependence of the diffraction spot intensities, which can be used to construct a LEED I-V curve.
Principles and Diffraction Patterns
Electrons can be considered as a stream of waves that hit a surface and are diffracted by regions with high electron density (the atoms). The electrons in the range of 20 to 200 eV can penetrate the sample for about 10 Å without loosing energy. Because of this reason, LEED is especially sensitive to surfaces, unlike X-ray diffraction, which gives information about the bulk-structure of a crystal due to its larger mean free path (around micrometers). Table \(\PageIndex{1}\) compares general aspects of both techniques.
| Low Energy Electron Diffraction | X-ray Diffraction |
| Surface structure determination (high surface sensitivity) | Bulk structures determination |
| Sample single crystal | Sample single-crystal or polycrystalline |
| Sample must be have an oriented surface, sensitive to impurities | Surface impurities not important |
| Experiment in ultra-high vacuum | Experiment usually at atmospheric pressure |
| Experiment done mostly at constant incidence angle and variable wavelength (electron energy) | Constant wavelength and variable incidence angle |
| Diffraction pattern consists of beams visible at almost all energies | Diffraction pattern consists of beams flashing out at specific wavelengths and angles |
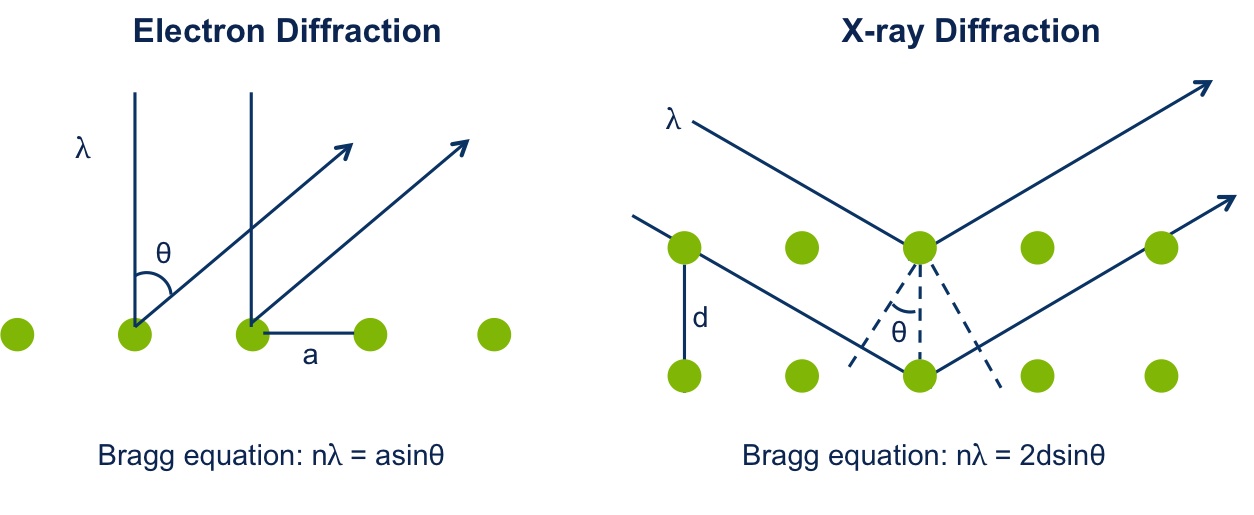
Like X-ray diffraction, electron diffraction also follows the Bragg’s law, see Figure \(\PageIndex{2}\), where λ is the wavelength, a is the atomic spacing, d is the spacing of the crystal layers, θ is the angle between the incident beam and the reflected beam, and n is an integer. For constructive interference between two waves, the path length difference (2a sinθ / 2d sinθ) must be an integral multiple of the wavelength.
In LEED, the diffracted beams impact on a fluorescent screen and form a pattern of light spots (Figure \(\PageIndex{3}\) a), which is a to-scale version of the reciprocal lattice of the unit cell. The reciprocal lattice is a set of imaginary points, where the direction of a vector from one point to another point is equal to the direction of a normal to one plane of atoms in the unit cell (real space). For example, an electron beam penetrates a few 2D-atomic layers, Figure \(\PageIndex{3}\) b), so the reciprocal lattice seen by LEED consists of continues rods and discrete points per atomic layer, see Figure \(\PageIndex{3}\) c. In this way, LEED patterns can give information about the size and shape of the real space unit cell, but nothing about the positions of the atoms. To gain this information about atomic positions, analysis of the spot intensities is required. For further information about reciprocal lattice and crystals refer to Crystal Structure and An Introduction to Single-Crystal X-Ray Crystallography.
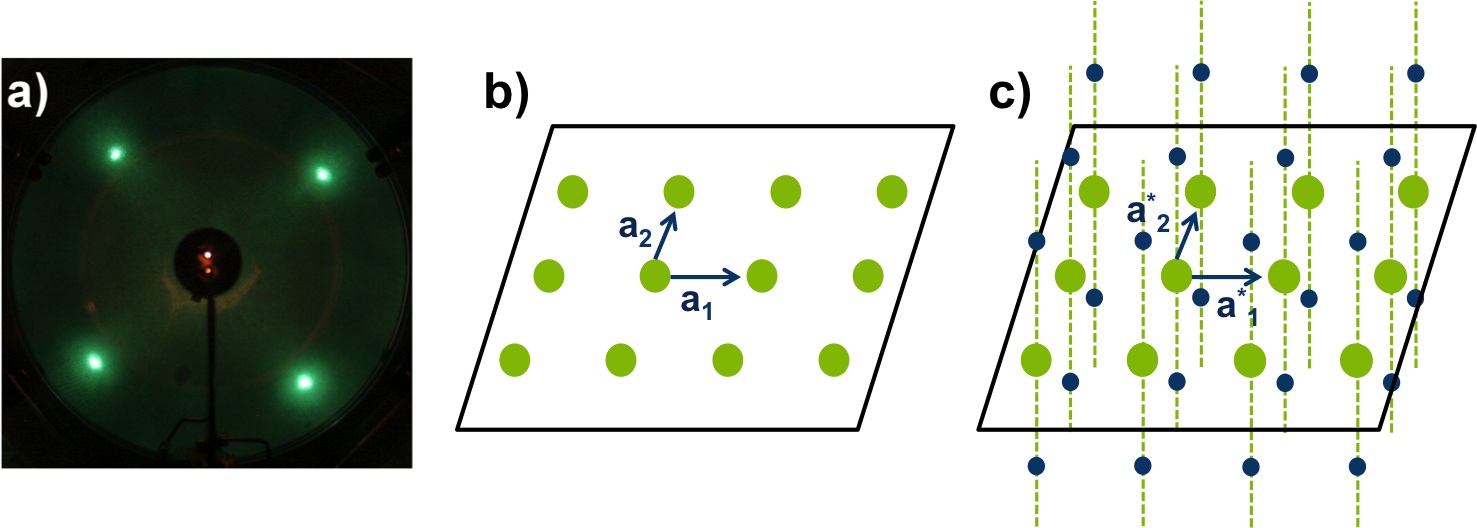
Thanks to the hemispheric geometry of the green screen of LEED, we can observe the reciprocal lattice without distortion. It is important to take into account that the separation of the points in the reciprocal lattice and the real interplanar distance are inversely proportional, which means that if the atoms are more widely spaced, the spots in the pattern get closer and vice versa. In the case of superlattices, a periodic structure composed of layers of two materials, new points arise in addition to the original diffraction pattern.
LEED Experimental Equipment
The typical diagram of a LEED system is shown in Figure \(\PageIndex{4}\). This system sends an electron beam to the surface of the sample, which comes from an electron gun behind a transparent hemispherical fluorescent screen. The electron gun consists of a heated cathode and a set of focusing lenses which send electrons at low energies. The electrons collide with the sample and diffract in different directions depending on the surface. Once diffracted, they are directed to the fluorescent screen. Before colliding with the screen, they must pass through four different grids (known as retarding grids), which contain a central hole through which the electron gun is inserted. The first grid is the nearest one to the sample and is connected to earth ground. A negative potential is applied to the second and third grids, which act as suppressor grids, given that they repel all electrons coming from non–elastic diffractions. These grids perform as filters, which only allow the highest–energy electrons to pass through; the electrons with the lowest energies are blocked in order to prevent a bad resolution image. The fourth grid protects the phosphor screen, which possesses positive charge from the negative grids. The remaining electrons collide with the luminescent screen, creating a phosphor glow (left side of Figure \(\PageIndex{4}\)), where the light intensity depends on the electron intensity.
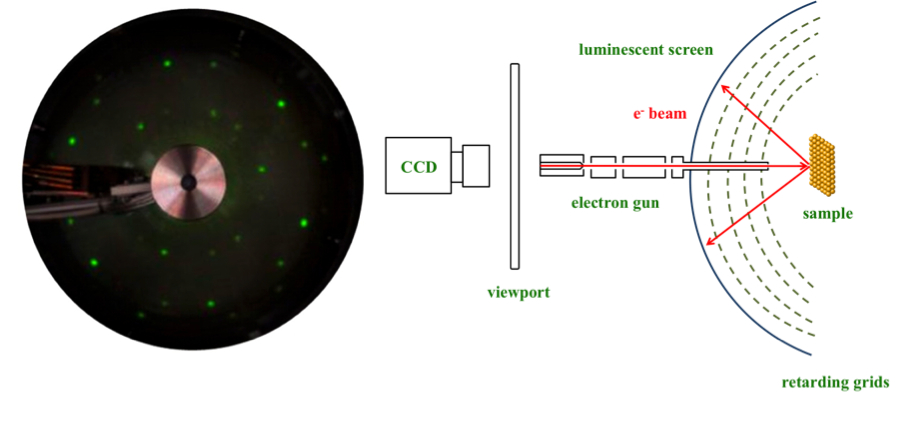
For conventional systems of LEED, it is necessary a method of data acquisition. In the past, the general method for analyzing the diffraction pattern was to manually take several dozen pictures. After the development of computers, the photographs were scanned and digitalized for further analysis through computational software. Years later, the use of the charge–coupled device (CCD) camera was incorporated, allowing rapid acquisition, the possibility to average frames during the acquisition in order to improve the signal, the immediate digitalization and channeling of LEED pattern. In the case of the IV curves, the intensities of the points are extracted making use of special algorithms. Figure \(\PageIndex{5}\) shows a commercial LEED spectrometer with the CCD camera, which has to be in an ultra-high vacuum vessel.

LEED Applications
We have previously talked about the discovery of LEED and its principles, along with the experimental setup of a LEED system. It was also mentioned that LEED provides qualitative and quantitative surface analysis. In the following section, we will discuss the most common applications of LEED and the information that one can obtain with this technique.
Study of Adsorbates on the Surface and Disorder Layers
ne of the principal applications of LEED is the study of adsorbates on catalysts, due to its high surface sensitivity. In order to illustrate the application of LEED in the study of adsorbates. As an example, Figure \(\PageIndex{6}\) a shows the surface of Cu (100) single crystal, the pristine material. This surface was cleaned carefully by various cycles of sputtering with ions of argon, followed by annealing. The LEED patter of Cu (100) presents four well-defined spots corresponding to its cubic unit cell.
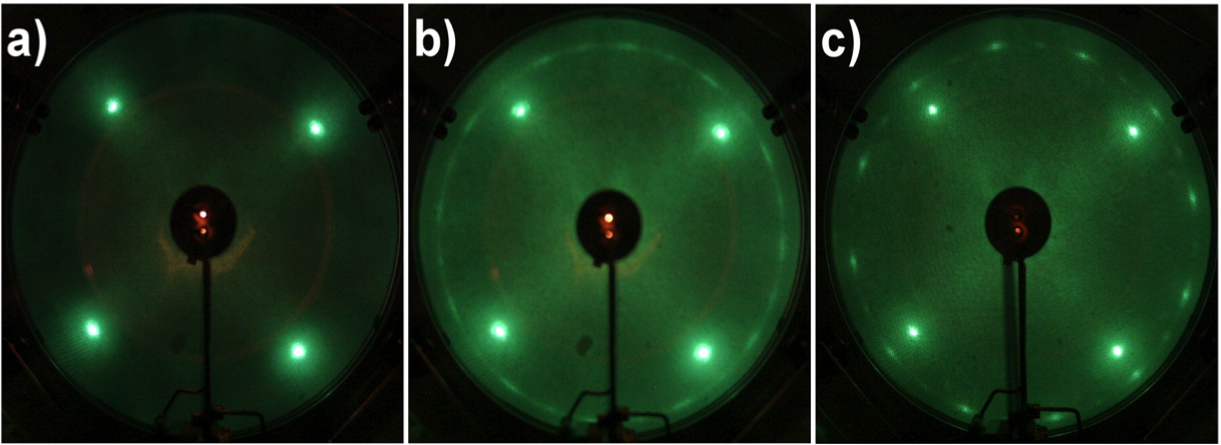
Figure \(\PageIndex{6}\) b shows the LEED pattern after the growth of graphene on the surface of Cu (100) at 800 °C, we can observe the four spots that correspond to the surface of Cu (100) and a ring just outside these spots, which correspond to the domains of graphene with four different primary rotational alignments with respect to the Cu (100) substrate lattice, see Figure \(\PageIndex{7}\). When increasing the temperature of growth of graphene to 900 °C, we can observe a ring of twelve spots (as seen in Figure \(\PageIndex{6}\) c), which indicates that the graphene has a much higher degree of rotational order. Only two domains are observed with an alignment of one of the lattice vectors to one of the Cu (100) surface lattice vectors, given that graphene has a hexagonal geometry, so that only one vector can coincide with the cubic lattice of Cu (100).
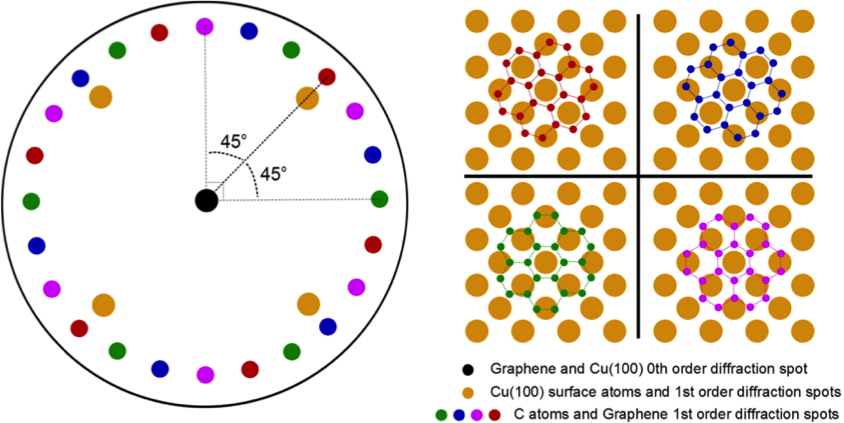
One possible explanation for the twelve spots observed at 900 ˚C is that when the temperature of all domains is increased the four different domains observed at 800 ˚C, may possess enough energy to adopt the two orientations in which the vectors align with the surface lattice vector of Cu (100). In addition, at 900 ˚C, a decrease in the size and intensity of the Cu (100) spots is observed, indicating a larger coverage of the copper surface by the domains of graphene.
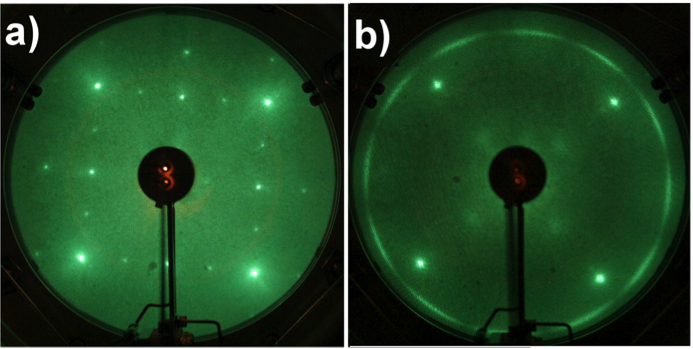
When the oxygen is chemisorbed on the surface of Cu (100), the new spots correspond to oxygen, Figure \(\PageIndex{8}\) a. Once graphene is allowed to grow on the surface with oxygen at 900 ˚C, the LEED pattern turns out different: the twelve spots corresponding to graphene domains are not observed due to nucleation of graphene domains in the presence of oxygen in multiple orientations, Figure \(\PageIndex{8}\) b.
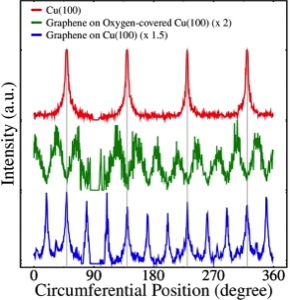
A way to study the disorder of the adsorbed layers is through the LEED–IV curves, see Figure \(\PageIndex{9}\). In this case, the intensities are in relation to the angle of the electron beam. The spectrum of Cu (100) with only four sharp peaks shows a very organized surface. In the case of the graphene sample growth over the copper surface, twelve peaks are shown, which correspond to the main twelve spots of the LEED pattern. These peaks are sharp, which indicate an high level of order. For the case of the sample of graphene growth over copper with oxygen, the twelve peaks widen, which is an effect of the increase of disorder in the layers.
Structure Determination
As previously mentioned, LEED–IV curves may give us exact information about the position of the atoms in a crystal. These curves are related to a variation of intensities of the diffracted electron (spots) with the energy of the electron beam. The process of determination of the structure by this technique works as ‘proof and error’ and consists of three main parts: the measurement of the intensity spectra, the calculations for various models of atomic positions and the search for the best-fit structure which is determined by an R-factor.
The first step consists of obtaining the experimental LEED pattern and all the electron beam intensities for every spot of the reciprocal lattice in the pattern. Theoretical LEED–IV curves are calculated for a large number of geometrical models and these are compared with the experimental curves. The agreement is quantified by means of a reliability factor or R–factor. The closest this value to zero is, the more perfect the agreement between experimental and theoretical curves. In this way, the level of precision of the crystalline structure will depend on the smallest R–factor that can be achieved.
Pure metals with pure surfaces allow R–factor values of around 0.1. When moving to more complex structures, these values increase. The main reason for this gradually worse agreement between theoretical and experimental LEED-IV curves lies in the approximations in conventional LEED theory, which treats the atoms as perfect spheres with constant scattering potential in between. This description results in inaccurate scattering potential for more open surfaces and organic molecules. In consequence, a precision of 1-2 pm can be achieved for atoms in metal surfaces, whereas the positions of atoms within organic molecules are typically determined within ±10-20 pm. The values of the R-factor are usually between 0.2 and 0.5, where 0.2 represents a good agreement, 0.35 a mediocre agreement and 0.5 a poor agreement.
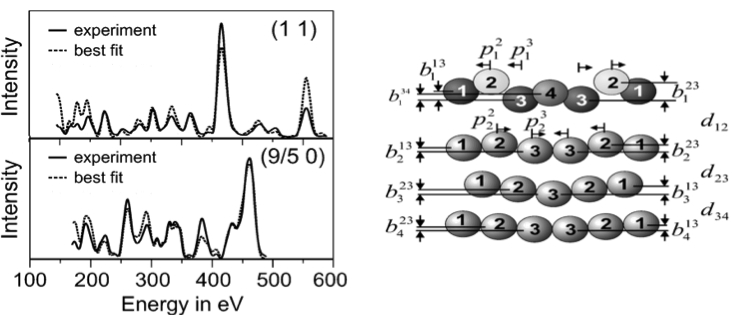
Figure \(\PageIndex{10}\) shows an example of a typical LEED–IV curve for Ir (100), which has a quasi-hexagonal unit cell. One can observe the parameters used to calculate the theoretical LEED–IV curve and the best-fitted curve obtained experimentally, which has an R–factor value of 0.144. The model used is also shown.