1.17: Principles of Gamma-ray Spectroscopy and Applications in Nuclear Forensics
- Page ID
- 55835
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Gamma-ray (γ-ray) spectroscopy is a quick and nondestructive analytical technique that can be used to identify various radioactive isotopes in a sample. In gamma-ray spectroscopy, the energy of incident gamma-rays is measured by a detector. By comparing the measured energy to the known energy of gamma-rays produced by radioisotopes, the identity of the emitter can be determined. This technique has many applications, particularly in situations where rapid nondestructive analysis is required.
Background Principles
Radioactive Decay
The field of chemistry typically concerns itself with the behavior and interactions of stable isotopes of the elements. However, elements can exist in numerous states which are not stable. For example, a nucleus can have too many neutrons for the number of protons it has or contrarily, it can have too few neutrons for the number of protons it has. Alternatively, the nuclei can exist in an excited state, wherein a nucleon is present in an energy state that is higher than the ground state. In all of these cases, the unstable state is at a higher energy state and the nucleus must undergo some kind of decay process to reduce that energy.
There are many types of radioactive decay, but type most relevant to gamma-ray spectroscopy is gamma decay. When a nucleus undergoes radioactive decay by α or β decay, the resultant nucleus produced by this process, often called the daughter nucleus, is frequently in an excited state. Similar to how electrons are found in discrete energy levels around a nucleus, nucleons are found in discrete energy levels within the nucleus. In γ decay, the excited nucleon decays to a lower energy state and the energy difference is emitted as a quantized photon. Because nuclear energy levels are discrete, the transitions between energy levels are fixed for a given transition. The photon emitted from a nuclear transition is known as a γ-ray.
Radioactive Decay Kinetics and Equilibria
Radioactive decay, with few exceptions, is independent of the physical conditions surrounding the radioisotope. As a result, the probability of decay at any given instant is constant for any given nucleus of that particular radioisotope. We can use calculus to see how the number of parent nuclei present varies with time. The time constant, λ, is a representation of the rate of decay for a given nuclei, \ref{1}.
\[ \frac{dN}{N}\ =\ -\lambda dt \label{1} \]
If the symbol N0 is used to represent the number of radioactive nuclei present at t = 0, then \ref{2} describes the number of nuclei present at some given time.
\[ N\ =\ N_{0}e^{-\lambda t} \label{2} \]
The same equation can be applied to the measurement of radiation with some sort of detector. The count rate will decrease from some initial count rate in the same manner that the number of nuclei will decrease from some initial number of nuclei.
The decay rate can also be represented in a way that is more easily understood. The equation describing half-life (t1/2) is shown in \ref{3}.
\[ t_{1/2}\ =\ \frac{ln\ 2}{\lambda } \label{3} \]
The half-life has units of time and is a measure of how long it takes for the number of radioactive nuclei in a given sample to decrease to half of the initial quantity. It provides a conceptually easy way to compare the decay rates of two radioisotopes. If one has a the same number of starting nuclei for two radioisotopes, one with a short half-life and one with a long half-life, then the count rate will be higher for the radioisotope with the short half-life, as many more decay events must happen per unit time in order for the half-life to be shorter.
When a radioisotope decays, the daughter product can also be radioactive. Depending upon the relative half-lives of the parent and daughter, several situations can arise: no equilibrium, a transient equilibrium, or a secular equilibrium. This module will not discuss the former two possibilities, as they are off less relevance to this particular discussion.
Secular equilibrium takes place when the half-life of the parent is much longer than the half-life of the daughter. In any arbitrary equilibrium, the ratio of atoms of each can be described as in \ref{4}.
\[ \frac{N_{P}}{N_{D}}\ =\ \frac{\lambda _{D}\ -\ \lambda _{P}}{\lambda _{P}} \label{4} \]
Because the half-life of the parent is much, much greater than the daughter, as the parent decays, the observed amount of activity changes very little.
\[ \frac{N_{P}}{N_{D}}\ =\ \frac{\lambda _{D}}{\lambda _{P}} \label{5} \]
This can be rearranged to show that the activity of the daughter should equal the activity of the parent.
\[ A_{P}\ =\ A_{D} \label{6} \]
Once this point is reached, the parent and the daughter are now in secular equilibrium with one another and the ratio of their activities should be fixed. One particularly useful application of this concept, to be discussed in more detail later, is in the analysis of the refinement level of long-lived radioisotopes that are relevant to trafficking.
Detectors
Scintillation Detector
A scintillation detector is one of several possible methods for detecting ionizing radiation. Scintillation is the process by which some material, be it a solid, liquid, or gas, emits light in response to incident ionizing radiation. In practice, this is used in the form of a single crystal of sodium iodide that is doped with a small amount of thallium, referred to as NaI(Tl). This crystal is coupled to a photomultiplier tube which converts the small flash of light into an electrical signal through the photoelectric effect. This electrical signal can then be detected by a computer.
Semiconductor Detector
A semiconductor accomplishes the same effect as a scintillation detector, conversion of gamma radiation into electrical pulses, except through a different route. In a semiconductor, there is a small energy gap between the valence band of electrons and the conduction band. When a semiconductor is hit with gamma-rays, the energy imparted by the gamma-ray is enough to promote electrons to the conduction band. This change in conductivity can be detected and a signal can be generated correspondingly. Germanium crystals doped with lithium, Ge(Li), and high-purity germanium (HPGe) detectors are among the most common types.
Advantages and Disadvantages
Each detector type has its own advantages and disadvantages. The NaI(Tl) detectors are generally inferior to Ge(Li) or HPGe detectors in many respects, but are superior to Ge(Li) or HPGe detectors in cost, ease of use, and durability. Germanium-based detectors generally have much higher resolution than NaI(Tl) detectors. Many small photopeaks are completely undetectable on NaI(Tl) detectors that are plainly visible on germanium detectors. However, Ge(Li) detectors must be kept at cryogenic temperatures for the entirety of their lifetime or else they rapidly because incapable of functioning as a gamma-ray detector. Sodium iodide detectors are much more portable and can even potentially be used in the field because they do not require cryogenic temperatures so long as the photopeak that is being investigated can be resolved from the surrounding peaks.
Gamma Spectrum Features
There are several dominant features that can be observed in a gamma spectrum. The dominant feature that will be seen is the photopeak. The photopeak is the peak that is generated when a gamma-ray is totally absorbed by the detector. Higher density detectors and larger detector sizes increase the probability of the gamma-ray being absorbed.
The second major feature that will be observed is that of the Compton edge and distribution. The Compton edge arises due to Compton Effect, wherein a portion of the energy of the gamma-ray is transferred to the semiconductor detector or the scintillator. This occurs when the relatively high energy gamma ray strikes a relatively low energy electron. There is a relatively sharp edge to the Compton edge that corresponds to the maximum amount of energy that can be transferred to the electron via this type of scattering. The broad peak lower in energy than the Compton edge is the Compton distribution and corresponds to the energies that result from a variety of scattering angles. A feature in Compton distribution is the backscatter peak. This peak is a result of the same effect but corresponds to the minimum energy amount of energy transferred. The sum of the energies of the Compton edge and the backscatter peak should yield the energy of the photopeak.
Another group of features in a gamma spectrum are the peaks that are associated with pair production. Pair production is the process by which a gamma ray of sufficiently high energy (>1.022 MeV) can produce an electron-positron pair. The electron and positron can annihilate and produce two 0.511 MeV gamma photons. If all three gamma rays, the original with its energy reduced by 1.022 MeV and the two annihilation gamma rays, are detected simultaneously, then a full energy peak is observed. If one of the annihilation gamma rays is not absorbed by the detector, then a peak that is equal to the full energy less 0.511 MeV is observed. This is known as an escape peak. If both annihilation gamma rays escape, then a full energy peak less 1.022 MeV is observed. This is known as a double escape peak.
Example of Experiments
Determination of Depleted Uranium
Natural uranium is composed mostly of 238U with low levels of 235U and 234U. In the process of making enriched uranium, uranium with a higher level of 235U, depleted uranium is produced. Depleted uranium is used in many applications particularly for its high density. Unfortunately, uranium is toxic and is a potential health hazard and is sometimes found in trafficked radioactive materials, so it is important to have a methodology for detection and analysis of it.
One easy method for this determination is achieved by examining the spectrum of the sample and comparing it qualitatively to the spectrum of a sample that is known to be natural uranium. This type of qualitative approach is not suitable for issues that are of concern to national security. Fortunately, the same approach can be used in a quantitative fashion by examining the ratios of various gamma-ray photopeaks.
The concept of a radioactive decay chain is important in this determination. In the case of 238U, it decays over many steps to 206Pb. In the process, it goes through 234mPa, 234Pa, and 234Th. These three isotopes have detectable gamma emissions that are capable of being used quantitatively. As can be seen in Table \(\PageIndex{1}\), the half-life of these three emitters is much less than the half-life of 238U. As a result, these should exist in secular equilibrium with 238U. Given this, the ratio of activity of 238U to each daughter products should be 1:1. They can thus be used as a surrogate for measuring 238U decay directly via gamma spectroscopy. The total activity of the 238U can be determined by \ref{7}, where A is the total activity of 238U, R is the count rate of the given daughter isotope, and B is the probability of decay via that mode. The count rate may need to be corrected for self-absorption of the sample is particularly thick. It may also need to be corrected for detector efficiency if the instrument does not have some sort of internal calibration.
\[ A= R/B \nonumber \]
| Isotope | Half-life |
| 238U | 4.5 x 10^{9} years |
| 234Th | 24.1 days |
| 234mPa | 1.17 minutes |
Example 1
Question
A gamma spectrum of a sample is obtained. The 63.29 keV photopeak associated with 234Th was found to have a count rate of 5.980 kBq. What is the total activity of 238U present in the sample?
Answer
234Th exists in secular equilibrium with 238U. The total activity of 234Th must be equal to the activity of the 238U. First, the observed activity must be converted to the total activity using Equation A=R/B. It is known that the emission probability for the 63.29 kEv gamma-ray for 234Th is 4.84%. Therefore, the total activity of 238U in the sample is 123.6 kBq.
The count rate of 235U can be observed directly with gamma spectroscopy. This can be converted, as was done in the case of 238U above, to the total activity of 235U present in the sample. Given that the natural abundances of 238U and 235U are known, the ratio of the expected activity of 238U to 235U can be calculated to be 21.72 : 1. If the calculated ratio of disintegration rates varies significantly from this expected value, then the sample can be determined to be depleted or enriched.
Example 2
Question
As shown above, the activity of 238U in a sample was calculated to be 123.6 kBq. If the gamma spectrum of this sample shows a count rate 23.73 kBq at the 185.72 keV photopeak for 235U, can this sample be considered enriched uranium? The emission probability for this photopeak is 57.2%.
Answer
As shown in the example above, the count rate can be converted to a total activity for 235U. This yields a total activity of 41.49 kBq for 235U. The ratio of activities of 238U and 235U can be calculated to be 2.979. This is lower than the expected ratio of 21.72, indicating that the 235U content of the sample greater than the natural abundance of 235U.
This type of calculation is not unique to 238U. It can be used in any circumstance where the ratio of two isotopes needs to be compared so long as the isotope itself or a daughter product it is in secular equilibrium with has a usable gamma-ray photopeak.
Determination of the Age of Highly-enriched Uranium
Particularly in the investigation of trafficked radioactive materials, particularly fissile materials, it is of interest to determine how long it has been since the sample was enriched. This can help provide an idea of the source of the fissile material—if it was enriched for the purpose of trade or if it was from cold war era enrichment, etc.
When uranium is enriched, 235U is concentrated in the enriched sample by removing it from natural uranium. This process will separate the uranium from its daughter products that it was in secular equilibrium with. In addition, when 235U is concentrated in the sample, 234U is also concentrated due to the particulars of the enrichment process. The 234U that ends up in the enriched sample will decay through several intermediates to 214Bi. By comparing the activities of 234U and 214Bi or 226Ra, the age of the sample can be determined.
\[ A_{Bi}\ =\ A_{Ra}\ =\ \frac{A_{U}}{2} \lambda _{Th}\lambda _{Ra} T^{2} \label{7} \]
In \ref{7}, ABi is the activity of 214Bi, ARais the activity of 226Ra, AU is the activity of 234U, λTh is the decay constant for 230Th, λRa is the decay constant for 226Ra, and T is the age of the sample. This is a simplified form of a more complicated equation that holds true over all practical sample ages (on the order of years) due to the very long half-lives of the isotopes in question. The results of this can be graphically plotted as they are in Figure \(\PageIndex{1}\).
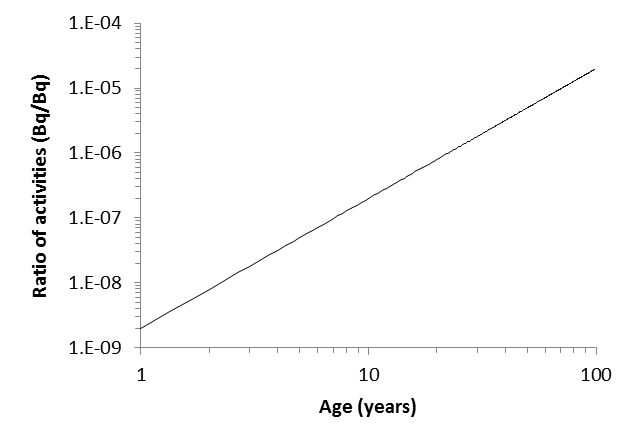
Example 3
Question
The gamma spectrum for a sample is obtained. The count rate of the 121 keV 234U photopeak is 4500 counts per second and the associated emission probability is 0.0342%. The count rate of the 609.3 keV 214Bi photopeak is 5.83 counts per second and the emission probability is 46.1%. How old is the sample?
Answer
The observed count rates can be converted to the total activities for each radionuclide. Doing so yields a total activity for 234U of 4386 kBq and a total activity for 214Bi of 12.65 Bq. This gives a ratio of 9.614 x 10-7. Using Figure \(\PageIndex{1}\), as graphed this indicates that the sample must have been enriched 22.0 years prior to analysis.


