3.2: Energy States and Transitions
- Page ID
- 111545
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Fluorescence only occurs after a chemical species has first been excited by electromagnetic radiation. The emission of radiation by a solid object heated in a flame (e.g., a piece of iron) is not fluorescence because the excitation has occurred thermally rather than through the absorption of electromagnetic radiation. Fluorescence can occur from species that have been excited by UV/VIS radiation. To consider what happens in the process of fluorescence, we need to think of the possible energy states for a ground and excited state system.
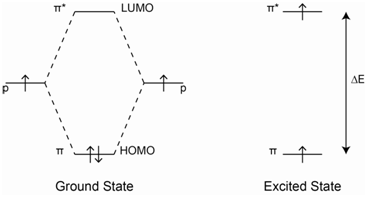
Draw an energy level diagram for a typical organic compound with \(\pi\) and \(\pi\) * orbitals.
Figure \(\PageIndex{1}\) represents the energy levels for a typical organic compound in which the \(\pi\) orbitals are full and the \(\pi\)* orbitals are empty.
Now consider the electron spin possibilities for the ground and excited state. Are there different possible ways to orient the spins (if so, these represent different spin states).
The ground state, which is shown on the left in Figure \(\PageIndex{1}\), has two electrons in the \(\pi\)-orbital. These two electrons must have opposite spins or else they would have the same four quantum numbers. Therefore, there is only one possible way to align the spins of the two electrons in the \(\pi\)-orbital.
The excited state has one electron in the \(\pi\)-orbital and one electron in the \(\pi\)*-orbital as shown in Figure \(\PageIndex{1}\). In this case, there are two possible ways we might align the spins. In one case, the electron in the \(\pi\)*-orbital could have the opposite spin of the electron in the \(\pi\)-orbital (e.g., the electrons have paired spins, even though they are in different orbitals – see Figure \(\PageIndex{2}\), middle diagram). In the other case, the electron in the \(\pi\)*-orbital could have a spin that is parallel with the electron in the \(\pi\)-orbital (see Figure \(\PageIndex{2}\) – far right diagram). In both cases, it does not matter which electron has spin-up and which has spin-down, the only important point is that in one case the two spins are opposite and in the other they are parallel. The energy level diagram in Figure \(\PageIndex{2}\) shows representations for the two possibilities.
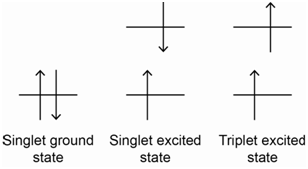
Do you think these different spin states have different energies?
Since they are different from each other (i.e., spins parallel versus spins paired), it makes sense that they would have different energies.
Which one do you expect to be lower in energy?
To answer this question, we have to think back to a rule we established with placing electrons into atomic or molecular orbitals that have the same energy (i.e., are degenerate). We learned that electrons go into degenerate orbitals with parallel spins and only pair up their spins when forced to do so (e.g., an atomic p3 configuration has three unpaired electrons with parallel spins; only when we added a fourth electron to make a p4 configuration do two of the electrons have paired spins). The rationale we gave for this observation is that configurations with parallel spins in degenerate orbitals are lower in energy than configurations with paired spins (i.e., it took energy to pair up electron spins). Applying this general concept to the situation above, we can reason that the configuration in which the electrons in the \(\pi\)- and \(\pi\)*-orbitals have parallel spins is lower in energy than the configuration in which the two electrons have paired spins. The energy level diagrams in Figure \(\PageIndex{3}\) show the lower energy of the configuration where the electrons have parallel spins.
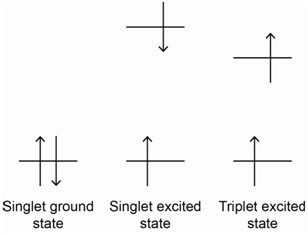
If the spin state is defined as (2S + 1) where S represents the total electronic spin for the system, try to come up with names for the ground and possible excited states for the system that are based on their spin state.
Remember that spin quantum numbers are either +½ or –½. S, the total electronic spin for the system, is the sum of the individual spin quantum numbers for all of the electrons.
In the case of the ground state, for every electron with a spin of +½ there is an electron with a spin of –½. Therefore, the value of S is zero. The spin state, which is 2S + 1, would have a value of 1.
In the case of the excited state in which the electrons have paired spins (+½ and –½), the value of S is also zero. Therefore, the spin state, which is 2S + 1, would have a value of 1.
In the case of the excited state in which the electrons have parallel spins (+½ and +½; by convention, we use the positive value of the spin for parallel spins when determining the spin state), the value of S is now one. Therefore, the spin state, which is 2S + 1, would have a value of 3.
The name we use to signify a system with a spin state of one is a singlet state. The name we use to signify a system with a spin state of three is a triplet state. Note that the ground state is a singlet state and that one of the excited states is a singlet state as well. We differentiate these by denoting the energy level with a number subscript. So the ground singlet state is denoted as S0 whereas the first excited state is denoted as S1. It is possible to excite a molecular species to higher electronic states so that higher energy S2, S3, etc. singlet states exist as well. The triplet state would be denoted as T1. There are also T2, T3, etc. as well. Now we can draw a more complex energy diagram for the molecule that shows different singlet and triplet levels (Figure \(\PageIndex{4}\)).
Draw a diagram of the energy levels for such a molecule. Draw arrows for the possible transitions that could occur for the molecule.
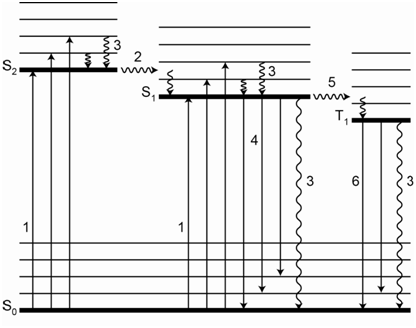
Note in Figure \(\PageIndex{4}\) how a triplet state is slightly lower in energy than the corresponding singlet state. Note as well that there are vibrational and rotational levels superimposed within the electronic states as we observed before when considering UV/VIS spectroscopy. The energy level diagram in Figure \(\PageIndex{4}\) shows the transitions that can occur within this manifold of energy states for an organic molecule. The transitions are numbered to facilitate our discussion of them.
Transition 1 (Absorption)
The transitions labeled with the number (1) in Figure \(\PageIndex{4}\) represent the process of absorption of incident radiation that promotes the molecule to an excited electronic state. The diagram shows the absorption process to the S1 and S2 states. It is also possible to excite the molecule to higher vibrational and rotational levels within the excited electronic states, so there are many possible absorption transitions. The following are equations that show the absorption of different frequencies of radiation needed to excite the molecule to S1 and S2.
\[\mathrm{S_0 + h\nu = S_1} \nonumber \]
\[\mathrm{S_0 + h\nu ’ = S_2} \nonumber \]
It is reasonable at first to think that there is an absorption transition that goes directly from the S0 to the T1 state. This is a transition that involves a spin-flip and it turns out that transitions that involve a spin-flip or change in spin state are forbidden, meaning that they do not happen (although, as we will soon see, sometimes transitions that are forbidden do happen). What is important here is that you will not get direct excitation from the S0 level to a higher energy triplet state. These transitions are truly forbidden and do not happen.
Transition 2 (Internal Conversion)
Internal conversion is the process in which an electron crosses over to another electronic state of the same spin multiplicity (e.g., singlet-to-singlet, triplet-to-triplet). The internal conversion in Figure \(\PageIndex{4}\) is from S2 to S1 and involves a crossover into a higher energy vibrational state of S1. It is also possible to have internal conversion from S1 to a higher vibrational level of S0.
Transition 3 (Radiationless decay – loss of energy as heat)
The transitions labeled with the number (3) in Figure \(\PageIndex{4}\) are known as radiationless decay or external conversion. These generally correspond to the loss of energy as heat to surrounding solvent or other solute molecules.
\[\mathrm{S_1 = S_0 + heat} \nonumber \]
\[\mathrm{T_1 = S_0 + heat} \nonumber \]
Note that systems in S1 and T1 can lose their extra energy as heat. Also, systems excited to higher energy vibrational and rotational states also lose their extra energy as heat. The energy diagram level in Figure \(\PageIndex{4}\) shows systems excited to higher vibrational levels of S1 and all of these will rapidly lose some of the extra energy as heat and drop down to the S1 level that is only electronically excited.
An important consideration that effects the various processes that take place for excited state systems is the lifetimes of the different excited states. The lifetime of a particular excited state (e.g. the S1 state) depends to some degree of the specific molecular species being considered and the orbitals involved, but measurements of excited state lifetimes for many different compounds allows us to provide ballpark numbers of the lifetimes of different excited states.
The lifetime of an electron in an S2 state is typically on the order of 10-15 second.
The lifetime of an electron in an S1 state depends on the energy levels involved. For a \(\pi\)-\(\pi\)* system, the lifetimes range from 10-7 to 10-9 second. For a n-\(\pi\)* system, the lifetimes range from 10-5 to 10-7 second. Since \(\pi\)-\(\pi\)* molecules are more commonly studied by fluorescence spectroscopy, S1 lifetimes are typically on the order of 10-8 second. While this is a small number on an absolute scale of numbers, note that it is a large number compared to the lifetimes of the S2 state.
The lifetime of a vibrational state is typically on the order of 10-12 second. Note that the lifetime of an electron in the S1 state is significantly longer than the lifetime of an electron in a vibrationally excited state of S1. That means that systems excited to vibrationally excited states of S1 rapidly lose heat (in 10-12 second) until reaching S1, where they then “pause” for 10-8 second.
Transition 4 (Fluorescence)
The transition labeled (4) in Figure \(\PageIndex{4}\) denotes the loss of energy from S1 as radiation. This process is known as fluorescence.
\[\mathrm{S_1 = S_0 + h\nu} \nonumber \]
Therefore, molecular fluorescence is a term used to describe a singlet-to-singlet transition in a system where the chemical species was first excited by absorption of electromagnetic radiation. Note that the diagram in Figure \(\PageIndex{4}\) does not show molecular fluorescence occurring from the S2 level. Fluorescence from the S2 state is extremely rare in molecules and there are only a few known systems where it occurs. Instead, what happens is that most molecules excited to energy states higher than S1 quickly (10-15 second) undergo an internal conversion to a high energy vibrational state of S1. They then rapidly lose the extra vibrational energy as heat and “pause” in the S1 state. From S1, they can either undergo fluorescence or undergo another internal conversion to a high energy vibrational state of S0 and then lose the energy as heat. The extent to which fluorescence or loss of heat occurs from S1 depends on particular features of the molecule and solution that we will discuss in more detail later in this unit.
An important aspect of fluorescence from the S1 state is that the molecule can end up in vibrationally excited states of S0, as shown in the diagram above. Therefore, fluorescence emission from an excited state molecule can occur at a variety of different wavelengths. Just like we talked about with absorbance and the probability of different transitions (reflected in the magnitude of the molar absorptivity), fluorescent transitions have different probabilities as well. In some molecules, the S1-to-S0 fluorescent transition is the most probable, whereas in other molecules the most probable fluorescent transition may involve a higher vibrational level of S1. A molecule ending up in a higher vibrational level of S1 after a fluorescent emission will quickly lose the extra energy as heat and drop down to S0.
So how do fluorescent light bulbs work? Inside the tube that makes up the bulb is a gas comprised of argon and a small amount of mercury. An electrical current that flows through the gas excites the mercury atoms causing them to emit light. This light is not fluorescence because the gaseous species was excited by an electrical current rather than radiation. The light emitted by the mercury strikes the white powdery coating on the inside of the glass tube and excites it. This coating then emits light. Since the coating was excited by light and emits light, it is a fluorescence emission.
Transition 5 (Intersystem crossing)
The transition labeled (5) in Figure \(\PageIndex{4}\) is referred to as intersystem crossing. Intersystem crossing involves a spin-flip of the excited state electron. Remember that the electron has “paused” in S1 for about 10-8 second. While there, it is possible for the species to interact with things in the matrix (e.g. collide with a solvent molecule) that can cause the electron in the ground and/or excited state to flip its spin. If the spin flip occurs, the molecule is now in a vibrationally excited level of T1 and it rapidly loses the extra vibrational energy as heat to drop down to the T1 electronic level.
What do you expect for the lifetime of an electron in the T1 state?
Earlier we had mentioned that transitions that involve a change in spin state are forbidden. Theoretically that means that an electron in the T1 state ought to be trapped there, because the only place for it to go on losing energy is to the S0 state. The effect of this is that electrons in the T1 state have a long lifetime, which can be on the order of 10-4 to 100 seconds.
There are two possible routes for an electron in the T1 state. One is that another spin flip can occur for one of the two electrons causing the spins to be paired. If this happens, the system is now in a high-energy vibrational state of S0 and the extra energy is lost rapidly as radiationless decay (transition 3) or heat to the surroundings.
Transition 6 (Phosphorescence)
The other possibility that can occur for a system in T1 is to emit a photon of radiation. Although, theoretically a forbidden process, it does happen for some molecules. This emission, which is labeled (6) in Figure \(\PageIndex{4}\), is known as phosphorescence. There are two common occasions where you have likely seen phosphorescence emission. One is from glow-in-the-dark stickers. The other is if you have ever turned off your television in a dark room and observed that the screen has a glow that takes a few seconds to die down. Phosphorescence is usually a weak emission from most substances.
Why is phosphorescence emission weak in most substances?
One reason why phosphorescence is usually weak is that it requires intersystem crossing and population of the T1 state. In many compounds, radiationless decay and/or fluorescence from the S1 state is preferable to intersystem crossing and not many of the species ever make it to the T1 state. Systems that happen to have a close match between the energy of the S1 state and a higher vibrational level of the T1 state may have relatively high rates of intersystem crossing. Compounds with non-bonding electrons often have higher degrees of intersystem crossing because the energy difference between the S1 and T1 states in these molecules is less. Paramagnetic substances such as oxygen gas (O2) promote intersystem crossing because the magnetic dipole of the unpaired electrons of oxygen can interact with the magnetic spin dipole of the electrons in the species under study, although the paramagnetism also diminishes phosphorescence from T1 as well. Heavy atoms such as Br and I in a molecule also tend to promote intersystem crossing.
A second reason why phosphorescence is often weak has to do with the long lifetime of the T1 state. The longer the species is in the excited state, the more collisions it has with surrounding molecules. Collisions tend to promote the loss of excess energy as radiationless decay. Such collisions are said to quench fluorescence or phosphorescence. Observable levels of phosphorescent emission will require that collisions in the sample be reduced to a minimum. Hence, phosphorescence is usually measured on solid substances. Glow-in-the-dark stickers are a solid material. Chemical substances dissolved in solution are usually cooled to the point that the sample is frozen into a solid glass to reduce collisions before recording the phosphorescence spectrum. This requires a solvent that freezes to a clear glass, something that can be difficult to achieve with water as it tends to expand and crack when frozen.
Which transition (\(\pi\)*-\(\pi\) or \(\pi\)*-n) would have a higher fluorescent intensity? Justify your answer.
There are two reasons why you would expect the \(\pi\)*-n transition to have a lower fluorescent intensity. The first is that the molar absorptivity of n-\(\pi\)* transitions is less than that of \(\pi\)-\(\pi\)* transitions. Fewer molecules are excited for the n-\(\pi\)* case, so fewer are available to fluoresce. The second is that the excited state lifetime of the n-\(\pi\)* state (10-5-10-7 second) is longer than that of the \(\pi\)-\(\pi\)* state (10-7-10-9 second). The longer lifetime means that more collisions and more collisional deactivation will occur for the n-\(\pi\)* system than the \(\pi\)-\(\pi\)* system.
Now that we understand the transitions that can occur in a system to produce fluorescence and phosphorescence occurs, we can examine the instrumental setup of a fluorescence spectrophotometer.


