2.1: Basic Terminology and Laws of Electricity

Last updated
Save as PDF

Page ID: 406376

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Current, \(I\), is a movement of charge over time and is expressed in amperes, \(A\), where 1 ampere is equivalent to 1 coulomb/sec. In this section we review the convention used to describe currents in electrical circuits and review four laws of electricity.

Conventional Currents

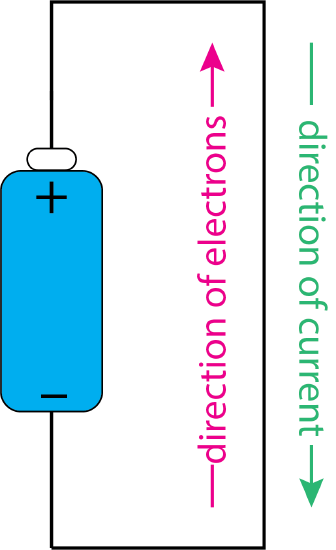
If we connect one end of a wire to the positive terminal of a battery and connect the other end to the negative terminal of the same battery, then electrons will move through the and a current will flow through the wire. The electrons move from the battery's negative terminal through the wire to the battery's positive terminal. The direction of the current, however, runs from the battery's positive terminal to the battery's negative terminal; that is, current is treated as if it is the movement of positive charge. This probably strikes you as odd, but it simply reflects the original understanding of current from a time before the electron was identified. Figure \(\PageIndex{1}\) shows the difference between these two ways of thinking about current.

Current in an electrical circuit. — Figure \(\PageIndex{1}\). Two descriptions of current in an electrical circuit. The convention for currents is

Laws of Electricity

There are four basic laws of electricity that are important to us in this chapter: Ohm's law, Kirchhoff's laws, and the power law. Let's take a brief look at each.

Ohm's Law

Ohm's law explains the relationship between current, \(I\), measured in amps (\(A\)), resistance, \(R\), measured in ohms (\(\Omega\)), and potential, \(V\), measured in volts (\(V\)), and is written as

\[V = I \times R \label{ohm} \]

The voltage is measured between any two points in a circuit using a voltmeter.

Kirchhoff's Two Laws

The first of Kirchoff's two laws states that the sum of the currents at any point in a circuit must equal zero.

\[ \sum{I} = 0 \label{kirch1} \]

The second law states that the sum of the voltages in a closed loop must equal zero.

\[ \sum{V} = 0 \label{kirch2} \]

Power Law

When a current passes through a resistor, the temperature of the resistor increases and power (energy per unit time) is lost. The amount of power lost, \(P\), is the product of current and voltage, with units of joules/sec

\[P = I \times V \label{power1} \]

or, substituting in Ohm's law (Equation \ref{ohm}), we can express power as

\[P = I^2 \times R = \frac{V^2}{R} \label{power} \]

Note

An excellent resource for this section and other sections in this chapter is Principles of Electronic Instrumentation by A. James Diefenderfer and published by W. B. Saunders Company, 1972.