1.3: The symmetry of crystals
- Page ID
- 352422
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the context of this chapter, you will also be invited to visit these sections...
- Symmetry elements
- The crystallographic restriction theorem
- Representation of crystal classes
- Representation of Laue groups
- Representation of Bravais lattices
About symmetry in general
Often we don't realize it, but we continuously live with symmetry... Symmetry is the consistency, the repetition of something in space and/or in time, as is shown in the examples below: a wall drawing, the petals of flowers, the two sides of a butterfly, the succession of night and day, a piece of music, etc.





Symmetry by repeating events: Day - Night - Day

Symmetry in music. A fragment from "Six unisono melodies" by Bartók.
(The diagram at the bottom represents the symmetrization of the one shown above)
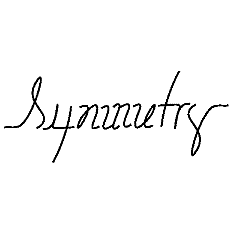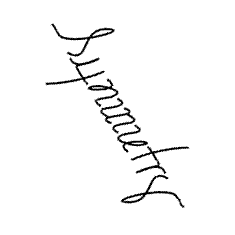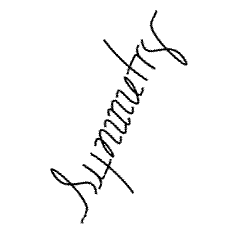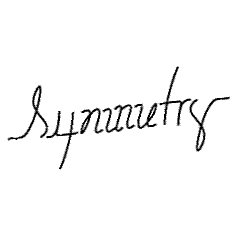
The word "Symmetry," carefully written with somewhat distorted letters, shows a two-fold axis (a rotation of 180 degrees) perpendicular to the screen.
The following sentence also serves to illustrate the concept of symmetry:
A MAN, A PLAN, A CANAL: PANAMA
where, if we forget the commas and the colon, it becomes:
AMANAPLANACANALPANAMA
which can be read from right to left with exactly the same meaning as above. It is a case similar to the "palindromic" numbers (232 or 679976).
There are many links in which the reader can find information on the concept of symmetry and we have selected some of them: symmetry and shape of space, some others in the context of crystallographic concepts, some with decorative patterns, or in the context of minerals. There is even an international society for the study of symmetry.
The essential knowledge on crystal morphology, symmetry elements and their combination to generate repetitive objects in space, were well established between the 17th and 19th Centuries, as stated elsewhere in these pages...
Specifically, in finite objects, there are a number of operations (elements of symmetry) describing repetitions. In the wall-drawing (shown above) we find translational operations (the motif is repeated by translation). The repetition of the petals in the flowers show us rotational operations (the motif is repeated by rotation) around a symmetry axis (or rotation axis). And, although not exactly, the symmetry shown in the phrase or in the music fragment (shown above), lead us to consider other symmetry operations known as symmetry planes (reflection planes, or mirror planes); the same operation that occurs when you look into a mirror. Similarly, for example, if we look at the relationship between the three-dimensional objects in some of the pictures shown below, we will discover a new element of symmetry called center of symmetry (or inversion center), which is an imaginary point between objects (or inside the object) as shown in some drawings below.
Generally speaking, and taking into account that pure translational operations are not strictly considered as symmetry operations, we can say that finite objects can contain themselves, or may be repeated (excluding translation) by the following symmetry elements:
- The identity operation is the simplest symmetry element of all -- it does nothing! But it is important because all objects at the very least have the identity element, and there are many objects that have no other symmetry elements.
- The reflection is the symmetry operation that occurs when we put an object in front of a mirror. The image is found perpendicular to the reflection plane and equidistant from that plane, on the opposite side of the plane. The resulting object can be distinguishable or indistinguishable from the original, normally distinguishable, as they cannot be superimposed. If the resulting object is indistinguishable from the original, is because the reflection plane is passing through the object.
- The inversion operation occurs through a single point called the inversion center. Each part of the object is moved along a straight line through the inversion center to a point at an equal distance from the inversion center. The resulting object can be distinguishable or indistinguishable from the original, normally distinguishable, as they cannot be superimposed. If the resulting object is indistinguishable from the original, is because the inversion center is inside the object.
- The rotation operations (both proper and improper) occur with respect to a line called rotation axis. a) A proper rotation is performed by rotating the object 360°/n, where n is the order of the axis. The resulting rotated object is always indistinguishable from the original. b) An improper rotation is performed by rotating the object 360°/n followed by a reflection through a plane perpendicular to the rotation axis. The resulting object can be distinguishable or indistinguishable from the original, normally distinguishable, as they cannot be superimposed. If the resulting object is indistinguishable from the original, is because the improper rotation axis is passing through the object.
In addition to the name of the symmetry elements, we use graphical and numerical symbols to represent them. For example, a rotation axis of order 2 (a binary axis) is represented by the number 2, and a reflection plane is represented by the letter m.
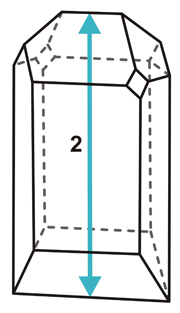

Left: Polyhedron showing a two-fold rotation axis (2) passing through the centers of the top and bottom edges
Right: Polyhedron showing a reflection plane (m) that relates (as a mirror does) the top to the bottom
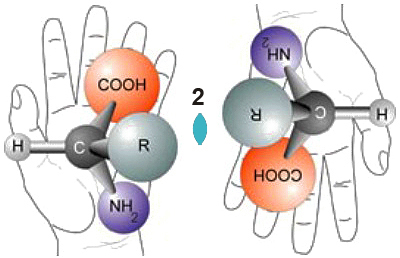
Hands and molecular models related by a twofold axis (2) perpendicular to the drawing plane

Hands and molecular models related through a mirror plane (m) perpendicular to the drawing plane

Hands (left and right) related through a center of symmetry
Two objects related by a center of symmetry and a polyhedron showing a center of symmetry in its center
The association of elements of rotation with centers or planes of symmetry generates new elements of symmetry called improper rotations.
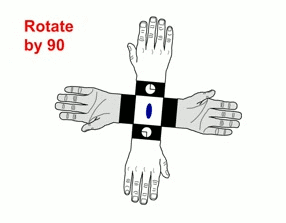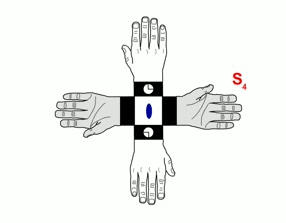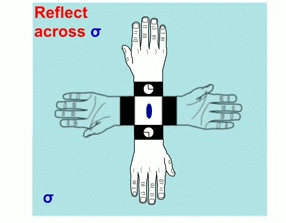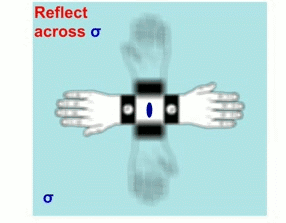
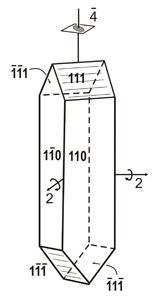
Left: A four-fold improper axis implies 90º rotations followed by reflection through a mirror plane perpendicular to the axis. (Animation taken from M. Kastner, T. Medlock & K. Brown, Univ. of Bucknell)
Right: Axis of improper rotation, shown vertically, in a crystal of urea. The meaning of numerical triplets shown will be discussed in another chapter.
Combining the rotation axes and the mirror planes with the characteristic translations of the crystals (which are shown below), new symmetry elements appear, with some "sliding" components: screw axes (or helicoidal axes) and glide planes.
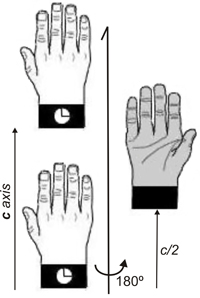
Twofold screw axis. A screw axis consists of a rotation followed by a translation
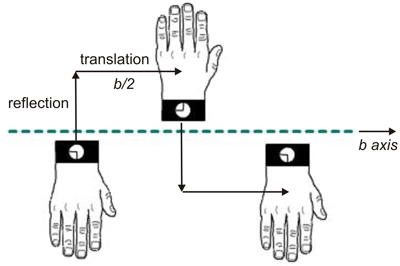
Glide plane. A glide plane consists of a reflection followed by a translation
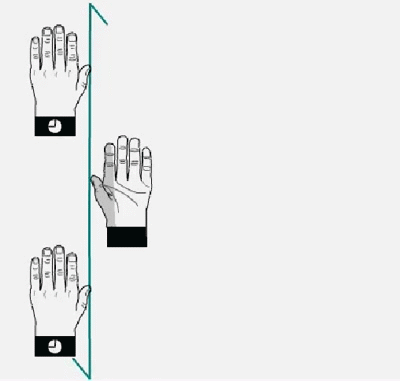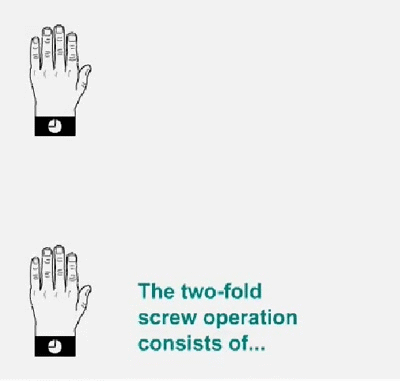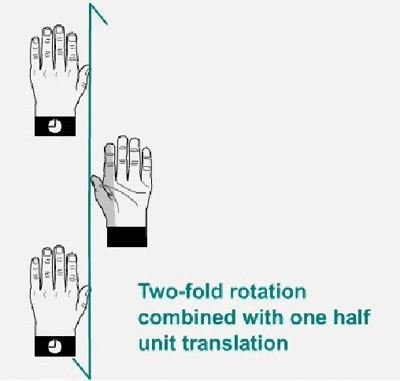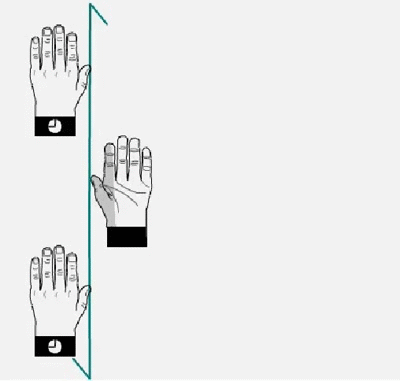
Twofold screw axis applied to a left hand. The hand rotates 180º and moves a half of the lattice translation in the direction of the screw axis, and so on. Note that the hand always remains as a left hand.
(Animation taken from M. Kastner, T. Medlock & K. Brown, Univ. of Bucknell)
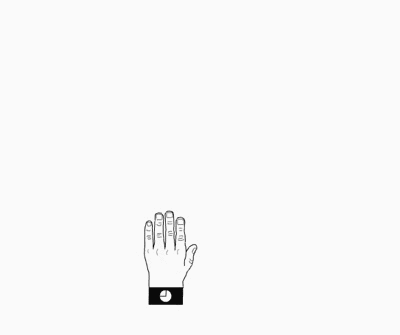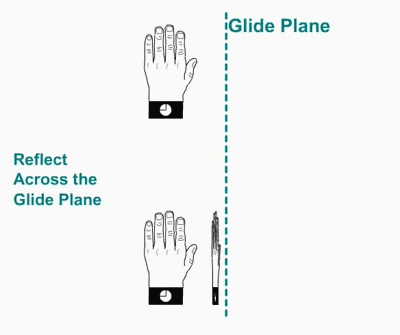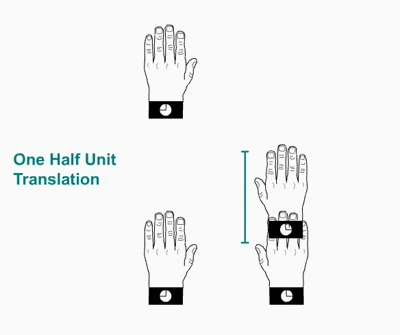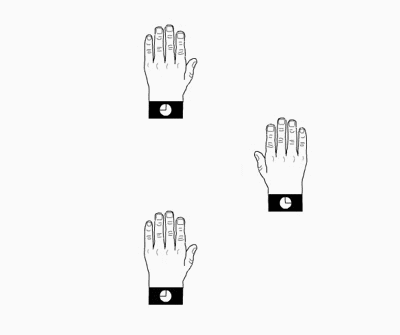
Glide plane.applied to a left hand. The left hand reflects on the plane, generating a right hand that moves a half of the lattice translation in the direction of the glide operation.
(Animation taken from M. Kastner, T. Medlock & K. Brown, Univ. of Bucknell)
The symmetry elements of types center or mirror plane relate objects in a peculiar way; the same way that our two hands are related one to the other: they are not superimposable. Objects which in themselves do not contain any of these symmetry elements (center or plane) are called chiral and their repetition through these elements (center or plane) produce objects that are called enantiomers with respect to the original ones. The mirror image of one of our hands is the enantiomer of the one we put in front of the mirror. Regarding the chirality of the crystals and of their building units (molecular or not), advanced readers should also consult the article by Howard D. Flack to be found through this link.

The mirror image of either of our hands is the enantiomer of the other hand. They are objects not superimposable and as they do not contain (in themselves) symmetry centers or symmetry planes, are called chiral objects.
Chiral molecules have different properties than their enantiomers and so it is important that we are able to differentiate them. The correct determination of the absolute configuration or absolute structure of a molecule (differentiation between enantiomers) can be done in a secure manner through X-ray diffraction only, but this will be explained in another chapter
Thus, any finite object (such as a quartz crystal, a chair or a flower) shows that certain parts of it are repeated by symmetry operations that go through a point of the object. This set of symmetry operations is known as a symmetry point group. The advanced reader has also the opportunity to visit the nice work on point group symmetry elements offered through these links:
- Dean H. Johnston from the Otterbein University, and
- Margaret Kastner, Timathy Medlock and Kristy Brown from the University of Bucknell.
A good general web site about symmetry in crystallography is offered by the Department of Chemistry and Biochemistry of the Oklahoma University.
Additionally, the reader can download (totally virus free!!!) and run on his own computer this Java application that, as an introduction to the symmetry of the polyhedra, that was developed by Gervais Chapuis and Nicolas Schöni (École Polytechnique Fédérale de Lausanne, Switzerland).
Symmetry in crystals
In crystals, the symmetry axes (rotation axes) can only be two-fold (2), three-fold (3), four-fold (4) or six-fold (6), depending on the number of times (order of rotation) that a motif can be repeated by a rotation operation, being transformed into a new state indistinguishable from its starting state. Thus, a rotation axis of order 3 (3-fold) produces 3 repetitions (copies) of the motif, one every 120 degrees (= 360/3) of rotation. If the reader wonders why only symmetry axes of order 2, 3, 4 and 6 can occur in crystals, and not 5-, 7-fold, etc., we recommend the explanations given in another section.
Improper rotations (rotations followed by reflection through a plane perpendicular to the rotational axis) are designated by the order of rotation, with a bar above that number.
The screw axes (or helicoidal axes, ie, symmetry axes involving rotation followed by a translation along the axis) are represented by the order of rotation, with an added subindex that quantifies the translation along the axis. Thus, a screw axis of type 62 means that in each of the six rotations an associated translation occurs of 2/6 of the axis of the elementary cell in that direction.
The mirror planes are represented by the letter m.
The glide planes (mirror planes involving reflexion and a translation parallel to the plane) are represented by the letters a, b, c, n or d, depending if the translation associated with the reflection is parallel to the reticular translations (a, b, c), parallel to the diagonal of a reticular plane (n), or parallel to a diagonal of the unit cell (d).
The letters and numbers that are used to represent the symmetry elements also have an equivalence with some graphic symbols.
But in order to keep talking about symmetry in crystals, it is necessary to introduce and remember the fundamental aspect that defines crystals, which is the periodic repetition by translation of motifs (atoms, molecules or ions). This repetition, which is illustrated in two dimensions with gray circles in the figure below, is derived from the mathematical concept of lattice that we will see more properly in another chapter.
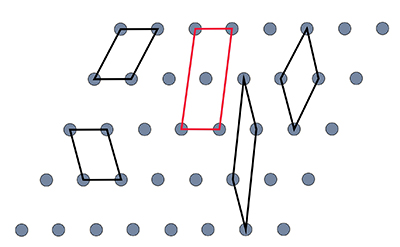
In a periodic and repetitive set of motifs (gray circles in the two-dimensional figure above) one can find infinite basic units (unit cells) vastly different in appearance and specification, the repetition of which generates the same mathematical lattice. Note that all represented unit cells delimited by black lines contain in total a single circle inside them, since each vertex contains a certain fraction of a circle inside the cell. These are called primitive cells. However, the cell delimited by red lines contains a total of two gray circles inside (one corresponding to the vertices and a complete one in the center). This type of unit cell is generically called non-primitive.
Periodic repetition, which is a characteristic of the internal structure of crystals, is represented by a set of translations in the three directions of space, so that crystals can be seen as the stacking of the same block in three dimensions. Each block, of a certain shape and size (but all of them being identical), is called a unit cell or elementary cell. Its size is determined by the length of its three edges (a, b, c) and the angles between them (alpha, beta, gamma: α, β, γ).


Stacking of unit cells forming an octahedral crystal and parameters which characterize the shape and size of an elementary cell (or unit cell)
As mentioned above, all symmetry elements passing through a point of a finite object, define the total symmetry of the object, which is known as the point group symmetry of the object. Obiously, the symmetry elements that imply any lattice translations (glide planes and screw axes), are not point group operations.
There are many symmetry point groups, but in crystals they must be consistent with the crystalline periodicity (translational periodicity). Thus, in crystals, only rotations (symmetry axes) of order 2, 3, 4 and 6 are possible, that is, only rotations of 180º (= 360/2), 120º (= 360/3), 90º (= 360/4) and 60º (= 360/6) are allowed. See also the crystallographic restriction theorem. Therefore, only 32 point groups are allowed in the crystalline state of matter. These 32 point groups are also known in Crystallography as the 32 crystal classes.
point group . crystal translational periodicity = 32 crystal classes
Graphic representation of the 32 crystal classes
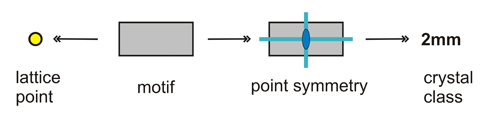
The motif, represented by a single brick, can also be represented by a lattice point. It shows the point symmetry 2mm
The next three tables show animated drawings about the 32 crystal classes, grouped in terms of the so called crystal system (left column), a classification mode in terms of minimal symmetry, as shown below.
 |
Links below illustrate the 32 crystal classes using some crystal morphologies These interactive animated drawings need the Java environment and therefore will not run with all browsers |
||||||
| Triclinic | 1 | 1 | |||||
| Monoclinic | 2 | m | 2/m | ||||
| Orthorhombic | 222 | mm2 | mmm | ||||
| Tetragonal | 4 | 4 | 4/m | 422 | 4mm | 42m | 4/mmm |
| Cubic | 23 | m3 | 432 | 43m | m3m | ||
| Trigonal | 3 | 3 | 32 | 3m | 3m | ||
| Hexagonal | 6 | 6 | 6/m | 622 | 6mm | 6m2 | 6/mmm |
 |
Links below illustrate the 32 crystal classes using some crystal morphologies These are non-interactive animated gifs obtained from the Java animations appearing in http://webmineral.com. They will run with all browsers |
||||||
| Triclinic | 1 | 1 | |||||
| Monoclinic | 2 | m | 2/m | ||||
| Orthorhombic | 222 | mm2 | mmm | ||||
| Tetragonal | 4 | 4 | 4/m | 422 | 4mm | 42m | 4/mmm |
| Cubic | 23 | m3 | 432 | 43m | m3m | ||
| Trigonal | 3 | 3 | 32 | 3m | 3m | ||
| Hexagonal | 6 | 6 | 6/m | 622 | 6mm | 6m2 | 6/mmm |
 |
Links below show animated displays of the symmetry elements in each of the 32 crystal classes: (taken from Marc De Graef) |
||||||
| Triclinic | 1 | 1 | |||||
| Monoclinic | 2 | m | 2/m | ||||
| Orthorhombic | 222 | mm2 | mmm | ||||
| Tetragonal | 4 | 4 | 4/m | 422 | 4mm | 42m | 4/mmm |
| Cubic | 23 | m3 | 432 | 43m | m3m | ||
| Trigonal | 3 | 3 | 32 | 3m | 3m | ||
| Hexagonal | 6 | 6 | 6/m | 622 | 6mm | 6m2 | 6/mmm |
Lluis Casas and Eugenia Estop, from the Department of Geology of the University of Barcelona, offer 32 pdf files which, in an interactive way, allow very easily playing with the 32 point groups through the symmetry of crystalline solids.
Additionally, the reader can download and run on his own computer this Java application that, as an introduction to the symmetry of the polyhedra, was developed by Gervais Chapuis and Nicolas Schöni (École Polytechnique Fédérale de Lausanne, Switzerland).
Alternatively, the interested reader can interactively view some typical polyhedra of the 7 crystal systems, through the Spanish Gemological Institute.
Of the 32 crystal classes, only 11 contain the operator center of symmetry, and these 11 centro-symmetric crystal classes are known as Laue groups.
crystal class . center of symmetry = 11 Laue groupsGraphic representation of the 11 Laue groups (centro-symmetric crystal classes)
In addition, the repetition modes by translation in crystals must be compatible with the possible point groups (the 32 crystal classes), and this is why we find only 14 types of translational lattices which are compatible with the crystal classes. These types of lattices (translational repetiton modes) are known as the Bravais lattices (you can see them here). The translational symmetry of an ordered distribution of 3-dimensional objects can be described by many types of lattices, but there is always one of them more suited to the object, ie: the one that best describes the symmetry of the object. As the lattices themselves have their own distribution of symmetry elements, we must fit them to the symmetry elements of the structure.
crystal translational periodicity . 32 crystal classes = 14 Bravais latticesGraphic representation of the 14 Bravais lattices
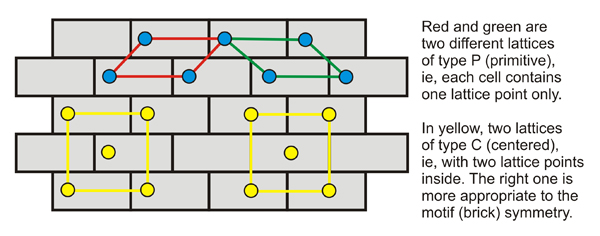
A brick wall can be structured with many different types of lattices, with different origins, and defining reticular points representing the brick. But there is a lattice that is more appropriate to the symmetry of the brick and to the way the bricks build the wall.
The adequacy of a lattice to the structure is illustrated in the two-dimensional examples shown below. In all three cases two different lattices are shown, one oblique and primitive and one rectangular and centered. In the first two cases, the rectangular lattices are the most appropriate ones. However, the deformation of the structure in the third example leads to metric relationships that make that the most appropriate lattice, the oblique primitive, hexagonal in this case.
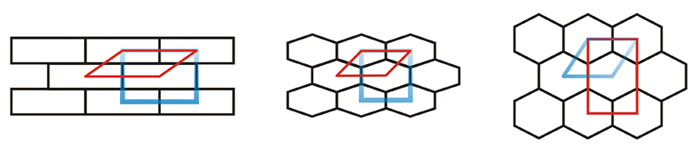
Adequacy of the lattice type to the structure. The blue lattice is the best one in each case.
Finally, combining the 32 crystal classes (crystallographic point groups) with the 14 Bravais lattices, we find up to 230 different ways to replicate a finite object (motif) in 3-dimensional space. These 230 ways to repeat patterns in space, which are compatible with the 32 crystal classes and with the 14 Bravais lattices, are called space groups, and represent the 230 different ways to fit the Bravais lattices to the symmetry of the objects. The interested reader should also consult the excellent work on the symmetry elements present in the space groups, offered by Margaret Kastner, Timathy Medlock and Kristy Brown through this link of the Bucknell University.
32 crystal classes + 14 Bravais lattices = 230 Space groups
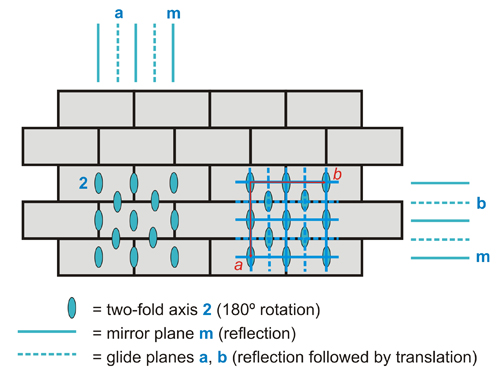
A wall of bricks showing the most appropriate lattice which best represents both the brick and its symmetry. Note that in this case the point symmetry of the brick and the point symmetry of the reticular point are coincident. The space group, considering the thickness of the brick, is Cmm2.
The 32 crystal classes, the 14 Bravais lattices and the 230 space groups can be classified, according to their hosted minimum symmetry, into 7 crystal systems. The minimum symmetry produces some restrictions in the metric values (distances and angles) which describe the shape and size of the lattice.
32 classes, 14 lattices, 230 space groups / crystal symmetry = 7 crystal systems
All this is summarized in the following table:
| Crystal classes (* Laue) |
Compatible crystal lattices and their symmetry |
Number of space groups |
Minimum symmetry | Metric restrictions | Crystal system |
| 1 1 * | P 1 |
2 | 1 or 1 | none | Triclinic |
| 2 m 2/m * | P C (I) 2/m |
13 | One 2 or 2 |
|
Monoclinic |
| 222 2mm mmm * | P C (A,B) I F mmm |
59 | Three 2 or 2 |
|
Orthorhombic |
| 4 4 4/m * 422 4mm 42m 4/mmm * |
P I 4/mmm |
68 | One 4 or 4 |
a=b |
Tetragonal |
| 3 3 * 32 3m 3m * |
P (R) 3m 6/mmm |
25 | One 3 or 3 |
a=b=c (or Hexagonal) |
Trigonal |
| 6 6 6m * 622 6mm 6m2 6/mmm * |
P 6/mmm |
27 | One 6 or 6 | a=b α=β=90 γ=120 |
Hexagonal |
| 23 m3 * 432 43m m3m * |
P I F m3m |
36 | Four 3 or 3 |
a=b=c |
Cubic |
| Total: 32, 11 *
|
14 independent | 230 | 7 |
The 230 crystallographic space groups are listed and described in the International Tables for X-ray Crystallography, where they are classified according to point groups and crystal systems. Chiral compounds that are prepared as a single enantiomer (for instance, biological molecules) can crystallize in only a subset of 65 space groups, those that do not have mirror and/or inversion symmetry operations.
A composition of part of the information contained in these tables is shown below, corresponding to the space group Cmm2, where C means that the structure is described in terms of a lattice centered on the faces separated by the c axis. The first m represents a mirror plane perpendicular to the a axis. The second m means another mirror plane (in this case perpendicular to the second main crystallographic direction), the b axis. The number 2 refers to the two-fold axis parallel to the third crystallographic direction, the c axis.
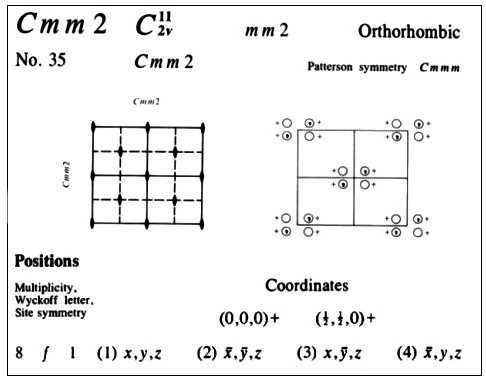
Summary of the information shown in the International Tables for X-ray Crystallography for the space group Cmm2
And this is another example for the space group P21/c, centrosymmetric and based on a primitive monoclinic lattice, as it appears in the International Tables for X-ray Crystallography

Summary of the information shown in the International Tables for X-ray Crystallography for the space group P21/c
The advanced reader can also consult:
- the teaching and learning package offered by the University of Cambridge on fundamental ideas and principles associated with the field of crystallography
- the hypertext book "Crystallographic Space Group Diagrams and Tables"
- the article by Dauter & Jaskolski entitled How to read and understand Volume A of International Tables for Crystallography
- the Bilbao crystallographic server, which is an excellent tool for the management of symmetry in crystallography, and/or
- the so-called space group decoder offered by Bernhard Rupp.
Crystallographers never get bored! Try to enjoy the beauty, looking for the symmetry of the objects around you, and particularly in the objects shown below ...
Look for possible unit-cells and symmetry elements in these structures made with bricks
(the solution is obtained clicking on the image)
There is a question that surely the readers will have considered... In this chapter we have shown elements of symmetry that operate inside the crystals, but we have not yet said how we can find out the existence of such operations, when in fact, and in the best of cases, we could only visualize the external habit of the crystals if they are well formed! Although we will not answer this question here, we can anticipate that this response will be given by the behavior of the crystals when we illuminate them with that special light that we know as X-rays, but this will be the subject of another chapter.
In any case, it doesn't end here! There are many more things to talk about. Go on.



