8.5: Using R for a Linear Regression Analysis

In Section 8.1 we used the data in the table below to work through the details of a linear regression analysis where values of \(x_i\) are the concentrations of analyte, \(C_A\), in a series of standard solutions, and where values of \(y_i\), are their measured signals, \(S\). Let’s use R to model this data using the equation for a straight-line.

\[y = \beta_0 + \beta_1 x \nonumber\]

Table \(\PageIndex{1}\): Calibration Data From Worked Example in Section 8.1.

\(x_i\)	\(y_i\)
0.000	0.00
0.100	12.36
0.200	24.83
0.300	35.91
0.400	48.79
0.500	60.42

Entering Data into R

To begin, we create two objects, one that contains the concentration of the standards and one that contains their corresponding signals.

conc = c(0, 0.1, 0.2, 0.3, 0.4, 0.5)

signal = c(0, 12.36, 24.83, 35.91, 48.79, 60.42)

Creating a Linear Model in R

A linear model in R is defined using the general syntax

dependent variable ~ independent variable(s)

For example, the syntax for a model with the equation \(y = \beta_0 + \beta_1 x\), where \(\beta_0\) and \(\beta_1\) are the model's adjustable parameters, is \(y \sim x\). Table \(\PageIndex{2}\) provides some additional examples where \(A\) and \(B\) are independent variables, such as the concentrations of two analytes, and \(y\) is a dependent variable, such as a measured signal.

Table \(\PageIndex{2}\): Syntax for Selected Linear Models in R.

model	syntax	comments on model
\(y = \beta_a A\)	\(y \sim 0 + A\)	straight-line forced through (0, 0)
\(y = \beta_0 + \beta_a A\)	\(y \sim A\)	stright-line with a y-intercept
\(y = \beta_0 + \beta_a A + \beta_b B\)	\(y \sim A + B\)	first-order in A and B
\(y = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB\)	\(y \sim A * B\)	first-order in A and B with AB interaction
\(y = \beta_0 + \beta_{ab} AB\)	\(y \sim A:B\)	AB interaction only
\(y = \beta_0 + \beta_a A + \beta_{aa} A^2\)	\(y \sim A + I(A\text{^2})\)	second-order polynomial

Note

The last formula in this table, \(y \sim A + I(A\text{^2})\), includes the I(), or AsIs function. One complication with writing formulas is that they use symbols that have different meanings in formulas than they have in a mathematical equation. For example, take the simple formula \(y \sim A + B\) that corresponds to the model \(y = \beta_0 + \beta_a A + \beta_b B\). Note that the plus sign here builds a formula that has an intercept and a term for \(A\) and a term for \(B\). But what if we wanted to build a model that used the sum of \(A\) and \(B\) as the variable. Wrapping \(A+B\) inside of the I() function accomplishes this; thus \(y \sim I(A + B)\) builds the model \(y = \beta_0 + \beta_{a+b} (A + B)\).

To create our model we use the lm() function—where lm stands for linear model—assigning the results to an object so that we can access them later.

calcurve = lm(signal ~ conc)

Evaluating the Linear Regression Model

To evaluate the results of a linear regression we need to examine the data and the regression line, and to review a statistical summary of the model. To examine our data and the regression line, we use the plot() function, first introduced in Chapter 3, which takes the following general form

plot(x, y, ...)

where x and y are the objects that contain our data and the ... allow for passing optional arguments to control the plot's style. To overlay the regression curve, we use the abline() function

abline(object, ...)

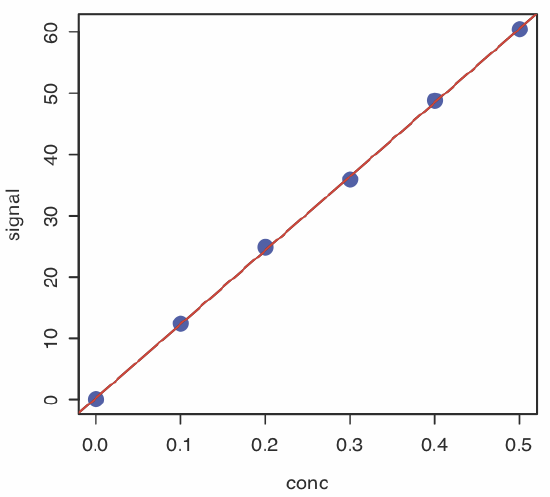
object is the object that contains the results of the linear regression model and the ... allow for passing optional arguments to control the model's style. Entering the commands

plot(conc, signal, pch = 19, col = "blue", cex = 2)

abline(calcurve, col = "red", lty = 2, lwd = 2)

creates the plot shown in Figure \(\PageIndex{1}\).

Note

The abline() function works only with a straight-line model.

Figure \(\PageIndex{1}\): Example of a regression plot in R showing the data (in blue) and the regression line (in red). You can customize your plot by adjusting the plot command’s optional arguments; see Chapter 3.3 for details.

To review a statistical summary of the regression model, we use the summary() function.

summary(calcurve)

The resulting output, which is shown below, contains three sections.

Call:

lm(formula = signal ~ conc)

Residuals:

1 2 3 4 5 6

-0.20857 0.08086 0.48029 -0.51029 0.29914 -0.14143

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 0.2086 0.2919 0.715 0.514

conc 120.7057 0.9641 125.205 2.44e-08 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.4033 on 4 degrees of freedom

Multiple R-squared: 0.9997, Adjusted R-squared: 0.9997

F-statistic: 1.568e+04 on 1 and 4 DF, p-value: 2.441e-08

The first section of this summary lists the residual errors. To examine a plot of the residual errors, use the command

plot(calcurve, which = 1)

which produces the result shown in Figure \(\PageIndex{2}\). Note that R plots the residuals against the predicted (fitted) values of y instead of against the known values of x, as we did in Section 8.1; the choice of how to plot the residuals is not critical. The line in Figure \(\PageIndex{2}\) is a smoothed fit of the residuals.

Note

The reason for including the argument which = 1 is not immediately obvious. When you use R’s plot() function on an object created using lm(), the default is to create four charts that summarize the model’s suitability. The first of these charts is the residual plot; thus, which = 1 limits the output to this plot.

Figure \(\PageIndex{2}\): Example showing R’s plot of a regression model’s residual error.

The second section of the summary provides estimate's for the model’s coefficients—the slope, \(\beta_1\), and the y-intercept, \(\beta_0\)—along with their respective standard deviations (Std. Error). The column t value and the column Pr(>|t|) are the p-values for the following t-tests.

slope: \(H_0 \text{: } \beta_1 = 0 \quad H_A \text{: } \beta_1 \neq 0\)

y-intercept: \(H_0 \text{: } \beta_0 = 0 \quad H_A \text{: } \beta_0 \neq 0\)

The results of these t-tests provide convincing evidence that the slope is not zero and no evidence that the y-intercept differs significantly from zero.

The last section of the summary provides the standard deviation about the regression (residual standard error), the square of the correlation coefficient (multiple R-squared), and the result of an F-test on the model’s ability to explain the variation in the y values.

The value for F-statistic is the result of an F-test of the following null and alternative hypotheses.

H₀: the regression model does not explain the variation in y

H_A: the regression model does explain the variation in y

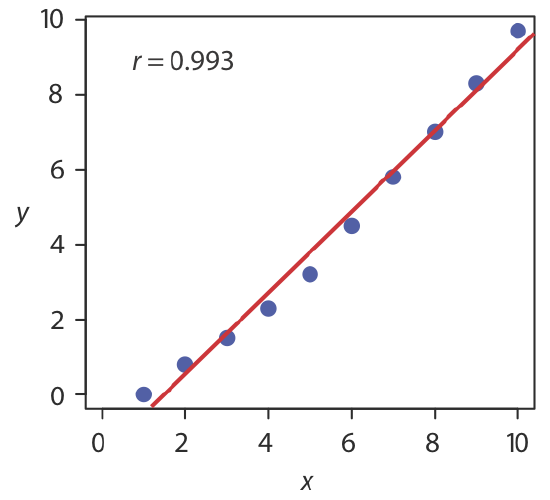
The value in the column for Significance F is the probability for retaining the null hypothesis. In this example, the probability is \(2.5 \times 10^{-8}\), which is strong evidence for rejecting the null hypothesis and accepting the regression model. As is the case with the correlation coefficient, a small value for the probability is a likely outcome for any calibration curve, even when the model is inappropriate. The probability for retaining the null hypothesis for the data in Figure \(\PageIndex{3}\), for example, is \(9.0 \times 10^{-5}\).

The correlation coefficient is a measure of the extent to which the regression model explains the variation in y. Values of r range from –1 to +1. The closer the correlation coefficient is to +1 or to –1, the better the model is at explaining the data. A correlation coefficient of 0 means there is no relationship between x and y. In developing the calculations for linear regression, we did not consider the correlation coefficient. There is a reason for this. For most straight-line calibration curves the correlation coefficient is very close to +1, typically 0.99 or better. There is a tendency, however, to put too much faith in the correlation coefficient’s significance, and to assume that an r greater than 0.99 means the linear regression model is appropriate. Figure \(\PageIndex{3}\) provides a useful counterexample. Although the regression line has a correlation coefficient of 0.993, the data clearly is curvilinear. The take-home lesson is simple: do not fall in love with the correlation coefficient!

Figure \(\PageIndex{3}\): Example of fitting a straight-line (in red) to curvilinear data (in blue).

Predicting the Uncertainty in \(x\) Given \(y\)

Although R's base installation does not include a command for predicting the uncertainty in the independent variable, \(x\), given a measured value for the dependent variable, \(y\), the chemCal package does. To use this package you need to install it by entering the following command.

install.packages("chemCal")

Once installed, which you need to do just once, you can access the package's functions by using the library() command.

library(chemCal)

The command for predicting the uncertainty in C_A is inverse.predict()and takes the following form for an unweighted linear regression

inverse.predict(object, newdata, alpha = value)

where object is the object that contains the regression model’s results, new-data is an object that contains one or more replicate values for the dependent variable and value is the numerical value for the significance level. Let’s use this command to complete the calibration curve example from Section 8.1 in which we determined the concentration of analyte in a sample using three replicate analyses. First, we create an object that contains the replicate measurements of the signal

rep_signal = c(29.32, 29.16, 29.51)

and then we complete the computation using the following command

inverse.predict(calcurve, rep_signal, alpha = 0.05)

which yields the results shown here

$Prediction

[1] 0.2412597

$`Standard Error`

[1] 0.002363588

$Confidence

[1] 0.006562373

$`Confidence Limits`

[1] 0.2346974 0.2478221

The analyte’s concentration, C_A, is given by the value $Prediction, and its standard deviation, \(s_{C_A}\), is shown as $`Standard Error`. The value for $Confidence is the confidence interval, \(\pm t s_{C_A}\), for the analyte’s concentration, and $`Confidence Limits` provides the lower limit and upper limit for the confidence interval for C_A.

Using R for a Weighted Linear Regression

R’s command for an unweighted linear regression also allows for a weighted linear regression if we include an additional argument, weights, whose value is an object that contains the weights.

lm(y ~ x, weights = object)

Let’s use this command to complete the weighted linear regression example in Section 8.2 First, we need to create an object that contains the weights, which in R are the reciprocals of the standard deviations in y, \((s_{y_i})^{-2}\). Using the data from the earlier example, we enter

syi = c(0.02, 0.02, 0.07, 0.13, 0.22, 0.33)

w =1/syi^2

to create the object, w, that contains the weights. The commands

weighted_calcurve = lm(signal ~ conc, weights = w)

summary(weighted_calcurve)

generate the following output.

Call:

lm(formula = signal ~ conc, weights = w)

Weighted Residuals:

1 2 3 4 5 6

-2.223 2.571 3.676 -7.129 -1.413 -2.864

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) 0.04446 0.08542 0.52 0.63

conc 122.64111 0.93590 131.04 2.03e-08 ***

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.639 on 4 degrees of freedom

Multiple R-squared: 0.9998, Adjusted R-squared: 0.9997

F-statistic: 1.717e+04 on 1 and 4 DF, p-value: 2.034e-08

Any difference between the results shown here and the results in Section 8.2 are the result of round-off errors in our earlier calculations.

Note

You may have noticed that this way of defining weights is different than that shown in Section 8.2 In deriving equations for a weighted linear regression, you can choose to normalize the sum of the weights to equal the number of points, or you can choose not to—the algorithm in R does not normalize the weights.

Using R for a Curvilinear Regression

As we see in this example, we can use R to model data that is not in the form of a straight-line by simply adjusting the linear model.

Example \(\PageIndex{1}\)

Use the data below to explore two models for the data in the table below, one using a straight-line, \(y = \beta_0 + \beta_1 x\), and one that is a second-order polynomial, \(y = \beta_0 + \beta_1 x + \beta_2 x^2\).

\(x_i\)	\(y_i\)
0.00	0.00
1.00	0.94
2.00	2.15
3.00	3.19
4.00	3.70
5.00	4.21

Solution

First, we create objects to store our data.

x = c(0, 1.00, 2.00, 3.00, 4.00, 5.00)
y = c(0, 0.94, 2.15, 3.19, 3.70, 4.21)

Next, we build our linear models for a straight-line and for a curvilinear fit to the data

straight_line = lm(y ~ x)

curvilinear = lm(y ~ x + I(x^2))

and plot the data and both linear models on the same plot. Because abline() only works for a straight-line, we use our curvilinear model to calculate sufficient values for x and y that we can use to plot the curvilinear model. Note that the coefficients for this model are stored in curvilinear$coefficients with the first value being \(\beta_0\), the second value being \(\beta_1\), and the third value being \(\beta_2\).

plot(x, y, pch = 19, col = "blue", ylim = c(0,5), xlab = "x", ylab = "y")

abline(straight_line, lwd = 2, col = "blue", lty = 2)

x_seq = seq(-0.5, 5.5, 0.01)

y_seq = curvilinear$coefficients[1] + curvilinear$coefficients[2] * x_seq + curvilinear$coefficients[3] * x_seq^2

lines(x_seq, y_seq, lwd = 2, col = "red", lty = 3)

legend(x = "topleft", legend = c("straight-line", "curvilinear"), col = c("blue", "red"), lty = c(2, 3), lwd = 2, bty = "n")

The resulting plot is shown here.