6.3: Using R to Model Properties of a Normal Distribution
- Page ID
- 220901
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Given a mean and a standard deviation, we can use R’s dnorm()function to plot the corresponding normal distribution
dnorm(x, mean, sd)
wheremeanis the value for \(\mu\),sdis the value for \(\sigma\), andxis a vector of values that spans the range of x-axis values we want to plot.
# define the mean and the standard deviation
mu = 12
sigma = 2
# create vector for values of x that span a sufficient range of
# standard deviations on either side of the mean; here we use values
# for x that are four standard deviations on either side of the mean
x = seq(4, 20, 0.01)
# use dnorm() to calculate probabilities for each x
y = dnorm(x, mean = mu, sd = sigma)
# plot normal distribution curve
plot(x, y, type = "l", lwd = 2, col = "blue", ylab = "probability", xlab = "x")
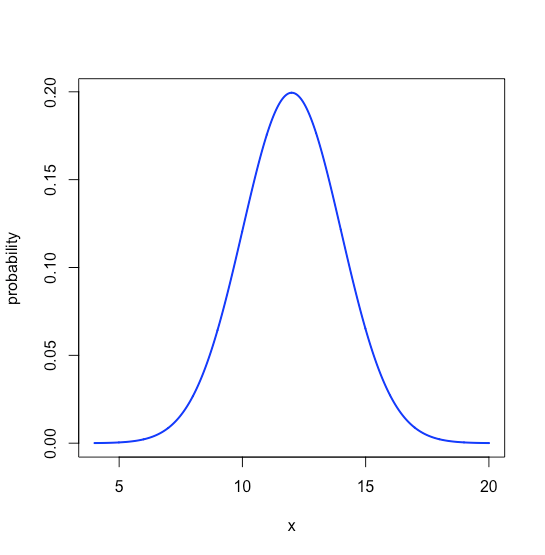
To annotate the normal distribution curve to show an area of interest to us, we use R’s polygon() function, as illustrated here for the normal distribution curve in Figure \(\PageIndex{1}\), showing the area that includes values between 8 and 15.
# define the mean and the standard deviation
mu = 12
sigma = 2
# create vector for values of x that span a sufficient range of
# standard deviations on either side of the mean; here we use values
# for x that are four standard deviations on either side of the mean
x = seq(4, 20, 0.01)
# use dnorm() to calculate probabilities for each x
y = dnorm(x, mean = mu, sd = sigma)
# plot normal distribution curve; the options xaxt = "i" and yaxt = "i"
# force the axes to begin and end at the limits of the data
plot(x, y, type = "l", lwd = 2, col = "ivory4", ylab = "probability", xlab = "x", xaxs = "i", yaxs = "i")
# create vector for values of x between a lower limit of 8 and an upper limit of 15
lowlim = 8
uplim = 15
dx = seq(lowlim, uplim, 0.01)
# use polygon to fill in area; x and y are vectors of x,y coordinates
# that define the shape that is then filled using the desired color
polygon(x = c(lowlim, dx, uplim), y = c(0, dnorm(dx, mean = 12, sd = 2), 0), border = NA, col = "ivory4")
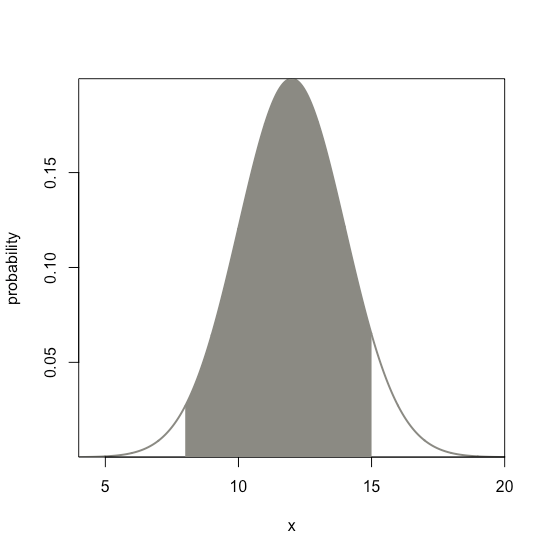
To find the probability of obtaining a value within the shaded are, we use R’spnorm()command
pnorm(q, mean, sd, lower.tail)
whereqis a limit of interest,meanis the value for \(\mu\),sdis the value for \(\sigma\), andlower.tailis a logical value that indicates whether we return the probability for values below the limit (lower.tail = TRUE) or for values above the limit (lower.tail = FALSE). For example, to find the probability of obtaining a result between 8 and 15, given \(\mu = 12\) and \(\sigma = 2\), we use the following lines of code.
# find probability of obtaining a result greater than 15
prob_greater15 = pnorm(15, mean = 12, sd = 2, lower.tail = FALSE)
# find probability of obtaining a result less than 8
prob_less8 = pnorm(8, mean = 12, sd = 2, lower.tail = TRUE)
# find probability of obtaining a result between 8 and 15
prob_between = 1 - prob_greater15 - prob_less8 # display results
prob_greater15
[1] 0.0668072
prob_less8
[1] 0.02275013
prob_between
[1] 0.9104427
Thus, 91.04% of values fall between the limits of 8 and 15.


