4.1: Ways to Summarize Data
- Page ID
- 219081
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Chapter 3 we used data collected from 30 bags of M&Ms to explore different ways to visualize data. In this chapter we consider several ways to summarize data using the net weights of the same bags of M&Ms. Here is the raw data.
| 49.287 | 48.870 | 51.250 | 48.692 | 48.777 | 46.405 |
| 49.693 | 49.391 | 48.196 | 47.326 | 50.974 | 50.081 |
| 47.841 | 48.377 | 47.004 | 50.037 | 48.599 | 48.625 |
| 48.395 | 51.730 | 50.405 | 47.305 | 49.477 | 48.027 |
| 48.212 | 51.682 | 50.802 | 49.055 | 46.577 | 48.317 |
Without completing any calculations, what conclusions can we make by just looking at this data? Here are a few:
- All net weights are greater than 46 g and less than 52 g.
- As we see in Figure \(\PageIndex{1}\), a box-and-whisker plot (overlaid with a stripchart) and a histogram suggest that the distribution of the net weights is reasonably symmetric.
- The absence of any points beyond the whiskers of the box-and-whisker plot suggests that there are no unusually large or unsually small net weights.
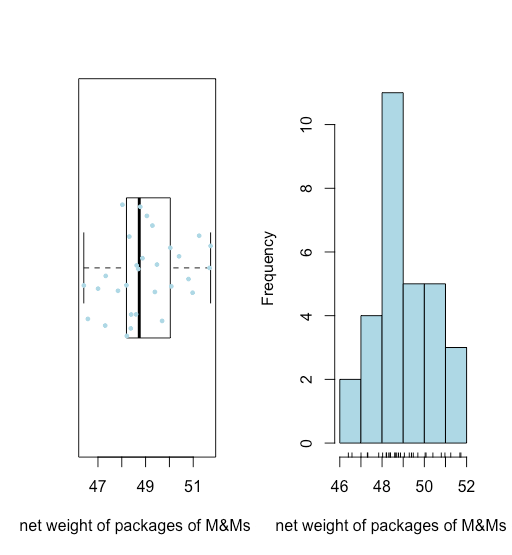
Both visualizations provide a good qualitative picture of the data, suggesting that the individual results are scattered around some central value with more results closer to that central value that at distance from it. Neither visualization, however, describes the data quantitatively. What we need is a convenient way to summarize the data by reporting where the data is centered and how varied the individual results are around that center.
Where is the Center?
There are two common ways to report the center of a data set: the mean and the median.
The mean, \(\overline{Y}\), is the numerical average obtained by adding together the results for all n observations and dividing by the number of observations
\[\overline{Y} = \frac{ \sum_{i = 1}^n Y_{i} } {n} = \frac{49.287 + 48.870 + \cdots + 48.317} {30} = 48.980 \text{ g} \nonumber\]
The median, \(\widetilde{Y}\), is the middle value after we order our observations from smallest-to-largest, as we show here for our data.
| 46.405 | 46.577 | 47.004 | 47.305 | 47.326 | 47.841 |
| 48.027 | 48.196 | 48.212 | 48.317 | 48.377 | 48.395 |
| 48.599 | 48.625 | 48.692 | 48.777 | 48.870 | 49.055 |
| 49.287 | 49.391 | 49.477 | 49.693 | 50.037 | 50.081 |
| 50.405 | 50.802 | 50.974 | 51.250 | 51.682 | 51.730 |
If we have an odd number of samples, then the median is simply the middle value, or
\[\widetilde{Y} = Y_{\frac{n + 1}{2}} \nonumber\]
where n is the number of samples. If, as is the case here, n is even, then
\[\widetilde{Y} = \frac {Y_{\frac{n}{2}} + Y_{\frac{n}{2}+1}} {2} = \frac {48.692 + 48.777}{2} = 48.734 \text{ g} \nonumber\]
When our data has a symmetrical distribution, as we believe is the case here, then the mean and the median will have similar values.
What is the Variation of the Data About the Center?
There are five common measures of the variation of data about its center: the variance, the standard deviation, the range, the interquartile range, and the median average difference.
The variance, s2, is an average squared deviation of the individual observations relative to the mean
\[s^{2} = \frac { \sum_{i = 1}^n \big(Y_{i} - \overline{Y} \big)^{2} } {n - 1} = \frac { \big(49.287 - 48.980\big)^{2} + \cdots + \big(48.317 - 48.980\big)^{2} } {30 - 1} = 2.052 \nonumber\]
and the standard deviation, s, is the square root of the variance, which gives it the same units as the mean.
\[s = \sqrt{\frac { \sum_{i = 1}^n \big(Y_{i} - \overline{Y} \big)^{2} } {n - 1}} = \sqrt{\frac { \big(49.287 - 48.980\big)^{2} + \cdots + \big(48.317 - 48.980\big)^{2} } {30 - 1}} = 1.432 \nonumber\]
The range, w, is the difference between the largest and the smallest value in our data set.
\[w = 51.730 \text{ g} - 46.405 \text{ g} = 5.325 \text{ g} \nonumber\]
The interquartile range, IQR, is the difference between the median of the bottom 25% of observations and the median of the top 25% of observations; that is, it provides a measure of the range of values that spans the middle 50% of observations. There is no single, standard formula for calculating the IQR, and different algorithms yield slightly different results. We will adopt the algorithm described here:
1. Divide the sorted data set in half; if there is an odd number of values, then remove the median for the complete data set. For our data, the lower half is
| 46.405 | 46.577 | 47.004 | 47.305 | 47.326 |
| 47.841 | 48.027 | 48.196 | 48.212 | 48.317 |
| 48.377 | 48.395 | 48.599 | 48.625 | 48.692 |
and the upper half is
| 48.777 | 48.870 | 49.055 | 49.287 | 49.391 |
| 49.477 | 49.693 | 50.037 | 50.081 | 50.405 |
| 50.802 | 50.974 | 51.250 | 51.682 | 51.730 |
2. Find FL, the median for the lower half of the data, which for our data is 48.196 g.
3. Find FU , the median for the upper half of the data, which for our data is 50.037 g.
4. The IQR is the difference between FU and FL.
\[F_{U} - F_{L} = 50.037 \text{ g} - 48.196 \text{ g} = 1.841 \text{ g} \nonumber\]
The median absolute deviation, MAD, is the median of the absolute deviations of each observation from the median of all observations. To find the MAD for our set of 30 net weights, we first subtract the median from each sample in Table \(\PageIndex{1}\).
| 0.5525 | 0.1355 | 2.5155 | -0.0425 | 0.0425 | -2.3295 |
| 0.9585 | 0.6565 | -0.5385 | -1.4085 | 2.2395 | 1.3465 |
| -0.8935 | -0.3575 | -1.7305 | 1.3025 | -0.1355 | -0.1095 |
| -0.3395 | 2.9955 | 1.6705 | -1.4295 | 0.7425 | -0.7075 |
| -0.5225 | 2.9475 | 2.0675 | 0.3205 | -2.1575 | -0.4175 |
Next we take the absolute value of each difference and sort them from smallest-to-largest.
| 0.0425 | 0.0425 | 0.1095 | 0.1355 | 0.1355 | 0.3205 |
| 0.3395 | 0.3575 | 0.4175 | 0.5225 | 0.5385 | 0.5525 |
| 0.6565 | 0.7075 | 0.7425 | 0.8935 | 0.9585 | 1.3025 |
| 1.3465 | 1.4085 | 1.4295 | 1.6705 | 1.7305 | 2.0675 |
| 2.1575 | 2.2395 | 2.3295 | 2.5155 | 2.9475 | 2.9955 |
Finally, we report the median for these sorted values as
\[\frac{0.7425 + 0.8935}{2} = 0.818 \nonumber \]
Robust vs. Non-Robust Measures of The Center and Variation About the Center
A good question to ask is why we might desire more than one way to report the center of our data and the variation in our data about the center. Suppose that the result for the last of our 30 samples was reported as 483.17 instead of 48.317. Whether this is an accidental shifting of the decimal point or a true result is not relevant to us here; what matters is its effect on what we report. Here is a summary of the effect of this one value on each of our ways of summarizing our data.
| statistic | original data | new data |
|---|---|---|
| mean | 48.980 | 63.475 |
| median | 48.734 | 48.824 |
| variance | 2.052 | 6285.938 |
| standard deviation | 1.433 | 79.280 |
| range | 5.325 | 436.765 |
| IQR | 1.841 | 1.885 |
| MAD | 0.818 | 0.926 |
Note that the mean, the variance, the standard deviation, and the range are very sensitive to the change in the last result, but the median, the IQR, and the MAD are not. The median, the IQR, and the MAD are considered robust statistics because they are less sensitive to an unusual result; the others are, of course, non-robust statistics. Both types of statistics have value to us, a point we will return to from time-to-time.


