Ligand Field Model for Electronic Structure of Coordination Complexes (Worksheet)
- Page ID
- 126994
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Template:HideTOCWork in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Learning Objectives
- Understand and apply the ligand field model (crystal field theory) in several geometries (octahedral, tetrahedral, tetragonal, square planar)
- Explain the color and magnetic behaviors of metal complexes
- Understand the spectrochemical series (both ligands and metals) in terms of bonding interactions
- Draw detailed and correct d-orbital splitting diagrams for octahedral, tetrahedral, tetragonal and square planar geometries
- Predict the low-spin, high-spin behavior and the number of unpaired electrons and the magnetic moment of a metal complex
- Relate the magnitude of the ligand field splitting to the color of the compound, the nature of the ligands and the geometry of the complex
Coordination complexes are unusual in that they are often beautifully colored, have characteristic colors for different coordination geometries and ligands, and have characteristic and varied magnetic properties. These properties arise from the energy splitting of the metal ion’s d-orbitals in the lower symmetry that the ligands impose. This feature combined with the number of d electrons of the metal determines which orbitals are occupied and the possible transitions and the number of unpaired electrons. The energy splitting of the d-orbitals can be understood in terms of several models, from the simple electrostatic charge model of crystal field to the sophisticated molecular orbital model of bonding. An understanding of the order of ligands according to their abilities to split the d-orbitals (the spectrochemical series) requires a basic understanding of both models. This activitiy guides you to explore and understand the models of ligand field splitting and bonding in metal complexes.
Post-activity assignment
Problems 4.20, 4.27 and 4.30
Plan
Work in groups of three to answer the following questions and problems.
Model 1: The d-orbitals in an octahedral field. See Figures 4.1 through 4.5 in Rodgers, pages 61 – 65. (Glen E. Rodgers, “Descriptive Inorganic, coordination and Solid-State Chemistry,” Brooks/Cole, Thompson Learning, USA, 2002, ISBN 0-12-592060-1).
Key Questions
- Draw five sketches of the x, y, z axes all oriented the same way with z axis vertical, x perpendicular in the plane of the page, and y at about a 30 degree angle to x going in and out of the page (as shown below). Use the drawings of the d-orbitals in Figure 4.1 to place a d orbital on each axis system. Label the drawings with the appropriate d orbital.
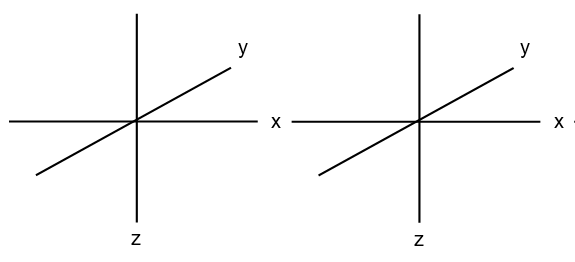
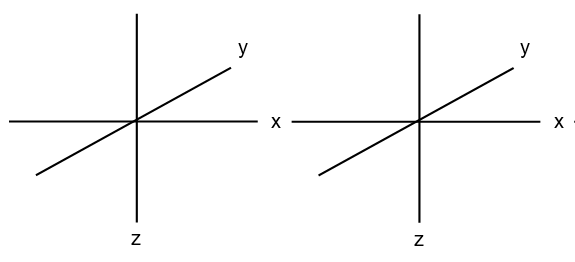
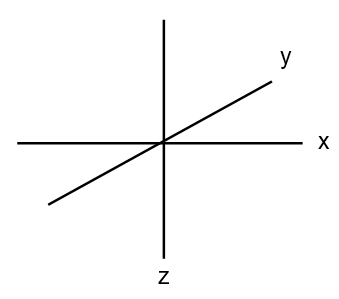
- Which d orbitals lie along the x, y or z-axes, and which lie between any two axes?
- Now for each of the five drawings, place the ligand charges on each of the axes (use 2- charges for this example), as shown in Figure 4.5. Which orbitals experience direct head-on interactions with the ligands that also lie along the axes?
- Which orbitals do not experience a direct head-on interaction with the ligands?
- Based on your answers in questions 3 and 4, divide the five d orbitals into two sets, the strong-interacting set and the weaker-interacting set.
- Given that the ligands are negative charges in this model and the d orbitals have electrons in them, which d orbitals are higher in energy in this model?
- Draw an approximate energy level diagram of the d-orbitals in the field of the six ligands in octahedral geometry.
Model 2: Figure 4.5 on page 65 of Rodgers.
- In this figure we see the energies of the d-orbitals about the “Barycenter” of the ligands. What is the significance of the Barycenter? Compare stages I and II for insight.
- What happens in stage III and why does the Barycenter remain at the same energy?
- In stage III the d-orbitals are split in energy. How does the splitting compare with your predictions from Model 1 above?
- Now we see in stage III that the splitting of the d-orbitals is labeled \(\Delta_{0}\) and the upper set is raised from the Barycenter by 3/5 \(\Delta_{0}\) and the lower set is lowered by 2/5 \(\Delta_{0}\). In terms of these energies what is the energy of the Barycenter?
- In stage IV, electrostatic attractions are added in to the energy of the system. What are these attractions? Is \(\Delta_{0}\) affected?
- What would be the affect on \(\Delta_{0}\) if the ligand charges were 1- instead of 2-? 3- instead of 2-? Using this point charge model is called Crystal Field Theory. It was the first theory used to understand the colors and magnetic behaviors of transition metal compounds.
Model 3: Figure 4.6 in Rodgers. Tetragonally distorted and square planar ligand fields
In this model the ligands on the z-axis are gradually removed from the complex by lengthening the M-L distance on the z-axis ligands while keeping the ligands in the x,y plane stationary. This sequence first lowers the symmetry from octahedral to D4h tetragonal, then ultimately to D4h square planar.
- Comparing octahedral, tetragonal and square planar energy diagrams, which orbitals fall in energy and which rise? Explain.
- Comparing octahedral, tetragonal and square planar energy diagrams, the orbitals are no longer in the sets of two and three of octahedral. Explain.
- Comparing octahedral and square planar energy diagrams, the dxy and dx2-y2 stay at the same energy difference, namely \(\Delta_{0}\). Why?
Model 4: Figures 4.7, 4.8 and 4.9 in Rodgers. Tetrahedral ligand field model.
This model is more difficult to visualize. You might not be able to predict the d-orbital splitting but you should be able to rationalize the given splitting in Figure 4.9.
- Expain in words the splitting of the d-orbitals into two sets and how these sets relate to the splitting in octahedral symmetry.
- In Figure 4.9 it states that \(\Delta_{t}\) = 4/9 \(\Delta_{0}\). Explain this equation qualitatively in words.
Reference
- Susan Jackels, Seattle University

