Ligand Field Model: Applications for Metal Complexes (Worksheet)
- Page ID
- 126996
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Learning Objectives
- Understand and apply the ligand field model (crystal field theory) in several geometries (octahedral, tetrahedral, tetragonal, square planar) (this was accomplished in Activity 5A)
- Explain the color and magnetic behaviors of metal complexes
- Understand the spectrochemical series (both ligands and metals) in terms of bonding interactions
- Draw detailed and correct d-orbital splitting diagrams for octahedral, tetrahedral, tetragonal and square planar geometries (this was done in Activity 5A)
- Predict the low-spin, high-spin behavior and the number of unpaired electrons and the magnetic moment of a metal complex
- Relate the magnitude of the ligand field splitting to the color of the compound, the nature of the ligands and the geometry of the complex
The properties of metal complexes can be understood from the energy splitting of the metal ion’s d-orbitals in the lower symmetry that the ligands impose. This feature combined with the number of d electrons of the metal determines which orbitals are occupied and the possible spectroscopic transitions and the number of unpaired electrons. The energy splitting of the d-orbitals can be understood in terms of several models, from the simple electrostatic charge model of crystal field to the sophisticated molecular orbital model of bonding. An understanding of the order of ligands according to their abilities to split the d-orbitals (the spectrochemical series) requires a basic understanding of both models. This activitiy guides you to explore and understand the applications of ligand field splitting in metal complexes.
Pre-Activity assignment
Problem 4.35
Post-activity assignment
Problems 4.31, 4.36, 4.37, 4.51 and 4.56
Plan
Work in groups of two or three to answer the following questions and problems.
Model 1: Table 4.1 Electronic Configurations and Crystal Field Stabilization Energies for Metal Ions in Octahedral Fields (page 71 of Rodgers) (Glen E. Rodgers, “Descriptive Inorganic, coordination and Solid-State Chemistry,” Brooks/Cole, Thompson Learning, USA, 2002, ISBN 0-12-592060-1).
Key Questions
- Table 4.1 lists the electronic configurations for three cases: Unsplit case, High-spin case and Low-spin case. On the figure below, you will find the labels for case 1, case 2 and case 3. Assign the three cases to the corresponding case in Table 4.1.
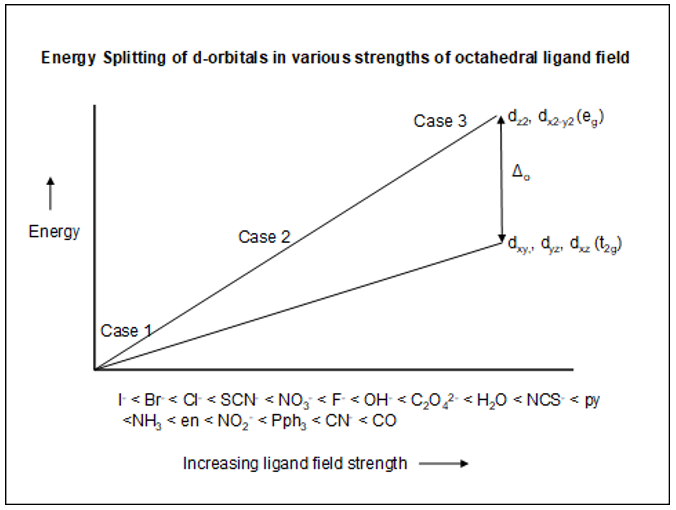
| Above Figure | Table 4.1 |
|---|---|
| Case 1 | _______ (Note: Case 1 is at the origin in the Figure) |
| Case 2 | _______ |
| Case 3 | _______ |
- In the Figure above, what happens to the d-orbital splitting as the ligand field strength increases?
- For the numbers of d electrons between 4 and 7 in Table 4.1, what is the difference between the High-spin and the Low-spin cases?
- Why is there only one case (listed in the middle between High-spin and Low-spin) for 1 – 3 d electrons and 8 – 10 electrons?
- What are the factors that determine whether a given complex, [ML6]n+, will have an electronic configuration in the High-spin or the Low-spin case?
- Write the definition of “pairing energy” here ___________________________________________________________________________
- The definition of Crystal Field Stabilization Energy (CFSE) is “the decrease in energy, relative to the unsplit case, of a coordination compound caused by the splitting of the metal d orbitals by a field of ligands. Use the diagram and equation below to calculate the CFSE for a complex having 6 d-electrons in both the high-spin and the low-spin cases. Note that high CFSE means that the complex is more stabilized with respect to the unsplit case.
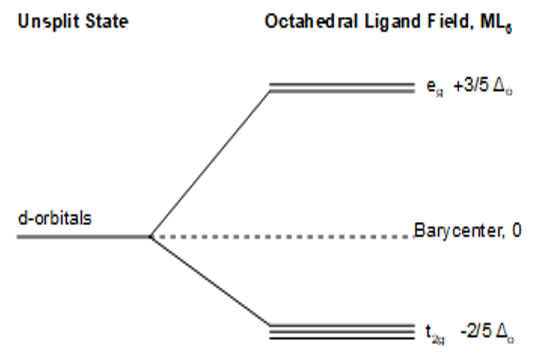
$$CFSE = nt_{2g} (\frac{2}{5} \Delta_{0}) + ne_{g} (- \frac{3}{5} \Delta_{0}) + qP\]
What is nt2g?
What is neg?
What is q?
What is P?
- In class we noted that the complexes with 3 d-electrons and 6 d-electrons (low spin) were most likely to have octahedral coordination. For which numbers of d-electrons is the CFSE greatest (assuming that P is about 40% of \(\Delta_{0}\)). For what other numbers of d-electrons would you expect octahedral coordination to be common? Why?
Model 2: Table 4.2 and the Spectrochemical Series on page 73 of Rodgers.
- What are the units used for \(\Delta_{0}\)? This is a common spectroscopic unit.
- Using the conversion factor 1000 cm-1 = 12.0 kJ/mole, calculate the CFSE of [Co(CN)6]3-.
- Using the text on pages 72 – 76, list the factors affecting the magnitude of the crystal field splitting, \(\Delta\):
- The spectrochemical series for common ligands is given below:
I- < Br- < Cl- < SCN- < NO3- < F- < OH- < C2O42- < H2O < NCS- < py <NH3 < en < NO2- < Pph3 < CN- < CO
Which ligand has the lowest ability to split the d-orbitals? The highest ability? - One series of ligands, namely, the halide anions, does seem to fit the crystal field model we explored in activity 5A. Explain how this series fits the model.
- Clearly, more than the crystal field model is needed to explain the entire series. The ligands in the middle of the series include some neutral molecules that function as Lewis bases in bonding to the metal ion. A) Using ammonia as an example, explain how ammonia functions as a Lewis base in bonding to a metal ion. B) What kind of bond is formed?
- The ligands at the high end of the series benefit from a covalent bonding effect called π-backbonding. Ligands that exhibit this effect have a lone pair that is donated to the metal accompanied by low-energy empty p (π) orbitals that can overlap with a metal d-orbital to create a “back bond” to the ligand from the metal. Draw a picture of a d-orbital (four-lobed type) overlapping with a ligand p orbital. See Figure 4.11 for guidance.
Reference
- Susan Jackels, Seattle University

