9: Ionic Structures (Worksheet)

Formulas for Ionic Compounds

Ionic Compounds (Empirical Formulas)

• Assuming that these ions are in closed shell (full octet), what would the charge be on each?

  Na K Ca Mg Al

  O F Cl S N

• Why do some ionic compounds occur in 1:1 ratios (like NaCl) and some in other ratios, such as lithium oxide (Li2O)? Keep in mind that Li₂O means that the ratio of Li⁺¹:O^-2 is 2:1.

• Assuming that each ion has a closed shell, propose a formula that balances the charges.

  sodium chloride potassium chloride calcium chloride

  sodium oxide calcium oxide aluminum oxide

• Assume the anion has a closed shell and the compound is neutral. What is the charge on each cation?

  ReO₃ IrO₂ TaN ZnCl₂

Structure of Solids Part II. Ionic Compounds

Ion Pairs to Lattices

To pair ions together releases energy:

Na⁺ + Cl^- ⟶ NaCl_(g) Ion pair + energy

energy = -589 kJ/mole

However, this pairing only accounts for some of the stabilization.

Na⁺ + Cl^- ⟶ NaCl_(g) Lattice + energy

energy = -774 kJ/mole

NaCl Solid Lattice:

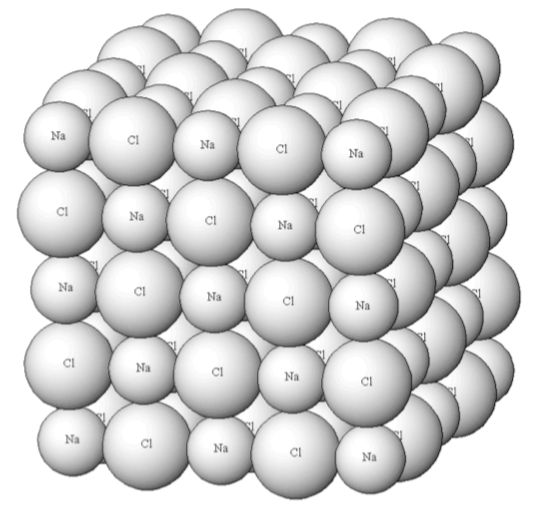
• Why does formation of the lattice improve stability of the ionic compound?

Ionic Packing Interstitial Holes

Many ionic compounds can be viewed as a packed array of anions with cations occupying interstitial holes in the structure

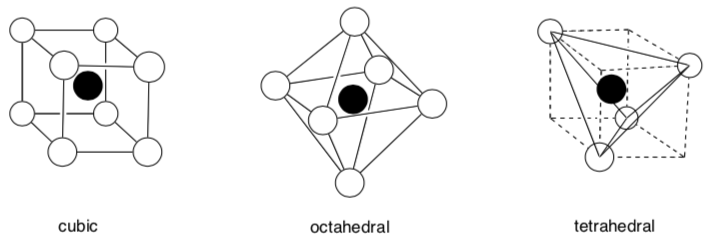
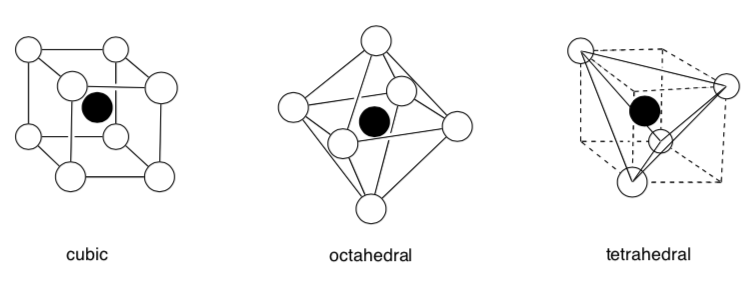
Coodination Geometry and Coordination Numbers

There are three common types of three-dimensional array of counterions in interstitial holes.

This is defined as the coordination geometry.

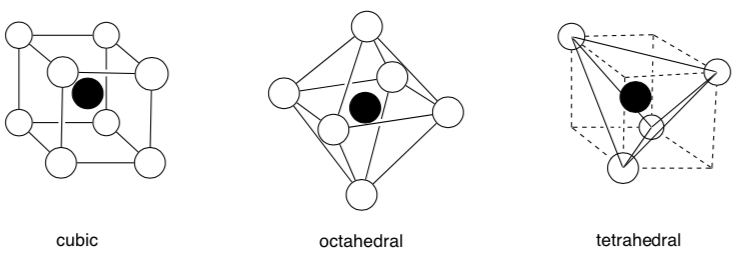
The number of neighboring atoms is called the coordination number.

• What is the coordination number for these geometries?

  • Cubic:

  • Octahedral:

  • Tetrahedral:

Simple Cubic Packing with a Counterion in Cubic Hole

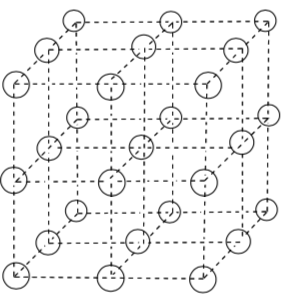
• Look at the bottom layer in this crystal. Does it look like a close packed layer or a simple cubic layer?

• Trace out the smallest repeating unit.

• Suppose these spheres were anions. Where would the cations go? In other

  words, where is a "hole" where the cations could fit?

• What would be the ratio of anions to cations in the repeating unit?

• How many anions would be in close contact with a cation in one of these holes?

• Which of the following geometries most closely resembles the "coordination environment" of the anion ("coordination environment" means the three- dimensional array of counterions around it).

Face Centered Cubic Packing with a Counterion in Tetrahedral Holes

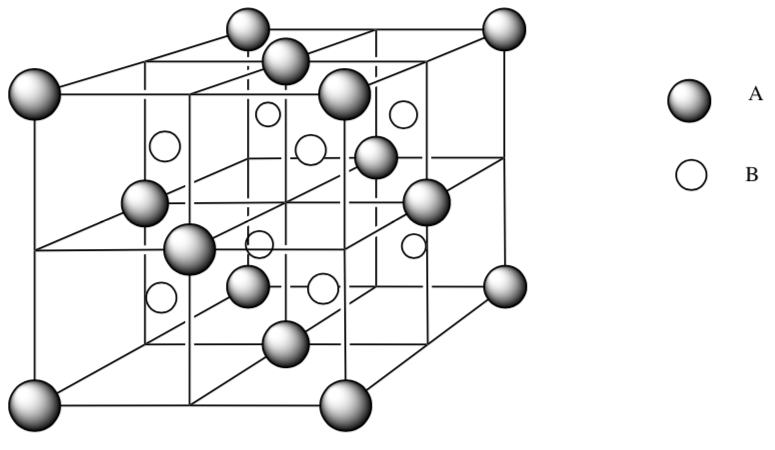
• Ions A () are packed in face centered cubic. How many atoms of ion A are fully in the unit cell? Show your work.

• Ions B () are placed in tetrahedral holes. Using a pen or highlighter, trace out the tetrahedral geometry.

• How many atoms of ion B are fully in the unit cell? Show your work.

• What is the ratio of ions A:ions B?

• What is the empirical formula for this ionic compound?

Face Centered Cubic Packing with a Counterion in Central Ocathedral Hole

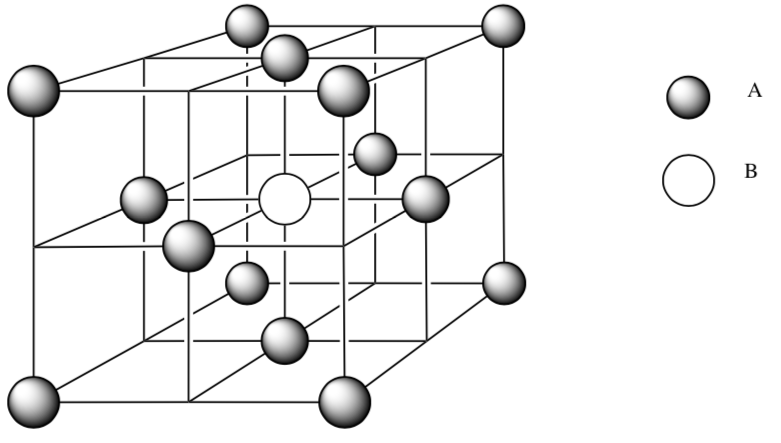
• Ions A () are packed in face centered cubic. How many atoms of ion A are fully in the unit cell? Show your work.

• Ions B () is placed in an octahedral hole. What is the coordination number for this ion?

• Using a pen or highlighter, trace out the atoms that are coordinating to ion B.

• How many atoms of ion B are fully in the unit cell? Show your work.

• What is the ratio of ions A:ions B?

• What is the empirical formula for this ionic compound?

Face Centered Cubic Packing with a Counterion in ALL Ocathedral Holes

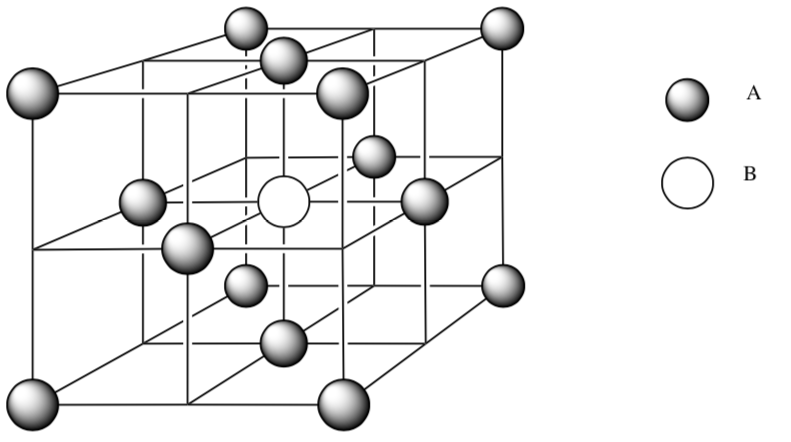
• Ions A () are packed in face centered cubic. How many atoms of ion A are fully in the unit cell? Show your work.

• Place more ion B () into all of the octahedral holes.

• How many atoms of ion B are fully in the unit cell? Show your work. An atom on an edge is 1⁄4 of an atom.

• What is the ratio of ions A:ions B?

• What is the empirical formula for this ionic compound?

Application Problems

For more practice with visualization of ionic solids and geometries: http://www.chm.davidson.edu/vce/crystals/index.html

1. Rock Salt

   The cations shown in the unit cell diagram below are Na+.

   • Draw in chloride (Cl-) anions into all the octahedral holes.

   • Determine the empirical formula of this compound.

   • What is the coordination number of sodium?

   • What is the coordination geometry of sodium?

   • What is the coordination number of chloride?

   • What is the coordination geometry of chloride?

     

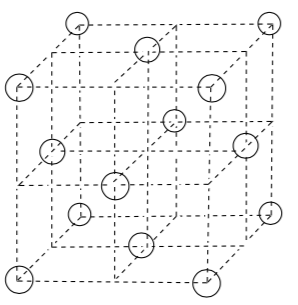
   The ions shown in the unit cell diagram below are Cl-.

   • Draw in sodium (Na+) cations into all the octahedral holes.

     

2. Packing for unknown salt

   • What is the packing type for atoms A?

   • How would you describe the interstitial hole occupied by atom B?

   • What is the empirical formula for this salt? Show your work.

     

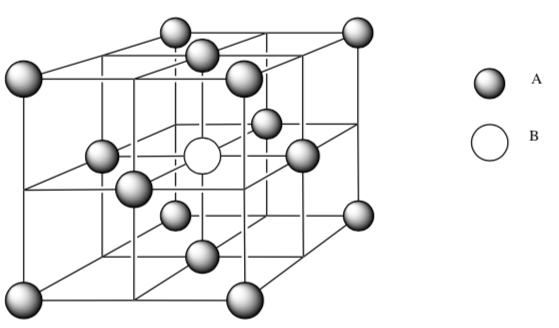
3. Packing for unknown salt

   • What is the packing type for atoms A?

   • How would you describe the interstitial holes occupied by atoms B?

   • What is the empirical formula for this salt? Show your work.

     

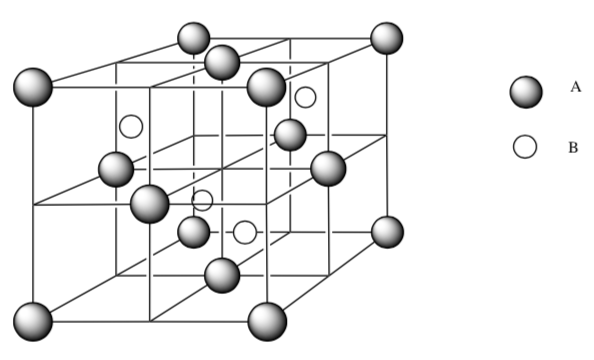
4. The cations shown in the face-centered unit cell diagram below are Ba⁺².

   • What is the packing type for atoms A?

   • How would you describe the interstitial holes occupied by atoms B?

   • What is the empirical formula for this salt? Show your work.

     

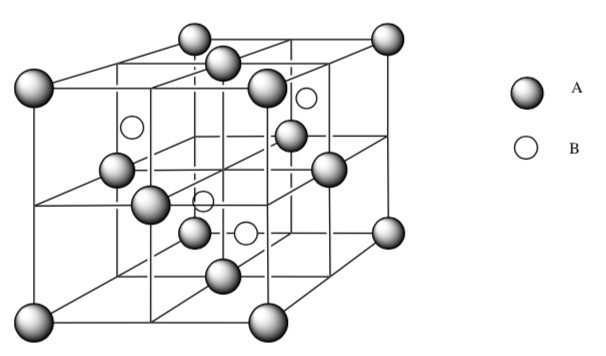
5. The cations shown in the face-centered unit cell diagram below are Ba⁺².

   • Draw in chloride (Cl-) anions into all the tetrahedral holes.

   • Determine the empirical formula of this compound.

   • What is the coordination number of the barium?

   • Does this empirical formula agree with your chemical intuition? Why or Why not?

     

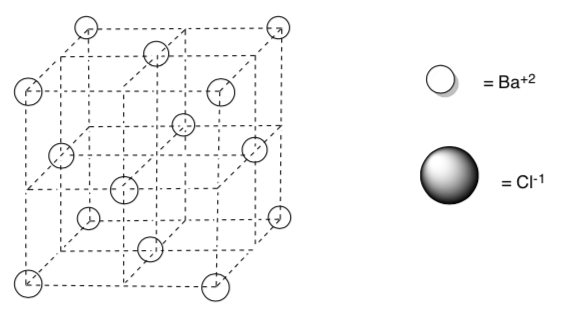
6. The ions shown in the face-centered cubic diagram below are sulfide, S^-2.

   • Draw in zinc cations into tetrahedral holes of the diagram below based on an empirical formula of ZnS.

   • How many of the holes are filled?

     

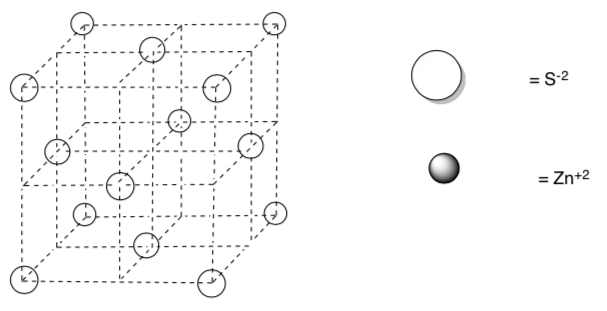
7. CsCl

   Coordination numbers: Cs=8; Cl=8

   Coordination Geometry: cubic

   • Draw in the chloride ions as simple cubic packing.

   • Add the cesium atoms so that the CN = 8.

     

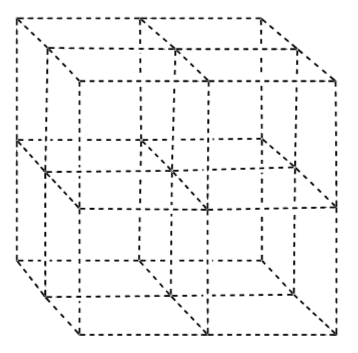
8. What is the formula for the compound that crystallizes with a cubic closest packed array of sulfur atoms, and that contains zinc ions in 1/8 of the tetrahedral holes and aluminum ions in 8 of the octahedral holes?

   • Draw the compound on the lattice below.

     

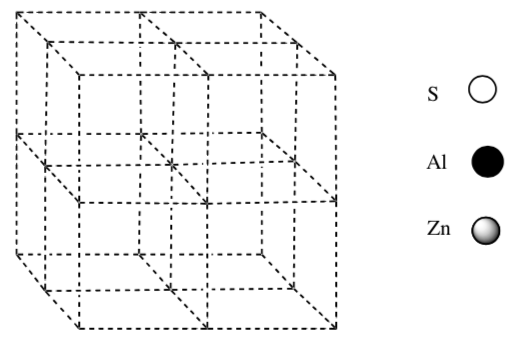
   • What is the empirical formula of this compound?

   • What is the Coordination Number for the aluminum?

   • What is the Coordination Geometry for the zinc?

9. A diagram of the unit cell for perovskite, a mineral containing calcium, titanium, and oxygen.

   • Determine the empirical formula of this compound.

   • What is the coordination geometry for the Ti?

     

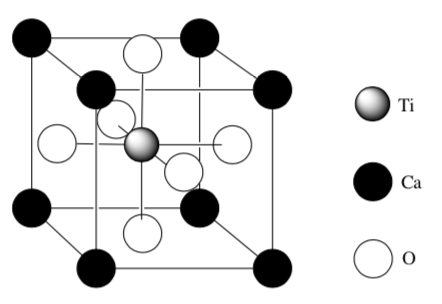
10. A diagram of the unit cell for nickel arsenide is shown below.

    • Determine the empirical formula of this compound.

    • Which packing model is used? (Note: This is a rhombus – not a cube)

      

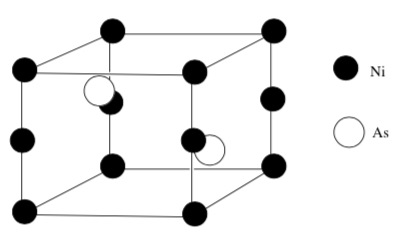
11. Ionic radii are determined experimentally from the unit cell dimensions, such as the edge length. Unfortunately, atoms do not always touch along an edge so that the unit cell length cannot be directly related to the ionic radius of an atom. An early attempt to develop a self-consistent set of ionic radii was made by Lande in 1920. He assumed that Li⁺ would be the smallest ion found in crystals. In compounds with the largest halide ions, the lithium ion would be too small to keep the halide ions from touching.

    1. LiI has a face-centered cubic structure. Assume that the I’s are close- packed. Draw a picture of the bottom of the unit cell showing the I’s just touching.

    2. NowdrawtheLi’ssotheyjustfitintheoctahedralholesinthebaseofthe unit cell.

    3. Experimentally, it was determined that the length of the unit cell edge of LiI was 600.0 pm. Use this information to calculate the ionic radius of iodide. (Hint—think Pythagorus.)

    4. Now, use the knowledge of the ionic radius of I^- to calculate the radius of Li⁺.

       Once we know these two radii, we can build up a self consistent set of many ionic radii. Even if the cations push the anions apart, cations and anions will still touch along the edge of a unit cell.

    5. Calculate the inonic radii for Na⁺ and Br^-, given that NaI and LiBr have the same structure as LiI but unit cell edge lengths of 647.3 and 550.1 pm , respectively.

Extra Lattice Templates

Predicting Packing for Ionic Solids

We are looking for a tightly packed structure with maximum contact between cations and anions to stabilize charge.

Usually the smaller ion is in the hole.

• Which is smaller? Cation or Anion

So we need to know the range of a size of a sphere that can be placed in a hole without pushing the spheres apart too much. This is shown in the face centered cubic packing shown below.

• Rank these packing situations in order of stability (least to most stable).

  

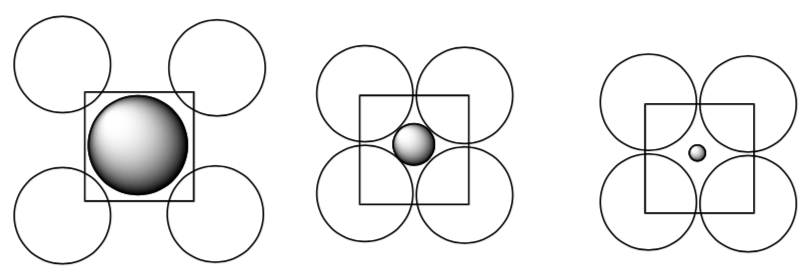
• Look at the three types of holes. Which could accommodate the largest cation?

  Keep in mind that higher coordination number = larger hole.

  

Doing some geometry, the size of the hole for the cation can be calculated. The Coordination Number is correlated to a ratio of the ionic radii:

rcation/ranion	Coordination Number	Hole for cation (smaller)
.225-.414	4	T etrahedral
.414-.732	6	Octahedral
.732-1.00	8	Cubic

Applications:

1. The ionic radii of Na+ and Cl- ions are 91 and 181 pm respectively.

   • Calculate the radii ratio of cation to anions.

   • What type of hole would the sodium prefer?

   • Does this match the packing structures that we did on previous pages?

2. The ionic radii of K+ and I- ions are 133 and 220 pm respectively.

   • Calculate the radii ratio of cation to anions.

   • What type of structure would you predict?

3. The ionic radii of Cs⁺ and Cl^- ions are 167 and 181 pm respectively.

   • Calculate the radii ratio of cation to anions.

   • What type of structure would you predict?

   • Draw this structure.

4. The ionic radii of Mg⁺² and O^-2 ions are 72 and 140 pm respectively.

   • Calculate the radii ratio of cation to anions.

   • What type of structure would you predict?

   • Draw this structure.

Beware!

Because there are other factors that affect packing, use radius ratios as a simple Predictional Tool, not as a means of rationalizing structures.

​​​​​​Summary

Summarize the new material on ionic packing.

• What holds the ionic compounds together?

Be sure to define the following terms. Use pictures to help understand the concepts. Draw a base layer for each type of packing.

• Empirical Formula

• Coordination Number

• Coordination Geometry

• T etrahedral Hole

• Octahedral Hole

• Cubic Hole

Explain how to solve the following type problems:

• Calculate the packing efficiency of a salt given ionic radii and need to know when atoms/ions touch.

• Predict the packing based on the ratio of ionic radii.

• Practice nomenclature of polyatomic ions (also on Sapling).

Cations (usually end in ium)

NH₄⁺ ammonium

(CH₃)₃C⁺ tert-butyl__________________

(or tert-butyl carbocation)

(CH₃)₄P⁺ tertra-methyl______________

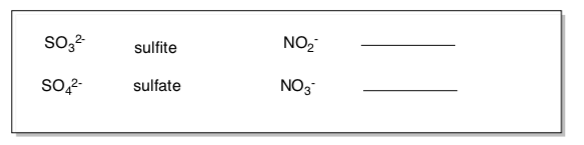
Anions (usually end in ite, ide or ate)

• What pattern do you notice for naming these oxo anions?

  

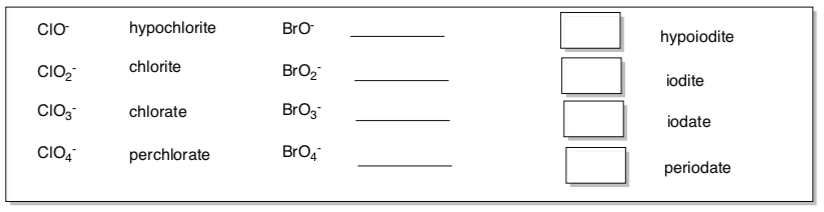
• What pattern do you notice for naming these oxo anions?

  

• What pattern do you notice for naming these anions?

  

Other Common Polyatomic Ions:

CH₃CO^2- acetate OH^- hydroxide

CN^- cyanide MnO₄^- permanganate

Properties of Ionic Compounds

Lattice Energy

The Lattice energy, U, is the amount of energy required to separate a mole of the solid (s) into a gas (g) of its ions.

Na⁺Cl^- (s) → Na⁺+ (g) + Cl^- (g) U (kJ/mol)

This quantity cannot be experimentally determined directly, but it can be estimated using Hess’ Law or calculated from the electrostatic consideration of its crystal structure.

Comparison of Lattice Energies (U in kJ/mol) of Some Salts:

Solid	U	Solid	U	Solid	U	Solid	U
LiF	1036	LiCl	853	LiBr	807	LiI	757
NaF	923	NaCl	786	NaBr	747	NaI	704
KF	821	KCl	715	KBr	682	KI	649
--
MgF2	2957	MgCl2	2526	MgBr2	2440	MgI2	2327

• On the table, use an arrow to indicate the increasing ionic radii on the table.

• On the table, circle all radii with +2 charge on the table.

The following trends determined from the data above:

• As the ionic radii of either the cation or anion increase, the lattice energies:

  Decrease or Increase

• The solids consisting of divalent (doubly charged) ions have:

  larger lattice energies or smaller lattice energies

• Propose a theory to explain these trends.

Lattice Energy Concept Problem

• Which of the following alkaline earth metal oxides has the larger lattice energy?

  

Unit cells to Lattice Energy

For simplicity, consider the ionic solids as a collection of positive and negative ions. In this simple view, appropriate number of cations and anions come together to form a solid.

The Madelung constant is used in determining the electrostatic potential of a single ion in a crystal by approximating the ions as point charges. For a given ratio of cation: anion, the Madelung constant is correlated to lattice energy.

Madelung Constants for different ionic solids

Ratio	Structural Type	CN	CN	Madelung Constant
			Cation	Anion
1:1
	Wurtzite (ZnS)	4	4	4
	ZnS	4	4	4
	NaCl	6	6	6
	CsCl	8	8	1.763
1:2
	beta-quartz	4	2	2.201
	CdCl2	6	3	2.244
	Rutile (TiO2)	6	3	2.408
	Fluorite (CaF2)	8	4	2.519

The following trends based on data above:

• As the coordination number increases, the Madelung Constant:

  Decreases or Increases

• The solids consisting of divalent ions have:

  larger Madelung Constants or smaller Madelung Constants

• Propose a theory to explain these trends.

Melting Points

The melting point of a solid is the temperature range at which it changes state from solid to liquid.

Salts	Melting point (K)	Lattice Energy (KJ/mol)
NaF	1074	786
Na2O	1407	2695
NaI	934	704
MgF2	1534	2957
BeO	2803	4443

The following trends based on data above:

• As the lattice energy increases, the melting point:

  Decreases or Increases

Summarize the following relationships:

• Charge to Lattice Energy

• Ionic Radius to Lattice Energy

• CN to Lattice Energy

• If you want to predict melting point, what factors would you need to consider?

• What happens to lattice energy when an impurity is present?

Solubility of Ionic Compounds

When dissolves in water, the cations and anions are separated. In the solution, the cations and anions are surrounded by water molecules.

NaCl(s) + H₂O(l) → Na⁺(aq) + Cl^-(aq)

The ”(aq)” after the ion indicates that each ion of that type is surrounded by several water molecules.

Sometimes not all of the ions dissolve.

• Draw a cartoon of an ionic compound that partially dissolves in water.

Precipitation Reactions

In a precipitation reaction, a solid product is formed from two electrolyte solutions.

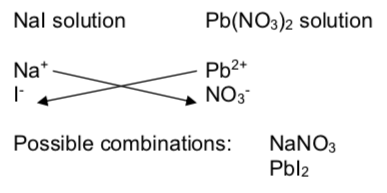
Combined solutions of ionic compounds provide the following data:

Precipitation of Ionic Compounds

Solutions T ested	KNO3	KBr	K2SO4	K2CO3	K2C2O4	K3PO4
NaCl
CaCl2			P	P	P	P
LiCl
BaCl2			P	P	P	P

Note: P means a precipitate is formed; a blank means that the compounds are soluble.

Trends:

• Ionic compounds containing a Group I cation are likely to be:

  Soluble Insoluble

• Ionic compounds containing a halide ion or nitrate ion are likely to be:

  Soluble Insoluble

• Ionic compounds containing a monopositive cation and a mononegative anion are likely to be:

  Soluble Insoluble

• Ionic compounds containing a multiply charged cation and a multiply charged anion are likely to be:

  Soluble Insoluble

Summary:

When the ionic compounds contain multiply charged atoms, the lattice energies are ___________ (stronger/weaker) therefore making these compounds ___________ (more/less) soluble in water.

Practice Problems

• How does the solubility of ionic compounds containing multiply charged anions (SO₄^2-. CO₃^2-, C₂O₄^2- and PO₄^3-) compare to those containing singly charged anions? Why?

• As the charge of the cation and anion increases, solubility of ionic compounds: Increase Decrease

• How are solubility and lattice energy related?

• Use Coulomb’s law, lattice energy and packing to explain the statements above.

• Why do you think alkali halides like sodium chloride (NaCl) are readily available in seawater, but aluminum oxide (Al₂O₃) is not?

• We need solid materials to give structural support to otherwise mushy, watery organisms. Why is bone mineral made of (roughly speaking) calcium phosphate [Ca₃(PO₄)₂] and not solid sodium chloride?

Applications of Packing and Properties

1. Spinels (Balas Rubies)

   The spinel crystal lattice has an empirical formula of A²⁺B₂³⁺O₄^2-. The original spinel mineral was identified as containing Al, O, and Mg.

   Magnetic atoms/molecules result from the presence of unpaired electrons. In some minerals with a spinel crystal structure, the Mg ions are replaced by Fe ions of the same charge.

   In some minerals with a spinel crystal structure, the Mg ions are replaced by Fe ions of the same charge.

   • Write the empirical formula for this original spinel.

   • Part of the spinel unit cell involves the tetrahedral coordination of a magnesium ion by four oxygen ions. In the empty lattice given below, draw in the Mg and O ions.

     

   • Show the electron configurations for the magnesium ion and the iron ion.

   • Explain why the structure containing the Mg cations is non-magnetic while the structure containing the Fe cations is magnetic.

2. Nanosensors: Ionic Conductors

   “Almost” no ionic compounds conduct electricity as solids. One that does so is used as the oxygen sensor in your car. It is based on ZrO₂.

   This compound can be viewed as a face-centered array of Zr ions.

   A unit cell must be electrically neutral.

   In the oxygen sensor, 1⁄4 of the Zr’s have been replaced with Ca. (This is called “doping”.)

   The unit cell must remain neutral.

   The presence of these vacancies is required for conductivity in the solid state.

   In an oxygen sensor, there is a platinum electrode on either side of a crystal of the Ca-doped zirconium oxide. The platinum can adsorb oxygen from the air and convert it into oxide ion, which can migrate though the structure. The platinum electrode draws a current (electrons) to carry out this transformation.

   When oxide ions get to the other side of the material, they are converted back into oxygen.

   This current creates a potential difference (voltage). The measured potential can be used to calculate the relative oxygen concentration on each side of the oxygen sensor.

   • Draw the Zr ions in the blank unit cell shown below.

   • Draw the oxygen ions in tetrahedral holes.

   • What % of the tetrahedral holes are occupied?

     

   • What is the charge in the Zr ion?

   • What is the charge on the oxygen ion?

   • What is the usual charge on Ca?

   • What has to happen to the number of oxygen ions to accommodate the replacement of Zr by Ca?

   • How many vacancies are there?

   • Explain how these vacancies allow oxide ions to move through the material.

   • Explain why electrons would be needed to convert oxygen into oxide ion.
   • Explain how, when the oxide turns back into oxygen, a current can flow from the platinum electrode on one side of the material, through a circuit and bac to the other platinum electrode.

3. Thermochromic Compounds

   Both Ag₂HgI₄ and Cu₂HgI₄ are thermochromic – they change colors at a certain temperature.

   The low temperature form (room temperature) of Cu₂HgI₄ is a bright red

   The high temperature form (> 55 °C) is a dark brown solid. This form is an ionic conductor which means that charge is carried by the new movement of ions. The Cu⁺¹ and Hg⁺² cations diffuse throughout the solid by hopping from tetrahedral site to tetrahedral site.

   

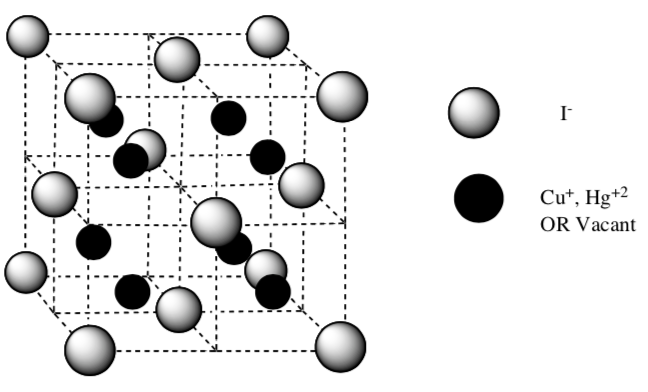
   • The structure has the Iodide ions filled as face centered cubic.

   • The cations (Cu⁺¹ and Hg⁺²) fill the tetrahedral holes in two adjacent cubic cells to provide a neutral compound with the correct molecular formula (Cu₂HgI₄).

     

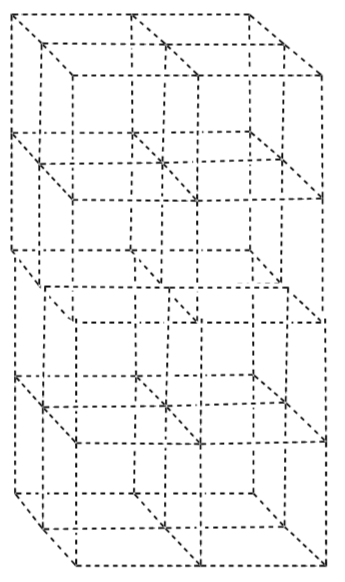
   • Why do the cations move, rather than the ions?

   • Which will be more likely to move Cu+1 or Hg+2?

   • Why is the height of this unit cell only half as large as for the low temperature?

4. Metallurgy in the Auto Industry

   The following illustration appeared in a newspaper article (New York Times: Science Times September 15, 2009) about innovation in the American steel industry. The article outlined efforts to make strong, lightweight steel for cars.

   

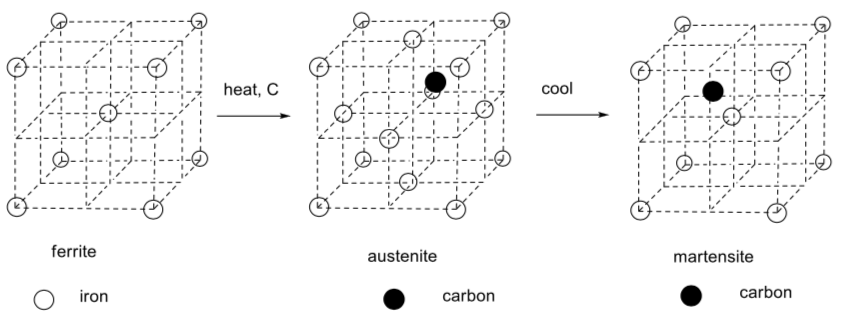
   Note the cool names for the two alloys, named after a famous British sports car maker.

   1. What is the packing system for the iron atoms in ferrite?

   2. Heating the ferrite in the presence of carbon leads to formation of austenite. What is the packing system for the iron atoms in austenite?

   3. What sort of coordination environment does the carbon occupy in austenite?

   4. What fraction of these holes are occupied?

   5. Given this unit cell, what is the ratio of carbon to iron in austenite?

   6. Careful cooling of the austenite leads to formation of martensite. How would you describe the coordination environment of the carbon in martensite?
      Note: This is not one of the three coordination geometries discussed. Describe it to the best of your ability.

   7. If the ratio of iron to carbon in a sample of martensite is 20:1, what does that tell you about the frequency with which carbon atoms occur in martensite unit cells?

   8. Why did the steelworkers introduce the carbon into the metal? What role does it play and how does it work?

   9. Compare the densities of austenite and martensite. The following space-filling diagrams may help. Assume the unit cells are the same size.

      

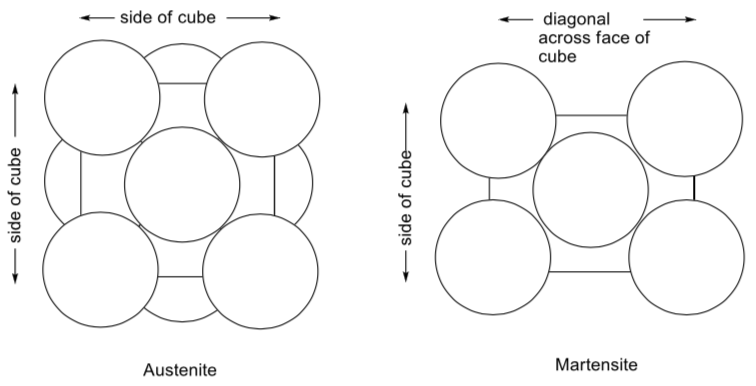
   10. Improved gas mileage is an increasingly important goal in car construction. Gas mileage will increase as density:

       increases decreases

   11. Which would be lighter weight leading to better gas mileage:

       austenite martensite

5. Superconductors

   A superconductor is a metal that loses electrical resistance at a cold temperature (T_c). Below the the Tc an electric current flows indefinitely without a loss of energy. Hg loses its resistance at 4.2 K. Scientists are looking for a substance that loses all resistance so that these materials could be used for power lines or electric trains without a loss of energy. This material was discovered to have a Tc at 90 K.

   This drawing is one unit cell for a superconducting material.

   • Complete the unit cell so that it is symmetric:

     • Add one entire Yttrium atom.

     • Add two Bariums atoms.

   • What is the empirical formula for this superconducting material?

   • There are two different CN for Cu. What are the two CN?

     

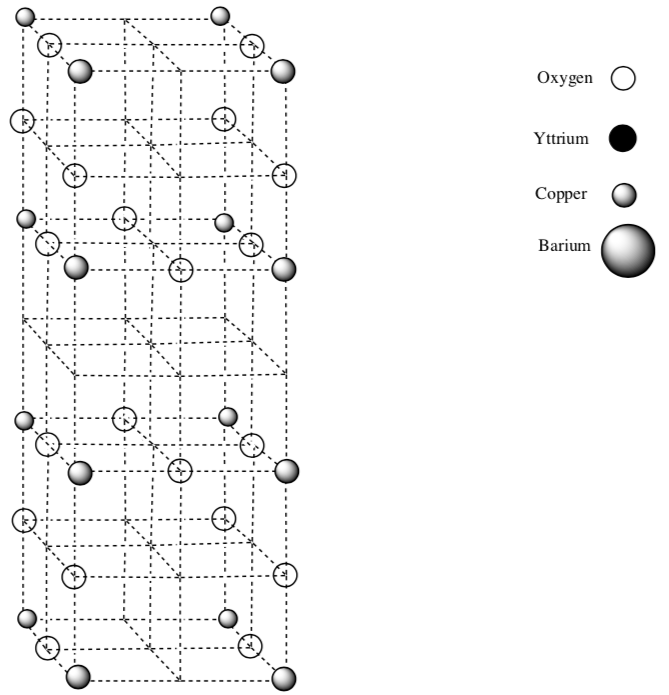
   • Propose a reason why this might conduct electricity well. (The answer is not well understood yet.)

Summarize using a Concept Map

Introduction to Concept Maps: http://www.msu.edu/~luckie/ctools/

Link also available on Sapling

Definition: Concept maps offer a method to represent information visually. There are a variety of such maps.

Purpose: Concept maps harness the power of our vision to understand complex information "at-a-glance." The primary function of the brain is to interpret incoming information to make meaning. It is easier for the brain to make meaning when information is presented in visual formats.

• Draw a Concept Map that ties these ideas together. Be sure to clarify how items are inter-related.

  • Atomic Size/Periodicityo

  • Ionic Radii/Periodicityo

  • Electronegativity

  • Face Centered Cubico

  • Simple Cubic

  • Body Centered Cubic

  • Hexagonal Closest Packedo Packing Efficiency

  • Coordination Number

  • Tetrahedral Hole

  • Octahedral Hole

  • Cubic Hole

  • Lattice Energy

  • Melting Point

  • Solubility

  • Malleability

  • Conductivity/Resistivity

  • Density

  • Coulomb’s Law

  • Charge Density