8. Metal Structures (Worksheet)
- Page ID
- 141682
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Structure of Solids Part I. Metals
Metal Packing
Metal solids consist of a regular array of atoms, molecules, or ions arranged in a repeating, infinite three-dimensional pattern – a lattice.
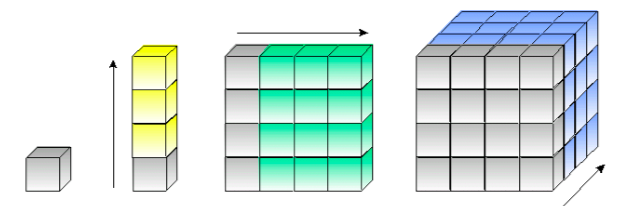
Base Layers (2D)
-
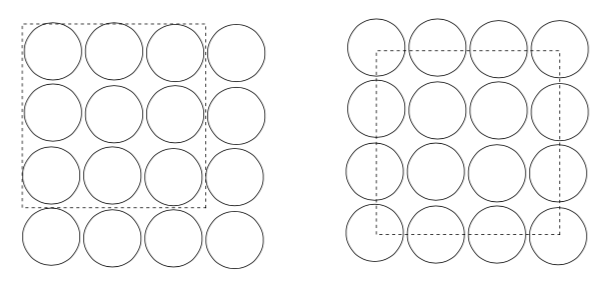
How many atoms fit into a square that is 3 spheres wide?
-
Does it matter where the box is drawn?
Stacking Cubic Layers
For metals, there are four common packing types, two have a cubic base.
-
Build a cubic base layer of spheres.
-
Place a second layer on top of it. There are two distinctly different ways the spheres in the second layer may sit with respect to the spheres in the first.
-
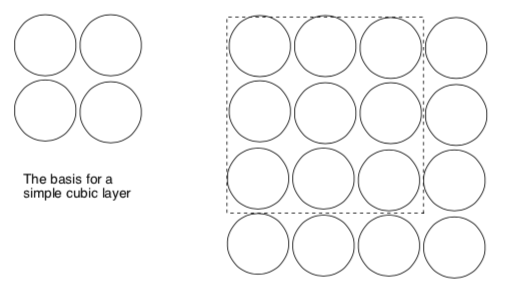
-
Draw these two possible 3D packing situations below. The cubic base layer is the basis for:
1 simple cubic a-a-a-a-a-a 2. body-centered cubic a-b-a-b-a-b
Identify the Unit Cell
The basic unit repeated throughout the structure is termed a unit cell. A unit cell must have 4 sides.
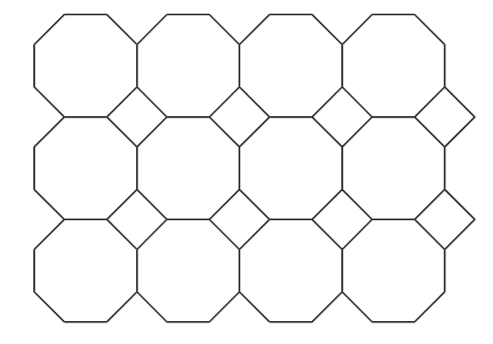
- Identify the smallest repeating pattern (ie unit cell) in this common bathroom tile pattern.
- Identify the smallest repeating pattern (ie unit cell).

More Practice finding a unit cell:
- Identify the smallest repeating pattern (ie unit cell). Remember the face of a unit cell must have 4 sides so you are looking for a cube.
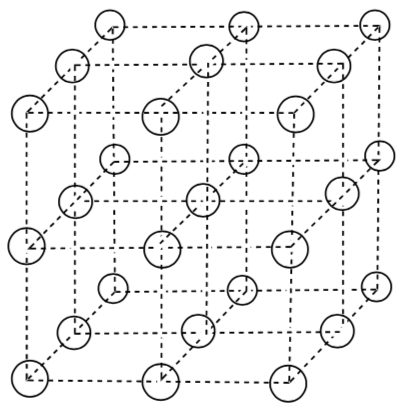
Unit Cell in 3D
A unit cell contains all of the structural and symmetry information to reproduce the packing of the lattice by stacking in 3D.
Below are two possible unit cells for the simple cubic packing.
- Does the unit cell on the left provide enough information to distinguish between simple cubic or body centered cubic packing? Explain.
- Does the unit cell on the right provide enough information to distinguish between simple cubic or body centered cubic packing? Explain.
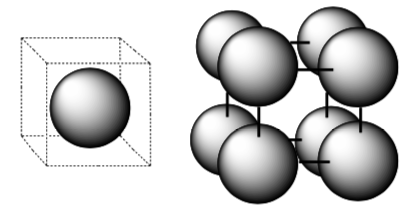
Two different types of unit cells:
-
Label the two types of cells (simple cubic or body centered cubic).
-
Determine the number of atoms in both of the unit cells shown above (how many atoms inside the box?). Show your work.
-
Assuming the box is the same size, which has more efficient packing (ie more atoms per unit cell)?
Hexagonal Layers (Closest Packed)
- Build a hexagonal base layer of spheres.
- Place a second layer on top of it. Where would they sit in order to pack most closely?
- Place a third layer on the second. There are two distinctly different ways the spheres may sit and still be as closely packed as possible.
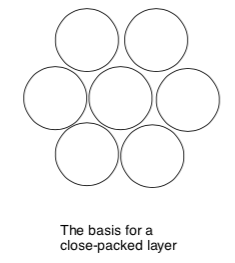
The hexagonal base layer is the basis for two more common packing types.
- Draw these two possible 3D packing situations below.
3. hexagonal closest packed a-b-a-b-a-b 4. cubic closest packed a-b-c-a-b-c (also called face-centered cubic)
Hexagonal Closest Packing Unit Cell
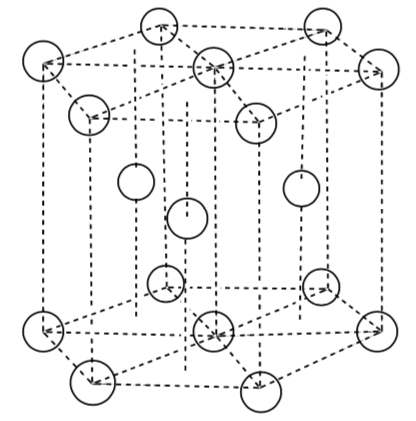
-
What packing system is shown here?
-
Indicate the layers (colored pencils help).
-
Place the atoms on the lattice below to make a unit cell of the system above. This unit cell looks like 1/3 of the pie/hexagon and is not cubic.

Face Centered Cubic Unit Cell
Two views of fcc packing:
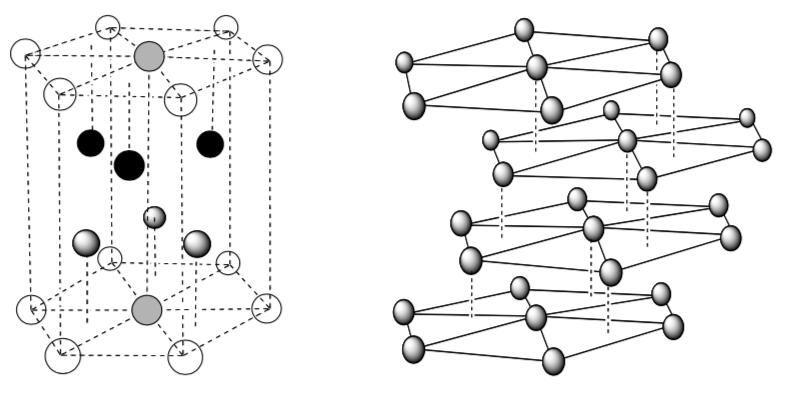
- Indicatethelayers(a–b–c–a)
A third view of fcc packing:
- Indicate the layers of the original hexagonal packing system (a – b – c – a ).
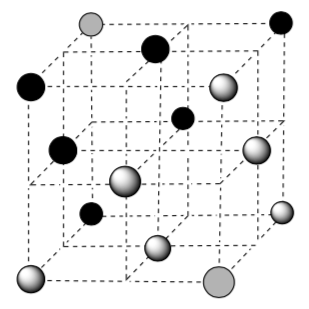
Closest Packing Unit Cells
-
How many atoms fit into a square that is 3 spheres wide?
-
Assuming the box above is the same as the box for the cubic base, which is more efficient:
Cubic Base Hexagonal Base
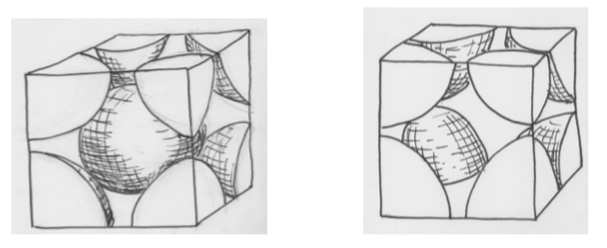
For the Face Centered Cubic Packing:
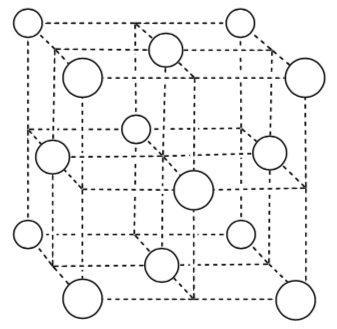
-
Calculate number of atoms in the unit cell.
-
Assuming the box is the same size as the cubic unit cell shown earlier, which has more efficient packing (i.e. more atoms per unit cell)?
Packing Efficiency
In earlier sections, you looked at the number of atoms/unit cell but this is not the best estimate of efficiency as the different cells are really different sizes.
More correctly, the packing efficiency is the volume occupied by the spheres in a unit cell divided by the total volume of the cell. It’s usually expressed as a percent.
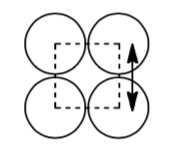
$$
\text { Packing Efficiency }=\frac{\text { Volume of spheres within a cube }}{\text { Volume of cube }} \times 100 \%
$$
Simple cubic
- Suppose the atoms each have a radius of 1 pm. Calculate the volume of the atom (V=4/3pr3). _______________
- Calculate the volume of the unit cell.____
- Now calculate the packing efficiency for the simple cubic structure.______.
| Structure | Packing efficiency (%) | Coordination number |
|---|---|---|
| Simple cubic | 6 | |
| Body-centered cubic | 68% | |
| Cubic closest packed | 74% | |
| Hexagonal closest packed | 74% | 12 |
Coordination Number
A second characteristic of a structure is the coordination number. For a metal, this is the number of atoms that touch any given atom.
- Now look at the pictures of the different packing schemes given previously, and complete the empty column by providing the coordination number for each structure.
Application Problems
-
Calculate the packing efficiency for the CCP (FCC) structure. (Hint-Use the figure in a previous part of the workbook to tally the number of atoms in the unit cell.)
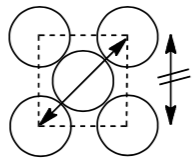
Notice that the atoms don’t touch along the edge of the cube but they do touch along the diagonal through the face of the cube.
-
Calculate the packing efficiency for the body-centered cubic structure. Show your work.
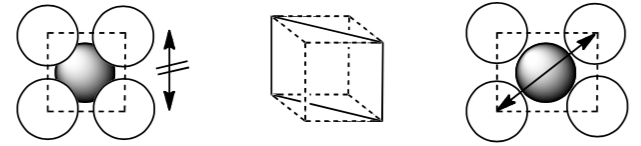
Notice that the atoms don’t touch along the edge of the cube but they do touch along the diagonal through the middle of the cube.
-
What is the relationship between packing efficiency and coordination number? Does this relationship make sense?
-
The density of a metal depends not only on the mass and volume of the individual atoms, but also the way they are packed in the solid state. Which of the four structures might you guess the most dense metals have? Explain.
-
Many metals are able to exist in two (or more) of the different structures, depending on the pressure exerted upon the sample. Indicate whether the following conversions should be favored, disfavored or unaffected by an increase in pressure. Explain your answer.
-
BCC -> SC
-
BCC -> HCP
-
FCC -> HCP
-
FCC -> SC
-
Summary
-
Draw a simple cubic unit cell. How many atoms are in one unit cell? What is the coordination number?
Number in Unit Cell:
Coordination Number:
-
Use the template below to draw a body-centered cubic unit cell. How many atoms are in one unit cell? What is the coordination number?
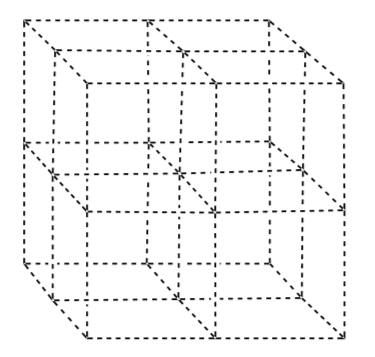
Number in Unit Cell:
Coordination Number:
-
Use the template below to draw a face-centered cubic unit cell. How many atoms are in one unit cell? What is the coordination number?

Number in Unit Cell:
Coordination Number:
Packing Practice
-
Iridium (Ir) metal packs in face-centered cubic packing (fcc).
-
Draw a base layer of spheres for fcc.
-
Show a top view of spheres for the first two layers of fcc together.
-
-
Tungsten (W) metal packs in a body-centered cubic (bcc) structure.
-
Draw a base layer of spheres for bcc.
-
Show a top view of spheres for the first two layers of bcc together.
-
Metal Properties: Activities
Properties of Metals: Station 1 (sea of electrons model)
Metals have unique characteristics such as the ability to conduct electricity, low ionization energies, and low electronegativities (so they will give up electrons easily to form cations).
Their physical properties include a lustrous (shiny) appearance, and they are malleable and ductile.
Model: In metal bonding, atoms are held together by delocalized bonds. Such bonds could be formed between metal atoms that have low electronegativities and do not attract their valence electrons strongly. This allows the outermost electrons to be shared by all the surrounding atoms, resulting in positive ions (cations) surrounded by a sea of electrons.

Conductivity
- Considering that electricity is the flow of electrons (or flow of charge) from one place to another, propose an explanation for why metals are generally good conductors of electricity, whereas solid ionic compounds are not.
Appearance
- Free electrons on the surface can bounce back light at the same frequency that the light hits the surface. This makes the metals appear _________.
Electronegativity
- Identify each material in the table as a metal or nonmetal.
Table 1. Classification of several materials composed of single elements listed in order of decreasing electronegativity, EN.
Material Metal/ nonmetal EN O2 3.61 N2 3.07 Cl2 2.87 H2 2.30 Cu 1.8 Al 1.61 Mg 1.29 Na 0.87 -
A metal is likely to have a:
Larger EN Smaller EN
-
Based on the sea of electrons model, why do you think that EN corresponds with metal/nonmetal nature of materials?
Thermal Conductivity
Metals are also known as being good conductors of heat, or thermal conductors. Heat is kinetic energy. In order for a substance to conduct heat, it must be able to transmit kinetic energy through vibration.
If heat is applied to one side of a piece of metal, then the nuclei will start to vibrate.
-
Based on the sea of electrons model, will the nuclei be able to vibrate freely?
-
Explain how the nuclei will transmit the energy to the rest of the metal.
-
In contrast, would a structure with strong rigid bonding be able to conduct thermal energy as easily?
-
Would you be more likely to be burned stirring hot soup with a metal spoon or a wooden spoon? Why?
Properties of Metals: Station 2 (box of marbles)
Activity:
Assume the metal is made of individual spheres. Place marbles in a box so that the box is approximately half full (but only one atom deep). Tilt the box away from you and then back toward you.
- What pattern, if any, do you notice?
Now, gently shake the box from side to side.
-
Draw the pattern that develops. How many nearest neighbors does each atom have? (Ignore exceptions to this on the edges.)
-
Do you notice any imperfections in packing?
Any significant sample of a real metal will contain a lot more atoms.
-
What do you think will be true about the number of imperfections in a real metal, as compared to these models?
-
What could you do to a metal to make the atoms pack more perfectly?
Properties of Metals: Station 3 (Plexiglas BB board)
Activity:
Assume the metal is made of individual spheres. Tilt the board away from you and then back toward you. Now gently shake it from side to side.
- What pattern develops? How many nearest neighbors does each atom have? (Ignore exceptions to this on the edges.)
Even within the interior of the BB board not all atoms arrange perfectly. Dislocationsare abrupt changes in the regular ordering of atoms, along a line (dislocation line) in the solid. They occur in high density and are very important in mechanical properties of material. A vacancy is a lattice position that is vacant because the atom is missing.
- Draw or describe a couple of the imperfections.
Using the BB board, one can vary the rate at which the container is shaken.
- Shaking of the BB atoms simulates _______________. (i.e. when do atoms start moving rapidly).
Materials are often stronger when they have defects.
- Suggest a reason why a metal might be harder or stronger when there are defects present.
Properties of Metals: Station 4 (Bubble Raft)
Activity:
Assume the metal is made of individual spheres. Use a pipette to blow bubbles below the surface of soapy water. Try to keep the bubbles uniform with a steady expulsion of air in deeper water, so tilt the container to one side and blow bubbles in the deep end. Once a “raft” of bubbles is created you can make the pan level again.
-
Draw the pattern that develops.
-
How many nearest neighbors does each atom have? (Ignore exceptions to this on the edges.)
-
Which type of base layer is this?
-
This model produces a common pattern of packing of atoms that is an important pattern in nature. Why?
Properties of Metals: Station 5 (paper clips)
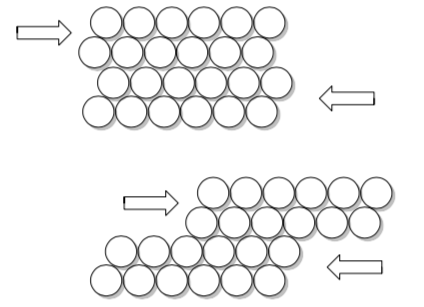
Activity: Ductility/Malleability
Metals are malleable (able to easily be bent or shaped into new forms. These activities will help determine what factors favor or disfavor atomic movement to adjust to a new shape.
Metals are ductile (can be pulled into long wires) and malleable (can be pounded into sheets) because the spheres can slide past each other in layers.
When a metal is subjected to a force, the nuclei can roll past each other on a cushion of electrons.
-
Take a paper clip, try to straighten it out and then try to bend it back into its original position. Describe what happens.
-
Take the paper clip and repeatedly bend it open and closed. What happens? Why did the metal lose its malleability?
- If we heated the paper clip and tried to reform the shape. What would happen? Would it be (more or less) malleable?
Heating a metal followed by rapid cooling is called hardening. (Knives are often treated in this way so they will stay sharp.)
- Explain why this treatment produces hardening.
Heating a metal followed by slow cooling is called annealing. (Wrought iron used in railings is treated in this way so that it can easily be bent or twisted into decorative shapes.)
- Explain why this treatment produces a soft metal.
-
Use the sea of electrons bonding model to explain the ductility and malleability of metals
-
Sodium is a very soft and malleable metal whereas magnesium is a harder metal.
-
Which one (Mg or Na) has more valence electrons? Mg or Na
-
Propose a reason why Na is soft and malleable and Mg is harder.
-
Properties of Metals: Station 6 (Marble Box with one larger marble)
Metals are malleable (able to easily be bent or shaped into new forms).
Activity: Alloys
Take the marble box with one larger marble to the box. Tilt the box away from you and then back toward you. Shake the box gently.
-
What do you notice about the regularity of the structure as compared to that of the “pure” metal?
-
What should this do to the malleability of the metal? Can you think of a real example of a material that would have this structure?
• Use these pictures to explain why bronze is more rigid.
One type of alloy is a partial or complete solid solution of one or more elements in a metallic matrix. In a “solid solution” one element replaces another while maintaining the same basic structure.
An alloy can have substantially different properties such as tensile strength and shear strength from those of the constituent materials.
For example, bronze is a metal alloy whose major component is copper, with tin between 4% and 12% by mass. Bronze is much less ductile than copper metal.
- Use these pictures to explain why bronze is more rigid.
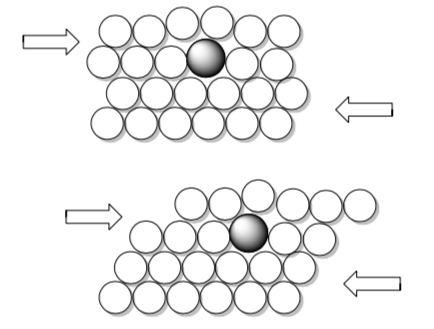
- The introduction of a non-metallic element into a metal will also cut down on malleability and ductility. Why? Consider how a non-metallic element will affect the sea of electrons.
Properties of Metals: Station 7 (bubble raft)
Activity: Ductility/Malleability of Metals vs Ionic Compounds
Blow a collection of uniform bubbles. Use a microscope slide to slowly push the raft into the wall of the container or into a second microscope slide. Do you see 1-2 atoms moving at a time or entire rows?
Metals are ductile (can be pulled into long wires) and malleable (can be pounded into sheets) because the spheres can slide past each other in layers.
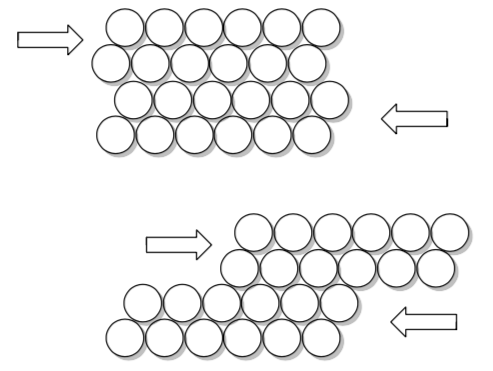
-
What happens if you hit a sheet of metal (your car door, for example) with a hammer?
-
Looking at this picture of an NaCl crystal with one plane of atoms shifting 1⁄2 of unit cell. Why doesn’t it want to slide like this?
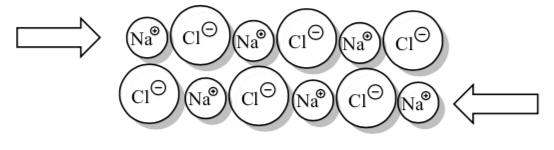
-
What happens if you hit a large salt crystal with a hammer?
-
Explain the difference in malleability between metals and ionic compounds. Use pictures to explain.
Summary
- Using the sea of electrons model, explain the properties of metals including alloys:
-
malleability
-
electrical conductivity/resistance
-
electronegativity
-
appearance
-
thermal conductivity
-
Application Problem
Part 1. Slip
Slip is the process by which an external force makes parts of the crystal lattice glide along each other, changing the material's geometry.
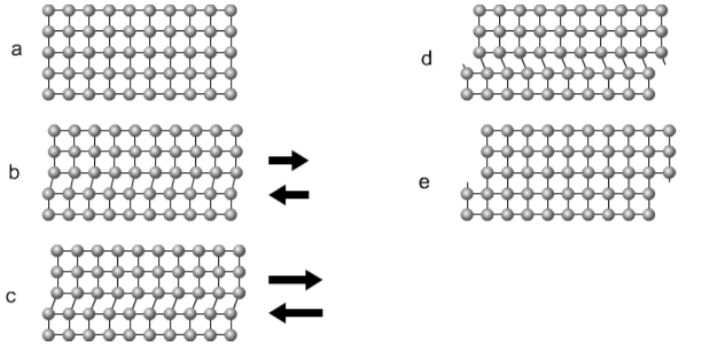
- Explain what is holding the metal atoms together to resist slip.
Part 2. Metal Properties and Shear Strength
Metals are often ductile.
- Define ductility.
Shear strength is a material's ability to resist forces that attempt to cause the internal structure of the material to slide against itself along a plane that is parallel to the direction of the force.
The ability to resist shearing is an important property of metals.
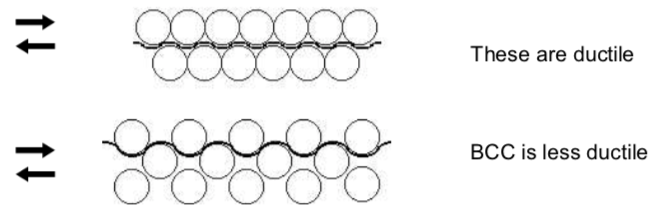
- Explain why bcc is more resistant to slip using the pictures above.
Part 3. Slip Planes
Ordinarily, there is a preferred plane (slip plane), and specific directions (slip direction) along which dislocations move. The direction and plane of the slip is dependent upon the metal packing system.
The {110} plane (highlighted below) is a common slip system in some metals. The atoms that are found on that plane are shown below.

- Predict which {110} plane will slip more easily:
FCC OR BCC
- Explain why that plane can slip easier.
-
Based on these slip systems, which metal packing would have a greater shear strength?
FCC OR BCC
Slip in hexagonal close packed (hcp) metals is much more limited than in bcc and fcc crystal structures.
- Draw a base layer for a metal in hcp.
Few active slip systems exist in hcp metals.
- Based on the packing structure, explain why there are few slip systems in this packing (in any directions).
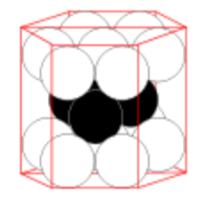
- The result of the small number of slip systems is that the hcp metal is generally
brittle OR ductile

