20: Hybrids and Conjugation

Hybridized Atomic Orbitals

Review Electronic Geometries

• Determine the electronic geometries of the following compounds:

  CH₄ CH₂CH₂ HCCH PF₅ SF₆

Review Bonding Motifs

• What combination of orbital overlap results in a double bond (π)?

• Draw a π bond.

• What combinations of orbitals overlap results in a single bond (σ)?

• Draw a σ bond.

In compounds that contain more than two atoms, it is common to refer to the geometries with a hybridization label. This label refers a mixing of atomic orbitals so that each atom is prepared to make bonds in the observed geometry.

• How many orbitals does each atom have?

• Does that match the number of orbitals in its valence shell?

• Does the number of orbitals match the number of bonds?

• Label the pictures of the orbitals in the table above with the type of bond each can make.

• Draw a picture of two sp² carbons forming ethene (CH₂CH₂) with 4 hydrogen atoms.

• Draw a picture of a carbon forming methane (CH₄) with 4 hydrogen atoms.

• Draw a picture of two sp carbons forming ethyne (HCCH).

Resonance and MO of Conjugated Systems

Examine the aligned p-orbitals below:

• What happens to the wavelengths of the electron in the orbitals above?

• As more atomic orbitals overlap, the number of bonding interactions

  increases OR decreases.

• As the bonding interactions increase, the energy of the new molecular orbital

  increases OR decreases

Electrons in orbitals that span three or more atoms are considered to bedelocalized and therefore more stable. This occurs in conjugated systems where there are 3 or more sp² hybridized atoms in a row (aligned p orbitals on each atom).

• Draw the p orbitals on each sp² hybridized atom in the structures below.

• Circle the atoms in each structure that are conjugated.

Atoms with a lone pair next to an sp2 atom are said to “rehybridize” to sp2 so that the conjugation is extended.

• Draw in the orbitals for the oxygen’s lone pairs.

• Which structure allows the oxygen lone pair to be in an orbital that is aligned with the π bond (conjugated)?

• Draw in the p orbitals.

• Circle the atoms in each structure that are conjugated.

Resonance Structures

A molecule with delocalized electrons often cannot be expressed by one single Lewis structure. The structure is represented by several contributing structures called resonance structures. A resonance hybrid is an average of the various Lewis structures.

The resonance structure should not be interpreted as a molecule switching between forms, but a molecule acting as an average of multiple forms.

Rules for Drawing Resonance Structures:

1. Total number of electrons must stay same.

2. All sigma (single) bonds MUST stay the same.

3. Net charge must stay the same.

4. Pi electrons(double or triple bonds)can move.

5. Nonbonding electrons can move.

It is easiest to draw a “template” of the single bonds and then add the extra electrons in various places.

• Draw the three best Lewis structures for pentadienyl anion, C₅H₇^- using the template below. You have 6 more electrons to add to each one.

• Calculate the charges.

• Draw the four best Lewis structures for phenoxide anion, C_cH₅O^- using the template below. You have 12 more electrons to add to each one.

• Calculate the charges.

More Practice with Resonance Structures:

• Draw resonance structures for the following compounds. Add any missing electrons.

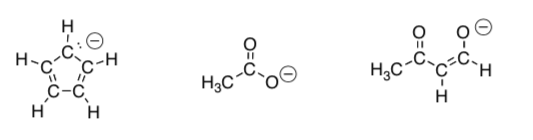
Practice Drawing Resonance

MO of Conjugated Systems

Developing MO diagrams for conjugated systems is similar to diatomic molecules. The rules stay the same.

1. There must be the same number of molecular orbitals as atomic orbitals.

2. There must be the same number of electrons in the molecule as in the atomic orbitals.

3. The overall combined energy of the molecular orbitals must equal the overall combined energy of the atomic orbitals.

For ethene (CH₂CH₂), MO diagram is shown below.

• Label the HOMO and LUMO.

The interesting properties of a molecule often come from the HOMO and LUMO π levels. So, in the interest of efficiency, chemists will often only draw the π orbitals for π and conjugated systems. This is called a Hückel MO diagram.

• Redraw the Hückel MO diagram for ethene (CH₂CH₂).

Hückel MO diagrams for increasingly conjugated systems:

Look for patterns:

• What happens to energy level (wavelength) of the lowest orbital as the conjugated system gets longer?

• What happens to energy level (wavelength) of highest orbital as the conjugated system gets longer?

• The number of energy levels for each compound is ___________to the number of p orbitals in each orbital picture.

• The number of pi electrons for each compound is equal to the _______ per pi bond and _______ per aligned lone pair and _______ per cation.

• How many nodes per each level? Is there a pattern to the number of nodes?

• In which structures are there non-bonding levels?

• How would the Hückel MO change if the allyl cation (CH₂CHCH₂⁺) were an allyl anion(CH₂CHCH₂^-)?

• Complete the Hückel MO energy diagrams for these conjugated systems:

  • Populate the MOs with the appropriate number of electrons

  • Fill in the missing pictures for any orbital energy listed

  • Indicate the highest occupied molecular orbital (HOMO)

  • Indicate the lowest unoccupied molecular orbital (LUMO)

  • Draw in the waves for each orbital and indicate the number of nodes for each orbital (frequency)

  • Count the bonding and anti-bonding interactions for each orbital combination and determine whether the orbital is overall bonding, anti-bonding or non-bonding.

These Hückel MO diagrams for conjugated systems are the same regardless of the type of atoms.

• Match these compounds with the correct MO diagram on the following page:

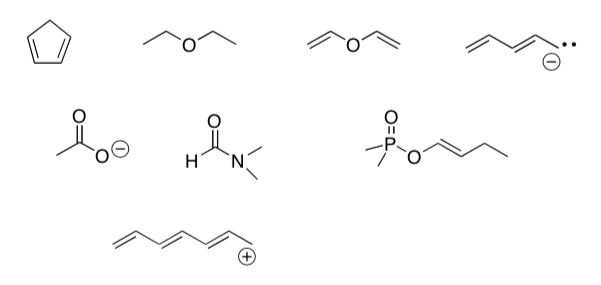
Appendix: Acyclic Molecular Orbital Patterns

Properties of Conjugated Systems

1. Rotational Barriers

   Murcko, Castejon and Wiberg, J. Phys. Chem. 1996, 100, 16162-16168.

   n-butane has a barrier to rotation about the C2-C3 bond of 3.45 kcal/mole whereas 1,3-butadiene has barrier to rotation of 6.7 kcal/mol – almost double that of butane.

   

   In order to explain the difference in rotational barriers, look at the Hückel MO diagram for 1,3-butadiene.

   

   • In butane, is the C2-C3 bond a single/double bond (circle one)?

   • In 1,3-butadiene, is the C2-C3 bond a single/double bond (circle one)??

   • Is the C2-C3 really a single bond?

   • Use the MO diagram to explain the rotational barrier observed.

   • Why is the s-cis higher in energy than the s-trans? [NOTE: This is not due to an MO effect]

2. Considering the conjugation, explain the following observations:

   1. Bond Lengths: The C2-C3 bond in 1,3 butadiene has a length of 148 pm which is 5 pm shorter than the length of the analogous single bond in butane.

      

   2. Stability: 1,3 –butadiene is 17 KJ/mol more stable than 1,4-pentadiene.

      

3. Reactivity

   Allyl systems are the shortest systems to be conjugated.

   

   The Hückel MO diagram for the allyl cation:

   

   • Using the MO diagram, where are the pi electrons in this compound?

   • Label the HOMO and LUMO orbitals.

   • If the allyl cation reacts with a nucleophile (a species with a lone pair) to form a new bond with the cation, which orbital is most likely to accept the electrons?

   The reaction below yields two products (shown). However, the constitutional isomer, 2-bromo-2-butene, is not observed.

   • Based on the MO diagram for the allyl cation,

     • Account for the two products that are formed

     • Explain why 2-bromo-2-butene is not formed

       

Summary

• Define conjugation.

• What are the rules for drawing resonance structures?

• What are the patterns in MO diagrams for conjugated systems?

• List how conjugation affects:

  • Rotational barriers

  • Stability

  • Bond lengths

Additional Problems

Problem 1:
Consider the following two compounds:

1. Draw resonance forms for the following two molecules if possible.

2. Using the Appendix of Acylic MO patters, draw Hückel Molecular Prbitals Diagrams for both of these molecules.

3. How do these MO diagrams differ?

4. What do the MO diagrams tell you about the geometry/free rotation of these two molecules?

Problem 2:

• Is cumulene (shown below) conjugated?

Problem 3:

Carbon Nanotubes

A carbon nanotube is a molecular structure that is best described as a rolled sheet of graphite with a large length to diameter ratio.

• Identify the molecular geometry of the carbon atoms in the structure.

• Identify the types of intermolecular forces present in the carbon nanotubes.

Highly polarizable pi-electrons (electrons in double bonds) transfer heat well, and single unit design of CNT allows efficient transfer of heat in a very tiny material. Currently carbon nanotubes are being explored to develop lightweight heat shielding materials.

• Why would a carbon nanotube be a good candidate for such an application?