19: Intro to MO
- Page ID
- 142914
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Molecular Orbital Theory
Molecular Orbital Theory is based on the ideas that electrons act as waves.
Review Concepts:
-
What is the relationship between frequency and wavelength?
-
What is the relationship between wavelength and energy?
-
Which wave:
-
has a higher frequency
-
has more intensity
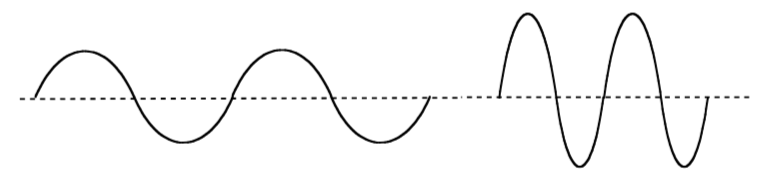
-
-
On these waves above, label and define a node.
-
What is different about the wave above the axis vs. below the axis?
-
Use shading to show the different phases on one of the waves above.
Physics Concepts:
-
What happens when two waves interact that are completely out of synch?

-
What happens when two waves interact that are partially in phase?

-
Thinking about waves, define:
Node:
Destructive Interference:
Constructive Interference:
Here is a picture of 2 s orbitals interacting in-phase:

-
Compare the wavelength of the electron in the atomic s orbital to the molecular s orbital.
-
What happens to the energy of this new overlapped orbital?

-
Show two s orbitals interacting out-of-phase.
-
Compare the wavelength of the electron in the atomic s orbital to the molecular s orbital.
-
What happens to the energy of this new overlapped orbital?
Orientation of p orbitals
Below, a standing wave is superimposed on the orbital drawing; this cartoon represents the wavelength of the electron in the p orbital.

There are three atomic p orbitals of the same energy. They are oriented in different regions of space.
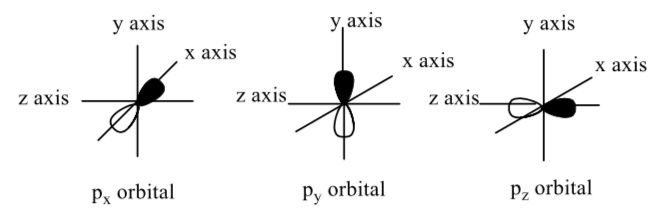
-
Using the sketches above, sketch the three p orbitals on a single atom.

Overlap of p orbitals
pz with pz The overlap of the pz orbital on the left atom with the pz orbital on the right atom is shown below:

-
Redraw these two orbitals (waves) on the axes below.

-
If these waves are interacting (overlapping), do you have constructive or destructive interference?
-
Show what happens to the wavelength of the electron in the combined orbitals above.
-
What happens to the energy of the electron? (increased or decreased)
This is called a sigma (σ) bond.
-
The overlap of two orbitals is considered a bond. Explain why bonding is favorable for molecules.
How will the situation change if the orbitals overlap as shown below?

-
Redraw these two orbitals (waves) on the axes below.

-
If these waves are interacting (overlapping), do you have constructive or destructive interference?
-
Show what happens to the wavelength of the electron in the combined orbitals above.
-
What happens to the energy of the electron? (increased or decreased)
This is called a sigma* (σ*) molecular orbital.
-
The overlap of two out-of-phase orbitals is considered an anti-bond. Is this a favorable interaction?
In-phase overlap of py with py
-
Draw the in-phase overlap of a py orbital on the left atom with a py orbital on the right atom.

-
If these waves are interacting (overlapping), do you have constructive or destructive interference?
-
Draw the wavelength of the electron in the new molecular orbital.
-
What happens to the energy of the electron? (increased or decreased)
-
What would the overlap of px with px look like?
This is called a pi ( \(\pi\) ) bond.
-
The overlap of two orbitals is considered a bond. Explain why bonding is favorable for molecules.
Out-of-phase overlap of py with py
-
Draw the out-of-phase overlap of a py orbital on the left atom with a py orbital on the right atom to make the pi* (\(\pi\)*) bond.
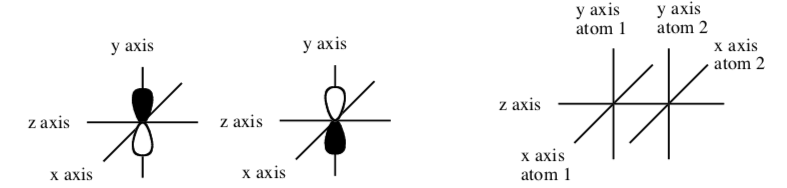
-
Show what happens to the wavelength of the electron in the combined orbitals above.
-
What happens to the energy of the electron? (increased or decreased)
Py with pz
-
Draw the overlap of a py orbital on the left atom with the pz orbital on the right atom.

-
Do these two orbitals overlap?
-
What happens to the wavelength of the electron? Is this a bond?
Comparison
-
Which type of interaction, s or p, creates the best overlap? Explain.
-
Label each of the orbital interactions below as either σ or \(\pi\).

Introduction to MO Summary
- Draw a picture to explain these statements. This is a way to employ “dual coding”. Dual coding is the idea that using both visual and verbal informationaids in learning. Evidence shows that memory for some verbal information is enhanced if a relevant visual is also presented or if the learner can imagine a visual image to go with the verbal information.
-
Molecular orbitals are are formed by the combination of atomic orbitals.
-
Orbitals can be combined in-phase or out-of-phase.
-
When two orbitals with the same phase combine, constructive interference occurs and electron density is concentrated between the nuclei. The wavelength of the electron is longer. This is lower energy and is considered to be a bond.
-
When two orbitals with the opposite phases combine, destructive interference occurs and electron density is diminished between the nuclei. The frequency of the electron increases. This forms an antibonding orbital and destabilizes the molecule.
-
Orbitals that interact "head on" (one orbitals directly "hits" another orbital) form σ (sigma) molucular molecular orbitals.
-
Orbitals that interact in a parallel fashion form π (pi) molecular orbitals.
-
Orbitals that are perpendicular cannot overlap and have no bonding or anti-bonding combinations.
-
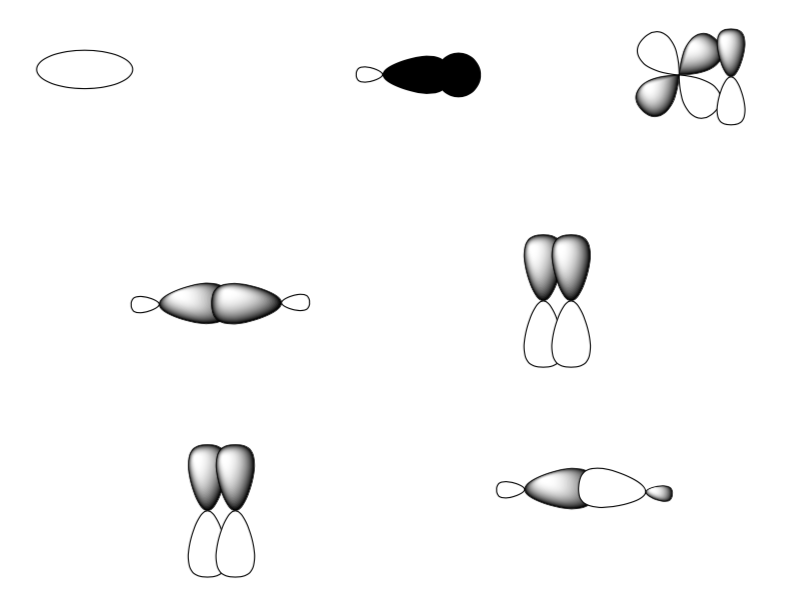
Bonding Summary
-
Which type of interaction, σ or π, creates the best overlap? Explain.
-
Label each of the orbital interactions below as either σ, σ*, π, or π*.
Rules for Orbital Diagrams
Electron filling is the same for MO diagrams as AO diagrams.
-
List the three rules for putting electrons into atomic orbitals.
Simple Rules for making Molecular Orbital Diagrams:
-
There must be the same number of molecular orbitals as atomic orbitals
-
There must be the same number of electrons in the molecule as in the atomic orbitals.
-
The overall combine energy of the molecular orbitals must equal the overall combined energy of the atomic orbitals.
Conventions used in MO interaction diagrams:
-
Atomic orbitals of the two atoms are placed on the left and right side of the page, with the molecular orbitals in the middle
-
The y-axis is energy.
Simple Diatomic Molecules
MOs for simple diatomic molecules can be constructed by combining the AOs from the two atoms. This is shown in the example below.
-
Fill in the electrons for the AOs and the MOs.

-
Based on your MO diagram, is H2 stable? In other words, do a majority of the electrons get longer wavelengths? (Bonding orbitals)
-
Construct an MO interactions diagram for He2.
-
Is He2 stable? In other words, do a majority of the electrons get longer wavelengths? (Bonding orbitals)
Molecular Orbital Diagram with p orbital interactions
Let’s construct the molecular orbital diagram for 
-
How many valence orbitals does nitrogen have?
-
How many ways can you combine the 2s orbital on N1 with the 2s orbital on N2? Draw them. (Hint: This should look like the H2 molecular orbital diagram).
-
Draw the in-phase interactions of the py of N1 with py of N2. Is this a [σ and π] bond? Circle one.

-
On the same coordinates, draw the in-phase interactions of px of N1 with px of N2. Is this a [σ and π] bond? Circle one.
-
Add the in-phase interaction of pz of N1 with pz of N2. Is this a [σ and π] bond? Circle one.
-
These three combinations could also be done out-of-phase. What kind of bond would result then?
When all of these possible orbital combinations are put together, a typical diatomic MO diagram is formed. Indicate which orbitals formed each level.
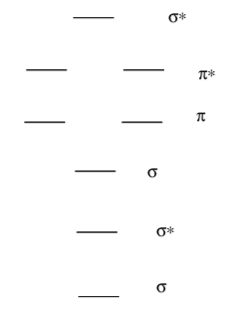
Bond Order
The complete diagram with p orbital interactions is shown below. Add the correct number of valence electrons for 

-
Calculate the bond order for the
 molecule.
molecule. Bond order = (number of bonding pairs – number of antibonding pairs) /2
-
Do the number of bonds in the Lewis structure of the N2 molecule match the bond order in the MO diagram?
More Practice
-
Draw Lewis structures of these compounds.
-
Fill in electrons for these diatomic MO diagrams and label all levels correctly.
-
Calculate the “bond order” for each diatomic molecule.


- Do these MO diagrams match the Lewis electron dot structures?
Additional Problems (MO diagrams of diatomics)
Problem 1:
-
Draw Lewis Dot Structure for carbon monoxide(CO).
-
Draw any resonance structures for this molecule.
-
A simplified Molecular Orbital Diagram for CO is shown below. Place the proper number of electrons in the diagram.

Using the MO diagram for CO, answer these questions.
Problem 2:
The electron configuration of O2 in MO terms is: (σ1s)2, (σ *1s)2, (σ2s)2,(σ*2s)2, (σ2p)2, (π 2p)2, (π 2p)2, (π*2p)1, (π*2p)1.
-
Draw the Lewis dot structure of molecular O2. How many unpaired electrons are in this structure?
-
Liquid molecular oxygen is visibly held in place between the poles of a strong magnet. Explain this in terms of the electron configuration.
-
Molecular O2 has a bond length of 0.121 nm while the molecule O2+ has a bond length of 0.112 nm and the oxygen anion, O2-, has a bond length of 0.126 nm. Explain the trend in bond lengths.
Problem 3:
The electron configuration of NO in MO terms is: (σ1s)2, (σ *1s)2, (σ2s)2,(σ*2s)2, (σ2p)2, (π 2p)2, (π*2p)1, (π*2p)1.
-
Draw the Lewis dot structure of molecular NO. How many unpaired electrons are in this structure?
-
Calculate the bond order for NO based on the electron configuration.
-
The bond length in NO is 0.115 nm while the bond length in NO+ is 0.1062nm. Calculate the bond order for NO+ and explain the change in bond length based on this difference.
Problem 4:
-
Propose a reasonable electroncon figuration in MO terms for BN.
-
Determine the bond order for BN.
-
Is BN diamagnetic or paramagnetic according to the electron configuration?

