13: Conformations (Workshop)

Molecular Structure: Acyclic Conformations

Conformational isomers are isomers that are formed by rotations about single bonds.

• Build a 3-D model of ethane (C2H6) using the model kits. Look at the following 2-D representations of the 3D structure of ethane.

  

• Build propane (C₃H₈) using the model kits.

• Add C and H atoms to show propane in in the following representations.

  

• Build butane (C₄H₁₀) using the model kits.

• Draw butane in:

  Wedge and Dash Representation Newman Projection

Conformational Analysis

Steric strain occurs when atoms are brought too close together. There is an associated cost in energy due to overlapping electron clouds.

• Circle sources of steric strain in these molecules.

• Calculate the increased energy due to steric strain. Each steric interaction increases the energy by 1 kcal/mole.

  

Torsional strain occurs when atoms separated by three bonds are placed in an eclipsed conformation instead of the more stable staggered conformation.

• Locate sources of torsional strain in these molecules.

• Calculate the increased energy due to torsional strain. Each eclipsed bond increases the energy by 1 kcal/mole.

  

Potential Energy Diagram of Rotation

At room temperature, the carbon-carbon bond of ethane is spinning rapidly. The following graph shows the Potential Energy of ethane in different conformations.

• Explain the difference in energy between the two conformations of ethane.

• Why are there only two conformations of ethane with different energy?

Potential Energy Diagram Practice

• Build a molecular model of 2–methylbutane.

• Complete the following Newman Projections for these six conformations.

• Calculate the amount of added energy from strain.

  

• Plot of energy versus angle of rotation around the C2–C3 bond.

  

Summary

• Define these types of isomers.

  • conformational isomers (often called conformers):

  • constitutional isomers:

  • stereoisomers:

• Clearly differentiate between these types of isomers.

• Define these types of strain.

  • Steric strain:

  • Torsional strain:

• Draw an example of the following conformations in a Newman Projection:

  • Anti:

  • Gauche:

  • Eclipsed:

Additional Problems:

1. Butane Conformational Analysis

   • Which of the following is the lowest-energy conformation of butane?

     

   • Which of the drawings represents the second most stable conformation of butane? (a local minimum)

     a) b) c) d)

   • Which of the drawings represents a conformation of butane in which torsion is maximized, but not sterics?

     a) b) c) d)

2. For this activity consider 1,2-diiodoethane:

   Here is the data from calculations on 1,2-diiodoethane:

   I-C-C-I dihedral angle	Energy (Kcal/mol)	Conformation description	Unfavorable interactions, if any.
   0°	12
   60°	0
   120°	4.5
   180°	0

   • Draw 1,2-diiodoethane.

   • Draw Newman projections for each of the 4 conformations.

   • Fill in the remaining column in the table above.

   • Fill in the graph below showing the energy of the conformations.

     

   • Why is there such a BIG energy difference between the conformation with a dihedral angle of 0° and 120°?

3. Acetylcholineisaneurotransmitteroftheautonomicnervoussystemthatsends information through the neurons to target organs. Most drugs that affect the nervous system tend to act at the synapse to alter chemical neurotransmission. The structure of ACh is drawn below. The structure is also drawn as N(Me)3⁺-CH₂-CH₂- OAc.

   

   1. DrawtheNewmanprojectionsforthedifferentconformationsobtainedthrough 60° bond rotations around the CH₂-CH₂ bond of this molecule. Label each

      conformation with the appropriate term such as gauche, etc.

   2. Draw an energy diagram for the complete rotation around this bond. Indicate which conformer is the most stable. Which conformer is the least stable?

   3. The two compounds below were synthesized and tested for cholinomimetic properties - that is tested for the production of a response resembling that of ACh. Isomer 1 had about the same activity as ACh; isomer 2 had about 1/500th of the potency of ACh. Which conformer of ACh must be the active form that binds to the receptor? Show Newman Projections to support your answer.

      

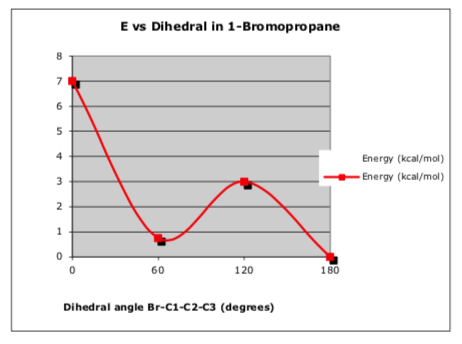
4. Conformational analysis of 1-bromopropane.

   • Draw 1-bromopropane.

The following graph represents strain energy vs. dihedral angle about the C1-C2 bond in 1-bromopropane.

• Use the data in this graph to determine a new set of steric and torsional strain energies that describes interactions in this molecule.

  

• Why is this basis set different from the one we used before?

• Draw 1-bromo-2-methylpropane.

• Apply your new set of energies to generate a plot of energy vs. dihedral angle in 1-bromo-2-methylpropane. Label with Newman projections and steric & torsional strain at each angle.

  

Molecular Structure: Conformations of Cyclohexane Structures

Cyclohexane – Chairs

The structure below is one way to draw the chair conformation. There are different types of H in this drawing, the “vertical” ones (axial) and “horizontal” ones (equatorial).

• Label each hydrogen on this structure as axial or equatorial.

  

Another way to define the types of H in this drawing is to determine if the C-H bond is point “up” or “down”. Extend the bond and see if it points up or down.

• Label each hydrogen on this structure as up or down.

  

Ring Flips

A ring flip is a phenomenon involving the interconversion (by rotation) around the C-C bonds of cyclic conformers.

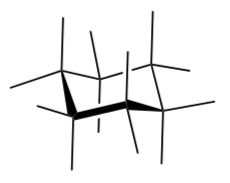
• Build methylcyclohexane. Position your model so that the CH3 group is equatorial.

• Add the CH3 and hydrogen atoms to the drawing for this conformer.

  

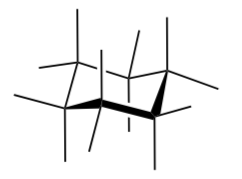
• Bend your model so that you have the CH3 group in an axial position.

• Add the CH3 and hydrogen atoms to the drawing for this conformer.

  

• Are the two conformers identical? Are there any types of strain apparent in one conformer that are not evident in the other?

• When cyclohexane undergoes a ring inversion:

  All axial substituents become ___________________.

  All equatorial substituents become ___________________.

  All up substituents stay ___________________.

  All down substituents stay ___________________.

Drawing Chair Conformations

It is important to draw chairs correctly in order to represent the 3D nature of cyclohexanes on paper.

Step 1: Everything is parallel lines. (If not parallel, then C is no longer tetrahedral)

all axial hydrogens are parallel

there are three other different sets of parallel lines

opposite bonds are always parallel

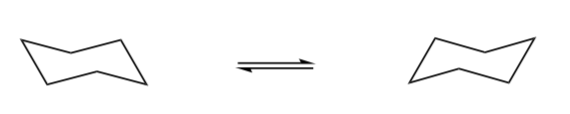
• Practice drawing some chairs.

• Add the hydrogens to these two chair conformers.

  

Step 2: Convert the structure from the cyclohexane to the chair conformers.

• Up means pointing above central plane.

• Down means the substituent points below the plane.

  

• Draw the TWO chair conformations of the following compounds.

  

Step 3: Ensure that the correct stereoisomer is depicted.

To get the correct stereochemistry, the substituents must be in the correct order around the ring AND in the correct Up/Down position.

• Draw the two chair conformations (with correct stereochemistry) of the following compounds:

  

Practice Stereochemistry on Chair Conformations

• Determine the relationships between the following pairs. Are they constitutional isomers, conformational isomers, enantiomers, diastereomers, identical or non- isomeric?

  

• 

Step 4: Draw the correct angles for bond angles of substituents.

Extended chairs have parallel lines that create the diamond lattice structures. Substituents and their bonds to hydrogens must fall on parallel lines also. This will be important as you attempt to determine steric strain.

Here is a correct drawing of methyl cyclohexane (with the methyl axial).

• Draw methyl cyclohexane with the methyl equatorial using the lattice below:

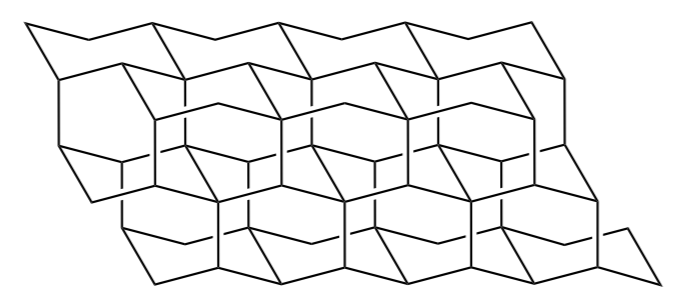
• Draw isopropyl cyclohexane with the isopropyl equatorial using the lattice below:

Step 5: Learn to draw the diamond lattice structure yourself.

diamond lattice is made of three distinct shapes

• Replicate these three structures using parallel lines
• Draw the diamond lattice
• Doodle these structures until you can reproduce them accurately

Calculating Strain in Chairs Conformations

When there is a substituent on a chair, there are two possible ring conformations. Chair conformations exist in equilibrium. Every substituent switches from axial to equatorial or vice versa.

To determine the most stable conformation, we need to assess the steric and torsional strain.

• What is the difference in steric strain between chair conformation of methylcyclohexane with the methyl axial vs the conformer with the methyl equatorial?

Practice Finding Steric Strain

• Find all the six atom interactions on the following structures. Use highlighters.

Practice Drawing and Calculating Steric Strain

1. Now consider cis-1,2-dimethylcyclohexane.

   1. Drawthetwopossiblechairconformers.

   2. Calculate the relative energy of each and determine which is the most stable.

2. Now consider trans-1,2-dimethylcyclohexane.

   1. Drawthetwopossiblechairconformers.

   2. Calculate the relative energy of each and determine which is the most stable.

3. Now consider cis-1,3-dimethylcyclohexane.

   1. Draw the two possible chair conformers.

   2. Calculate the relative energy of each and determine which is the most stable.

4. Now consider trans-1,3-dimethylcyclohexane.

   1. Draw the two possible chair conformers.

   2. Calculate the relative energy of each and determine which is the most stable.

5. Now consider cis-1,4-dimethylcyclohexane.

   1. Draw the two possible chair conformers.

   2. Calculate the relative energy of each and determine which is the most stable.

6. Now consider trans-1,4-dimethylcyclohexane.

   1. Draw the two possible chair conformers.

   2. Calculate the relative energy of each and determine which is the most stable.

Summary of Isomers:

• Draw a concept map to clearly identify the similarities and differences in isomers:

  Constitutional isomers, stereoisomers, R/S, enantiomers, diastereomers, meso, chiral center, chiral compounds, optically active, conformers, Newman Projections, etc.

Practice Multiple Choice

1. The most stable conformer of trans-2-methyl cyclohexanol is:

   

2. Which of the following structures is cis-1,2-dimethylcyclohexane?

   

3. Which of the following pairs are conformers of the same compound?

   

4. In which of these structures is the methyl group equatorial and the amine group axial?

   

Application Problems

1. The student looked up the structures in CSB stockroom inventory and found more than one entry for 1,3 cyclohexanediol shown below. (The “diol” portion of the name indicates that there are two OH groups attached to the ring.)

   

   • How many possible stereoisomers for 1,3 cyclohexanediol are there?

   • Draw 2 stereoisomers of 1,3 cyclohexanediol with wedges and dashes.

   • Draw these 2 stereoisomers of 1,3 cyclohexanediol as chairs.

   • What is the relationship of the two isomers above:

     enantiomers diastereomers conformers constitutional isomers

2. Two structures of glucose are shown below.

   

   • Draw the 2 chair conformers for \(\alpha\)-D-glucose. Circle the most stable chair.

   • Draw the 2 chair conformers for \(\beta\)-D-glucose. Circle the most stable chair.

   • How many chiral centers in glucose?

   • How many possible stereoisomers?

   • What is the relationship between \(\alpha\)-D-glucose and \(\beta\)-D-glucose?

     enantiomers diastereomers conformers constitutional isomers

   • Draw the mirror image of \(\alpha\)-D-glucose.

Calculation of Strain What does it mean?

From the energy differences, you can determine what percentage of both chair forms exist in a container of molecules.

In the interconversion of Chair1 ↔ Chair 2, an equilibrium (eq) constant, K_eq, is defined as:

$$
\mathrm{K}_{\mathrm{eq}}=[\text { Chair } 2] \mathrm{eq} /[\text { Chair } 1]_{\mathrm{eq}}
$$

where [Chair 2]_eq is the concentration of Chair 2at equilibrium (when the system has stabilized) and [Chair 1]_eq is the concentration of Chair 1 at equilibrium

$$
\Delta \mathrm{E}=\mathrm{E}_{\text { Chair } 2}-\mathrm{E}_{\text { Chair } 1}
$$

• What is the energy difference, ΔE, between the two chair forms of cyclohexane?

• Calculate the Keq for cyclohexane. K_eq =

• What is the energy difference, ΔE, for the interconversion of the two chair forms of cyclohexane (shown below):

  Chair 1 _AXIAL ↔ Chair 2 _EQUATORIAL ΔE = E2 _EQUATORIAL – E1 _AXIAL = ____________

• Which form (A or B) do you expect to be present at higher concentration at equilibrium? _____________

• Would you expect the K_eq to be ≈ 1, >1 or <1?

The K_eq can be calculated from the energy difference.

$$
\Delta \mathrm{E}_{\mathrm{eq}}==-\mathrm{RT} \ln \mathrm{K}_{\mathrm{eq}}
$$

where

R is a constant (1.99 x 10-3 kcal K−1mol−1
T is the temperature in Kelvin (Room Temp = 298 K)

Thus:

$$
\Delta \mathrm{E}(\mathrm{kcal} / \mathrm{mol})=-\mathrm{RT} \ln \mathrm{K}_{\mathrm{eq}} \approx-0.6 \ln \mathrm{K}_{\mathrm{eq}} \approx-1.4 \log \mathrm{K}_{\mathrm{eq}}
$$

• Complete the following table for Chair 1 _AXIAL ↔ Chair 2 _EQUATORIAL

  Keq	# Chair2/#Chair 1	% Chair 2	log Keq	ΔE (kcal/mol)
  0.001	1/1000
  0.01
  0.1
  1
  10
  100
  1000

• What is the size of the change in energy when the K_eq is increased by 10 fold?

• What happens to ΔE as K_eq increases?

• What happens to K_eq as ΔE becomes more positive?

• Now reverse the calculation and use ΔE values (which you can determine from atom interactions based on the diamond lattice).

  ΔE (kcal/mol)	Keq	# Chair2/#Chair 1	% Chair 2
  -4.2
  -2.8
  -1.4
  0
  +1.4
  +2.8
  +4.2

You might expect that different groups, depending on their size, might significantly affect the Keq values for the two chair forms.

• Using the method above, pick a couple examples below and calculate what percentage of the monosubstituted cyclohexanes are in the equatorial form.