13.5: Reversibility of the Coordinate Bond
- Page ID
- 140104
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A coordinate or dative bond is any covalent bond that arose because one atom brought a pair of its electrons and donated them to another.
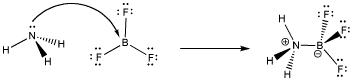
Figure AB5.1. Formation of a dative bond or coordinate bond between ammonia and boron trifluoride.
When the nitrogen donates a pair of electrons to share with the boron, the boron gains an octet. Both atoms are electronically saturated. In addition, a pair of non-bonding electrons becomes bonding; they are delocalized over two atoms and become lower in energy. This development acts as a driving force for formation of the dative bond.
- Formation of dative bonds can be driven by electronic saturation; that means octets become filled.
- Dative bond formation is also driven by the fact that bond formation allows nitrogen's lone pair to become delocalized.
However, sometimes bonds can be broken again. In the case of dative bonds, that means a pair of electrons that were donated from one atom to another can be taken back again. This event is called dissociation. In dissociation, two atoms that were connected to each other become disconnected.
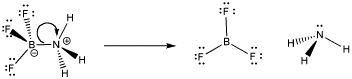
Figure AB5.2. Dissociation of a Lewis acid-base complex.
Why might a dative bond be broken? From one point of view, maybe the nitrogen atom's positive charge in the Lewis acid-base complex is unfavourable. Nitrogen is a relatively electronegative element, and so it is easy to imagine the nitrogen pulling this pair of electrons back to itself, leaving the boron behind without an octet.
There is another reason Lewis-acid complexes can dissociate. That reason is entropy, or the distribution of energy. One of the fundamental laws of thermodynamics is that increased entropy is favourable. Looked at very loosely, that means it is favourable to have energy distributed in more states or packages. One of the ways of accomplishing this goal is to divide the available energy up between multiple molecules.
Even though it costs energy to break the B-N bond in the Lewis acid-base complex, doing so can still be energetically favourable if that increased amount of energy can be distributed better between two molecules than it was in one molecule. Exactly how that energy distribution is accomplished is the subject of statistical mechanics, and is beyond the scope of this course. However, energy distribution is generally related to the ability of atoms to move. In molecules, that means it is related to the ability of bonds to stretch and compress, of bond angles to squeeze down and widen out, and for molecules to tumble and zip around. There are more ways to tumble and zip around if two molecules are doing it, rather than one. That means energy may be better distributed by two molecules than by one.
- Entropy factors favour the dissociation, or break-up, of Lewis acid-base complexes.
The fact that there is a good reason for Lewis acid-base complexes to form, and also a good reason for them not to form, may be very unsatisfying. However, it simply means that there is a balance between a nucleophile and electrophile coming together (association) and going apart (dissociation). Which direction the system will go depends on the relative importance of these two factors. The relative importance of each factor will vary from one case to another. In many cases, there is a dynamic equilibrium between the two possible cases. That means that after complexes form, they will come apart again. After complexes come apart, they will form again. This process does not stop, but continues as long as there is enough energy around to keep things moving.
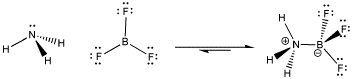
Figure AB5.3. The balance between the dissociated and associated compounds.
If it were possible to take a picture of a collection of molecules, the picture might show some of the molecules coordinated together and some of them wandering on their own. The ratio between the associated pairs and the dissociated molecules is related to the point of equilibrium. At the point of equilibrium, different factors driving the reaction to one side or the other balance each other out.
- Equilibrium is the balance between two possible states. For example, it is the balance between dissociated and associated ammonia and boron trifluoride.
In this case, the equilibrium heavily favours the Lewis acid-base complex. A picture of millions of ammonia and boron trifluoride molecules would show most of them coordinated together. A few molecules would be found on their own, however.
Problem AB5.1.
Use arrows and structures to show the dissociation of one nucleophile or Lewis base from each of the following polyatomic anions.
a) BF4- b) PF6- c) AlCl4- d) AlH4- e) Ag(NH3)2+
Problem AB5.2.
Draw pictures to represent the following cases of equilibria. Use squares to represent Lewis acids and circle to represent Lewis bases.
a) The Lewis acid-base complex is heavily favoured.
b) The Lewis acid-base complex is slightly favoured.
c) The Lewis acid-base complex is heavily disfavoured.
d) The Lewis acid-base complex does not form at all.
Sometimes, Lewis acid-base complexes are stabilized by chelation. Chelation (from the Greek word, chelos, meaning "crab") refers to the situation in which a Lewis base has more than one electron-donating site. That means it can bind to a Lewis acid through more than atom (just as a crab could grab something with both its claws).

Figure AB5.4. A general example of chelation.
The chelate effect refers to the fact that Lewis acid-base complexes are often more stable with respect to dissociation when they contain chelating electron donors. The equilibrium lies much farther towards the associated complex when chelation is a factor.
Chelation is seen in some very common biological molecules that incorporate Lewis acid-base complexes. For example, the heme subunit found in the oxygen-carrying proteins, hemoglobin and myoglobin, contains four electron-donating atoms that bind to iron. A very similar unit is found in a number of other molecules, including the important photosynthetic chromophore, chlorophyll. Related molecules are also found in the important biological cofactor, vitamin B12, and in cytochrome P450, which is involved in detoxification in the liver, among other tasks.
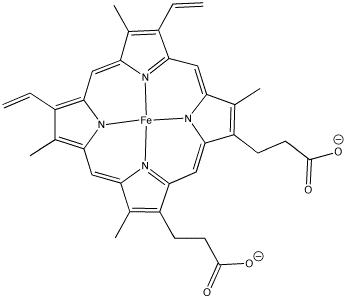
Figure AB5.5. The heme subunit of hemoglobin and myoglobin.
Problem AB5.3.
Using the concept of entropy, explain why an iron-heme complex is more stable than an iron ion complexed to four separate nitrogen donors, such as histidine or pyrrole anion.


