13.4b: Molecular Orbital Interactions in Lewis Acid-Base Reactions
- Page ID
- 140103
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Chemical reactions involve bond-making and bond-breaking events, as well as the movement of electrons. When we think about chemical reactions, we often think about where the electrons are coming from, and where they are going. In a Lewis structure picture, we most often think of the electrons as coming from a lone pair -- a non-bonding pair of electrons on one particular atom. We picture the electrons becoming attracted toward an atom that lacks electrons, maybe because it does not have a filled valence shell, or maybe because it has some amount of positive charge.
In addition to a Lewis picture, it's often useful to think about reactions in terms of molecular orbital interactions. That kind of consideration is especially useful in computational chemistry where, through the use of the right software, we can calculate energy changes that occur over the course of a reaction. It's also helpful to develop some conceptual understanding of these approaches qualitatively. This qualitative approach to molecular orbital interactions is routinely used by chemists because of the insight it can give into reactions.
One common way of thinking about reactions in this way is through the concept of frontier orbitals. This idea says that if one species is going to donate electrons to another in order to form a new bond, then the donated electrons are most likely going to come from the highest occupied energy level. In this level, called the highest occupied molecular orbital (HOMO), the electrons are further from the nucleus and therefore less tightly held by the protons in the nucleus. The electrons would be donated, in turn, to the lowest empty energy level on the other species, called the lowest unoccupied molecular orbital (LUMO).
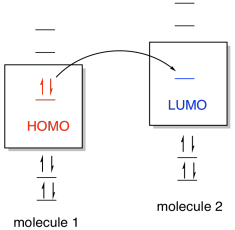
Figure AB4b.1. Molecular orbital interaction between frontier orbitals.
Consider an example of such an interaction, between a hydroxide ion and a proton. A hydroxide ion, HO-, is a Lewis base. The oxygen atom has three lone pairs, any of which might be donated to a Lewis acid. A proton, H+, is a Lewis acid. For a hydrogen atom, in the very first little row of the periodic table, the "octet rule" is two electrons, so a proton would be able to accept a pair of electrons from another atom and form a covalent bond.

The atomic orbital diagram for a proton is very simple. Hydrogen has only a 1s orbital, and in H+ that energy level is empty. This orbital corresponds to the LUMO for a proton.
The molecular orbital diagram for hydroxide ion is not much more complicated. This molecule is diatomic; it comes from the combination of an oxygen atom with a hydrogem atom, with the addition of an extra electron to provide the negative charge of the ion. In the diagram below, the hydrogen atom interacts with one of the p orbitals on the oxygen, but it doesn't matter exactly which oxygen orbital we use.
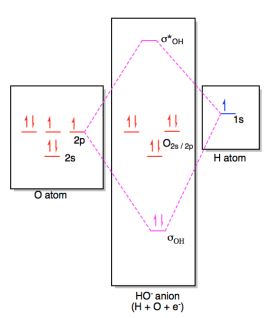
Figure AB4b.2. Molecular orbital interaction diagram for formation of hydroxide ion.
In most cases, we could come up with the MO diagram in another way. If we take the shortcut of working out an approximate MO diagram of a molecule based on its Lewis structure, and we know that hydroxide ion has one O-H bond and three lone pairs on oxygen, then we know there should be a bonding orbital at low energy, an antibonding orbital at high energy, and three non-bonding orbitals in the middle.
In a Lewis acid-base interaction, a pair of electrons would be donated from the non-bonding level on hydroxide (the HOMO) to the empty 1s orbital on the proton (the LUMO).
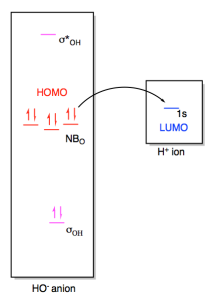
Figure AB4b.3. Frontier orbital interactions between a hydroxide ion and a proton.
What we have here is an interaction between two orbitals. A pair of electrons in one orbital is being shared with another orbital. We already know that an interaction between two orbitals results in two new orbitals. One of the new orbitals, resulting from constructive intereference, is lower in energy than either of the original orbitals. The other new orbital results from destructive interference and is higher in energy than either of the original orbitals.
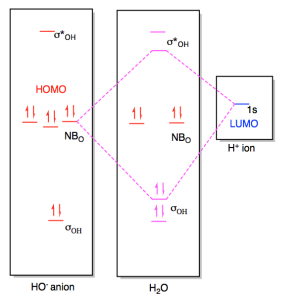
Figure AB4b.4. Frontier orbital interaction between a hydroxide ion and a proton, leading to the formation of a new bond.
In the end, the two electrons being donated slide down in energy to become an O-H bond. The combination that rises in energy doesn't really matter because there are no electrons at that level, anyway. Overall, the net energy of the proton and the hydroxide ion has decreased as the pair came together to form a water molecule.
Note that the MO diagram for the resulting water molecule resempbles what we would expect from its Lewis structure. There are two low-energy O-H bonding pairs and two correspondingly high-energy antibonding orbitals. There are also two intermediate-level nonbonding pairs corresponding to the two lone pairs we see in the Lewis structure.
We can use the same approach to look at Lewis acid-base interaction in bigger molecules. The MO diagrams are a little busier, but the ideas are the same. For example, we could imagine a fluoride ion donating electrons to a molecule of borane, BH3. The fluoride is a Lewis base because it has lone pairs. The borane is a Lewis acid because the boron atom lacks an octet; it has only six valence electrons in its structure.
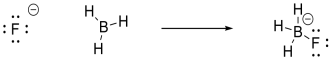
In this case, the borane contains three B-H bonds, so there will be three B-H bonding pairs and three empty B-H antibonding levels. There would be an empty orbital as well, corresponding to an empty p orbital on the boron. That empty p orbital is the lowest unoccupied molecular orbital (LUMO). A fluoride ion would have four lone pairs, and we would probably imagine a pair of electrons from one of its p orbitals as the highest occupied molecular orbital (HOMO). The interaction therefore involves donation from one of these orbitals on fluoride to the empty p orbital on borane.
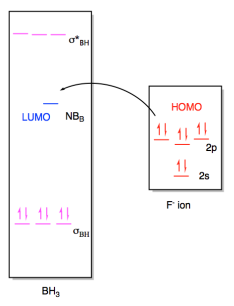
Figure AB4b.5. Frontier orbital interactions between a fluoride ion and borane.
Once again, this interaction would result in a new molecule with a new molecular orbital diagram. The only appreciable changes would involve the two orbitals that interact with each other, the HOMO and LUMO. The diagram for BH3F- ion is really a superposition of the two diagrams before, except that the HOMO and LUMO have formed a new bonding and antibonding orbital for the new B-F bond.
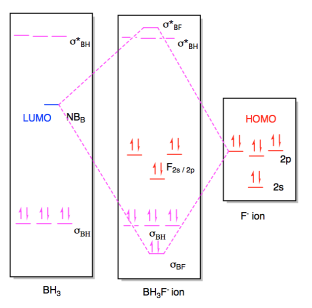
Figure AB4b.6. Molecular orbital interaction diagram for formation of an adduct between a fluoride ion and borane.
Problem AB4b.1.
For the following reactions, show (i) the HOMO-LUMO interaction and (ii) the molecular orbital interaction diagram for formation of the new molecule.
a) A fluoride ion donates to a boron trifluoride molecule (BF3), forming a tetrafluoroborate ion (BF4-).
b) An ammonia molecule (NH3) donates to a borane molecule (BH3), forming the adduct BH3NH3.

